Тема 6. Первообразная и неопределенный интеграл

Литература

1. Высшая математика для экономистов. Учебник / Под. ред. проф.

Н.Ш. Кремера. М.: ЮНИТИ, 1997, гл. 10 § 1- 4.

2. Карасев А.И., Аксютина З.М., Савельева Т.И.. Курс высшей математики для экономических вузов. М., 1982. Гл. 11. § 1- 6.

3. Пискунов Н.С. Дифференциальное и интегральное исчисление. М., 1985. Гл. 10. § 1- 4, 6.

В дифференциальном исчислении одной из основных задач является нахождение производной заданной функции. В интегральном исчислении ставится задача обратная: для заданной функции найти такую функцию F(x), производная которой равнялась бы заданной, т.е. Тогда функция F(x) называется первообразной функции f(x).

Множество всех первообразных функции называется неопределенным интегралом .

Таким образом, нахождение первообразной заданной функции является математической операцией, обратной дифференцированию функции.

Согласно этому утверждению, можно сформулировать основные правила интегрирования и записать таблицу неопределенных интегралов.

Правила интегрирования

1. Постоянный множитель можно выносить за знак неопределенного интеграла: .

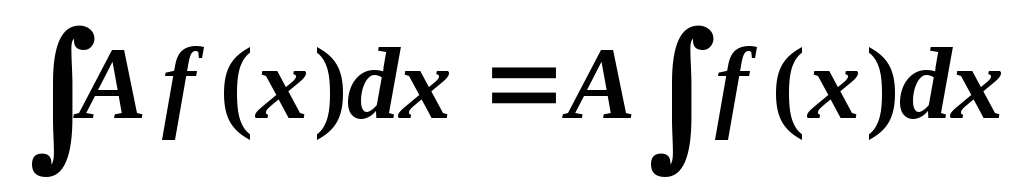2. Неопределенный интеграл алгебраической суммы двух или нескольких функций равен алгебраической сумме неопределенных интегралов этих функций:

.

Таблица неопределенных интегралов

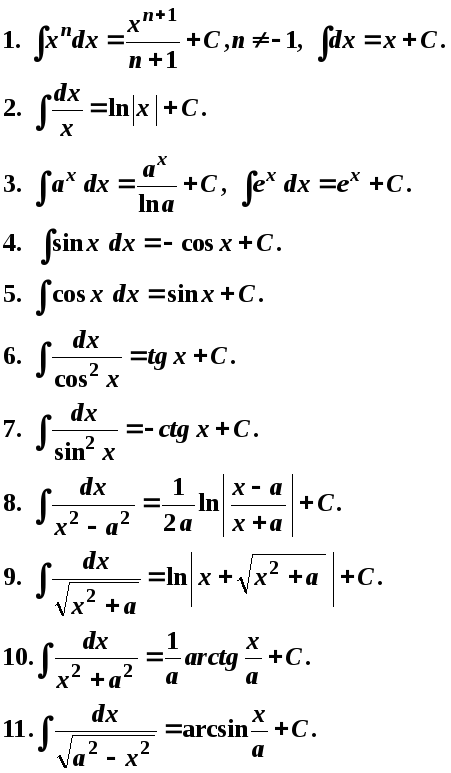
Различные методы интегрирования, которые рассмотрены далее, будут состоять в том, чтобы заданный интеграл с помощью некоторых приемов свести к табличным интегралам.

1. Метод непосредственного интегрирования

В основе этого метода лежит применение правил интегрирования и таблица интегралов.

Если подинтегральная функция представляет собой произведение или частное различных степеней х, то, выполняя необходимые действия, ее представляют как степенную функцию вида .

Например:

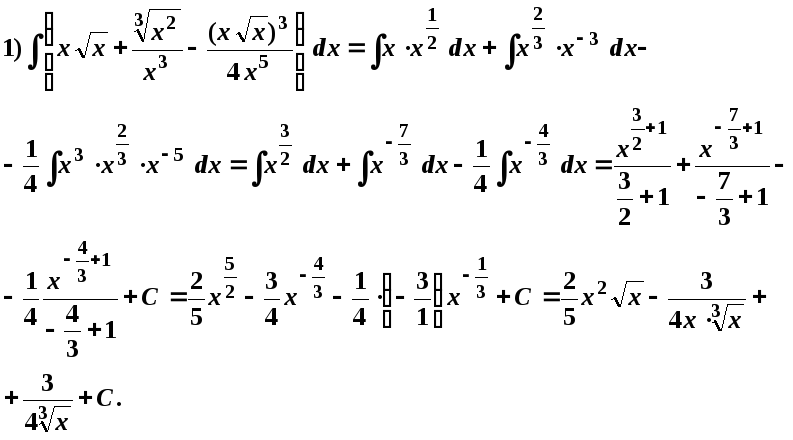
Проверим полученный результат, используя свойство неопределенного интеграла:

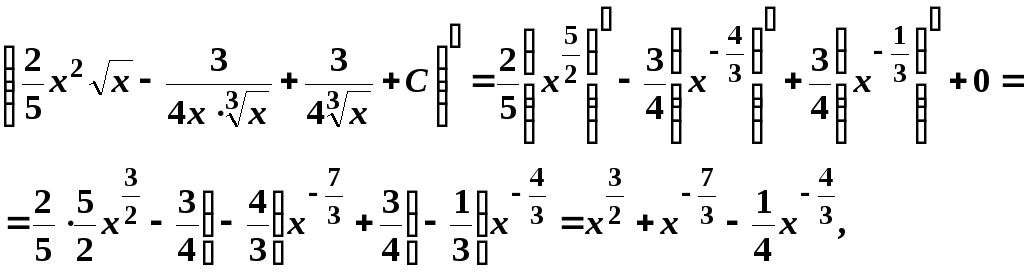
что равно подинтегральной функции.

Некоторые интегралы могут быть сведены к табличным после выполнения некоторых тождественных преобразований.

Например:

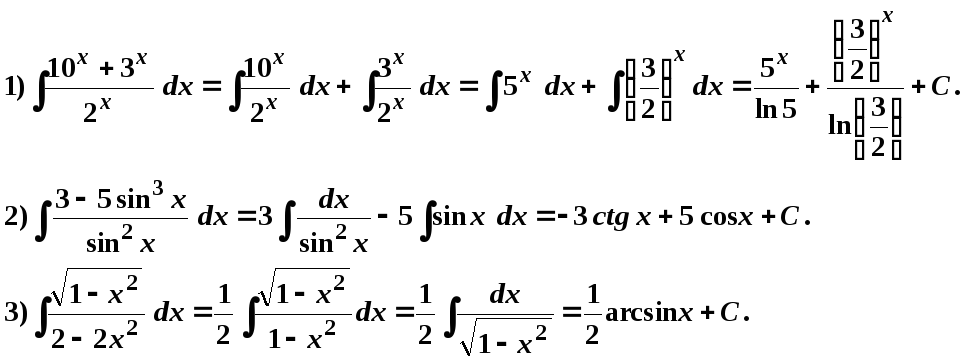
2. Метод замены переменной ( метод подстановки )

Метод подстановки является одним из наиболее мощных методов интегрирования. В основе метода лежит следующая формула: если , то интеграл

Убедиться в справедливости этой формулы можно, найдя производные от обеих частей равенства по переменной х и убедившись в равенстве этих производных.

Рассмотрим применение этой формулы на примерах:

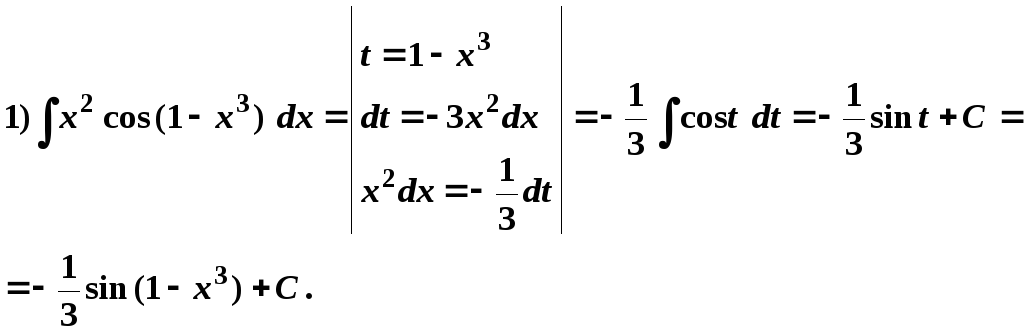
Проверим полученный результат, используя свойство неопределенного интеграла:

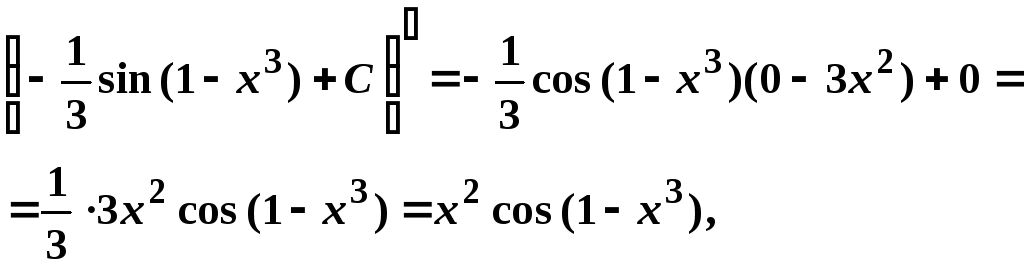
что равно подинтегральной функции.

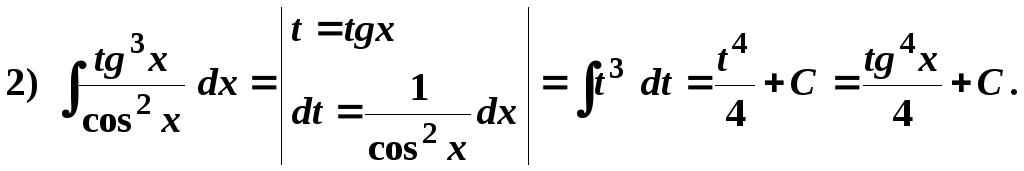
Проверим полученный результат:

что равно подинтегральной функции.

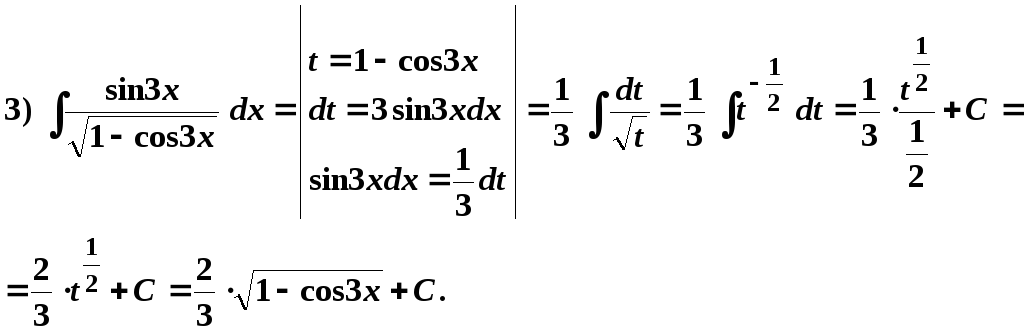
Проверим результат дифференцированием:

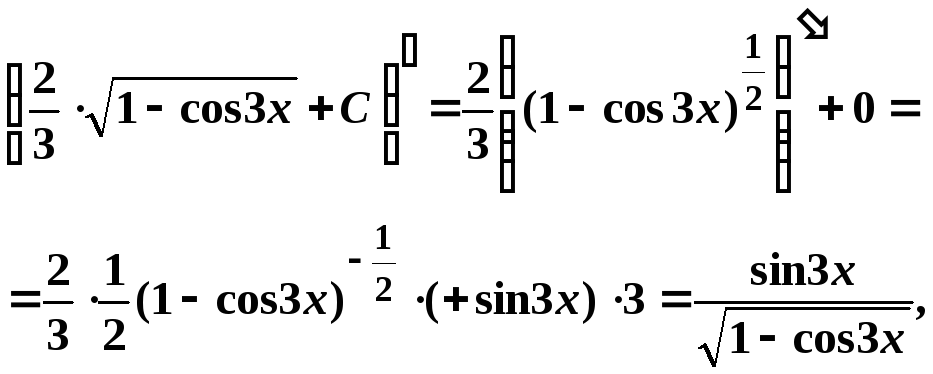
что равно подинтегральной функции.

3. Интегрирование по частям

Для вывода формулы интегрирования по частям будем исходить из формулы производной произведения двух функций и : Выразим и проинтегрируем полученное равенство почленно:

Поскольку интеграл , то получим выражение , которое называется формулой интегрирования по частям.

Практическая ценность формулы интегрирования по частям состоит в том, что она сводит вычисление интеграла к вычислению интеграла , который оказывается табличным или легко сводится к табличному.