Вариант 7

Задача 1. Приведите пример числового множества X , у которого:

1. ;

2. .

Имеет ли это множество X в случае а) и б) наименьший элемент?

Задача 2.

1. Используя определение предела числовой последовательности по Коши, доказать, что ;

2. Используя определение предела функции по Коши, доказать, что . Найти , если .

Задача3. Найти пределы:

1. ;

2. ;

3. ;

4. ;

5. .

Задача 4. Пользуясь методом замены бесконечно малых величин эквивалентными, найти .

Задача 5. Найти точки разрыва функции 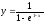и выяснить какого они рода.

Задача 6. Найти производные функций:

1. ;

2. ;

3. .

Задача 7. Найти вторую производную от функции, заданной параметрически .

Задача 8. Вычислить приближенно с помощью дифференциала .

Задача 9. Найти дифференциал второго порядка от функции

Задача 10. Провести полное исследование функции и на основании исследования схематически построить график функции:

1. ;

2. .

Вариант 8

Задача 1. Докажите, что множество [0;1]~[a;b], где a и b произвольные числа .

Задача 2.

1. Используя определение предела числовой последовательности по Коши, доказать, что ;

2. Используя определение предела функции по Коши, доказать, что . Найти , если .

Задача 3. Найти пределы:

1. ;

2. ;

3. ;

4. ;

5. .

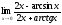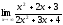Задача 4. Используя метод замены бесконечно малой величины эквивалентной, найти .

Задача 5. Найти точки разрыва функции и выяснить какого они рода.

Задача 6. Найти производные функций:

1. ;

2. ;

3. .

Задача 7. Найти вторую производную от функции, заданной параметрически .

Задача 8. Вычислить приближенно с помощью дифференциала .

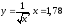Задача 9. Найти дифференциал второго порядка от функции .

Задача 10. Провести полное исследование функции и на основании исследования схематически построить график функции:

1. ;

2. .

Вариант 9

Задача 1. Покажите, что множество точек катета эквивалентно множеству точек гипотенузы.

Задача 2.

1. Используя определение предела числовой последовательности по Коши, доказать, что ;

2. Используя определение предела функции по Коши, доказать, что . Найти , если .

Задача 3. Вычислить пределы:

1. ;

2. ;

3. ;

4. ;

5. .

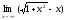Задача 4. Пользуясь методом замены бесконечно малых величин эквивалентными, найти .

Задача 5. Найти точки разрыва функции и выяснить какого они рода.

Задача 6. Найти производные функций:

1. ;

2. ;

3. .

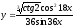Задача 7. Найти вторую производную от функции, заданной параметрически, т.е. найти .

Задача 8. Найти приближенно с помощью дифференциала .

Задача 9. Найти дифференциал второго порядка от функции .

Задача 10. Провести полное исследование функции и на основании исследования схематически построить график функции:

1. ;

2. .

Вариант 10

Задача 1. Найдите предельные точки этого множества, являются ли множество X замкнутым?

Задача 2.

1. Используя определение предела числовой последовательности по Коши, доказать, что ;

2. Пользуясь определением предела функции по Коши, доказать, что . Найти , если .

Задача 3. Вычислить пределы:

1. ;

2. ;

3. ;

4. ;

5. .

Задача 4. Пользуясь методом замены бесконечно малых величин эквивалентными, найти .

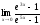Задача 5. Найти точки разрыва функции и выяснить какого они рода.

Задача 6. Найти производные функций:

1. ;

2. ;

3. .

Задача 7. Найти вторую производную от функции заданной параметрически .

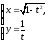Задача 8. Вычислить приближенно с помощью дифференциала .

Задача 9. Найти дифференциал второго порядка от функции .

Задача 10. Провести полное исследование функции и на основании исследования схематически построить график функции:

1. ;

2. .