МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

"ОРЕНБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ"

Г. А. ИВАШКИНА, А. А. КОВАЛЕНКО, Н.М. ВОРОТИЛОВА

Математический анализ

Задания к контрольным работам

для студентов специальности 010503 математическое обеспечение и администрирование информационных систем. Факультета дистанционного обучения.

I семестр

Оренбург 2007

Указания к выполнению контрольных работ.

При подготовке к выполнению контрольной работы студенту рекомендуется изучить теоретический материал, согласно программе и по указанной литературе.

Варианты контрольных работ распределяются по последней цифре зачетной книжки студента.

При выполнении контрольной работы и ее оформлении следует придерживаться следующих правил:

1. На титульном листе указать Ф. И. О. студента, его специальность и номер варианта.

2. Перед решением задачи необходимо записать полный текст ее условия.

3. Решение записывать аккуратно, соблюдая поля для замечаний рецензента.

4. Решение сопровождается четкими пояснениями.

5. Решение должно быть подробным.

Если в работе есть существенные ошибки, то она получает оценку "не зачет". В этом случае студенту следует выполнить работу над ошибками в той же тетради, в которой была решена контрольная работа.

В настоящем пособии решен нулевой вариант с пояснениями в помощь студенту.

Вариант 1

Задача 1. Доказать, что множество ограничено. Установить какие числа являются гранями. Найти точную верхнюю и точную нижнюю грани этого множества, а также наибольший и наименьший элементы множества.

Задача 2.

1. Используя определение предела числовой последовательности по Коши, доказать, что ;

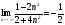2. используя определение предела функции по Коши, доказать, что 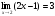. Найти , если .

Задача 3. Вычислить предел функции:

1. ;

2. ;

3. ;

4. ;

5. .

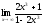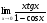Задача 4. Пользуясь методом замены бесконечно малых величин эквивалентными, найти .

Задача 5. Найти точки разрыва функции , выяснить какого они рода.

Задача 6. Найти производные функции

1. ;

2. ;

3. .

Задача 7. Найти вторую производную от функции, заданной параметрически .

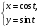Задача 8. Вычислить приближенно с помощью дифференциала .

Задача 9. Найти дифференциал второго порядка от функции .

Задача 10. Провести полное исследование функции и на основании исследования схематически построить график функции

1. ;

2. .

Вариант 2

Задача 1. Доказать, что множество ограничено. Установить какие числа являются его гранями. Найти точные верхнюю и нижнюю грани этого множества, а также наибольший и наименьший элементы множества

Задача 2.

1. Используя определение предела числовой последовательности по Коши, доказать, что ;

2. Используя определение предела функции по Коши, доказать, что . Найти , если .

Задача 3.Найти пределы:

1. ;

2. ;

3. ;

4. ;

5. .

Задача 4. Пользуясь методом замены бесконечно малых величин эквивалентными, найти .

Задача 5.Найти точки разрыва функции и выяснить какого они рода.

Задача 6. Найти производные функций

1. ;

2. ;

3. .

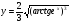Задача 7.Найти вторую производную от функции, заданной параметрически .

Задача 8. Вычислить приближенно с помощью дифференциала .

Задача 9. Найти дифференциал второго порядка от функции .

Задача 10. Провести полное исследование функции и на основе исследования схематически построить график функции

1. ;

2. .