
- •Акустический метод
- •Элементы теории упругости
- •Уравнения акустики
- •Упругие волны в однофазных горных породах
- •Упругие волны в многофазных горных породах
- •Методы решения прямой задачи скважинной акустики
- •Акустические волны в скважине Водные и поверхностные волны в скважине
- •Головные волны в скважине
- •Влияние неоднородности околоскважинного пространства на параметры головных волн
- •Заключение
Головные волны в скважине
Н
Рис.2. Механизм обра-зования головных
волн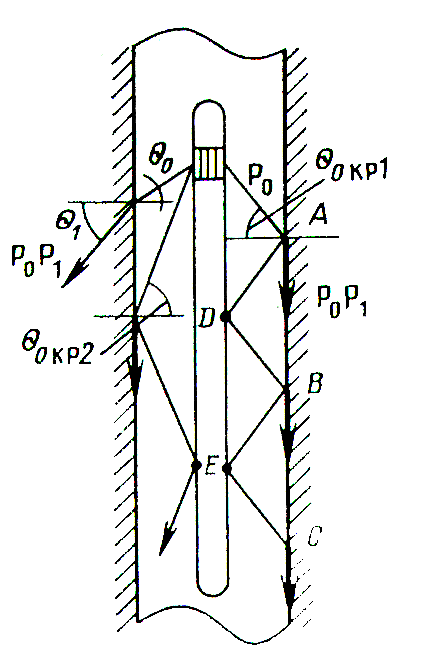
![]() на стенке скважины образуется преломленная
волна
на стенке скважины образуется преломленная
волна
![]() (рис. 2). Направления их волновых векторов
связаны законом Снеллиуса, являющимся
выражением принципа причинности, который
в данном случае можно сформулировать
как условие неразрывности фронтов
отраженной и преломленной волн. На
основе простых геометрических построений
не трудно показать, что если это условие
выполняется,
(рис. 2). Направления их волновых векторов
связаны законом Снеллиуса, являющимся
выражением принципа причинности, который
в данном случае можно сформулировать
как условие неразрывности фронтов
отраженной и преломленной волн. На
основе простых геометрических построений
не трудно показать, что если это условие
выполняется,
![]() .
Угол
.
Угол
![]() для которого
для которого
![]() (соответственно
(соответственно
![]() ),
называют первым критическим. При углах
падения
),
называют первым критическим. При углах
падения
![]() имеет место полное внутреннее отражение,
в связи, с чем возникают головные волны,
распространяющиеся вдоль границы
твердой и жидкой фаз со скоростью
имеет место полное внутреннее отражение,
в связи, с чем возникают головные волны,
распространяющиеся вдоль границы
твердой и жидкой фаз со скоростью
![]() продольной волны в породе. Учитывая
механизм образования, их, как и
преломленные, обозначают
продольной волны в породе. Учитывая
механизм образования, их, как и
преломленные, обозначают
![]() .
Очевидно, головная волна образуется,
если
.
Очевидно, головная волна образуется,
если
![]() .
.
П
Рис 3. Движение волны вдоль границы
твёрдой и жидкой фаз.
![]() больше скорости
больше скорости
![]() продольной волны в жидкости, в скважине
возникает вторичная продольная волна,
обозначаемая
продольной волны в жидкости, в скважине
возникает вторичная продольная волна,
обозначаемая
![]() .
Механизм ее образования можно пояснить
на основе принципа Гюйгенса — Френеля.
Для этого каждую точку стенки скважины,
например A, В, С, D
(рис. 3), следует считать источником волны
.
Механизм ее образования можно пояснить
на основе принципа Гюйгенса — Френеля.
Для этого каждую точку стенки скважины,
например A, В, С, D
(рис. 3), следует считать источником волны
![]() ,
возникающей в момент прохождения
через эту точку фронта волны
,
возникающей в момент прохождения
через эту точку фронта волны
![]() .
В изотропной среде, коей является
скважинная жидкость, такие парциальные
продольные волны будут сферическими,
так как они распространяются во все
стороны со скоростью
.
В изотропной среде, коей является
скважинная жидкость, такие парциальные
продольные волны будут сферическими,
так как они распространяются во все
стороны со скоростью
![]() .
Допустим, что фронт волны
.
Допустим, что фронт волны
![]() ,
движущейся со скоростью
,
движущейся со скоростью
![]() ,
находится в точке Е, а за t
секунд до этого находился в точке А.
Очевидно волна, излученная из А, к этому
времени представляет сферу радиусом
,
находится в точке Е, а за t
секунд до этого находился в точке А.
Очевидно волна, излученная из А, к этому
времени представляет сферу радиусом
![]() (окружности 1 на рис. 3, а и б). Аналогично
волны, излученные из точек В, С, D,
представляют сферы 2, 3, 4. По принципу
Гюйгенса парциальные волны гасят друг
друга в результате интерференции всюду,
за исключением их огибающей, которая
образует в скважине коническую
поверхность (линия 5 на рис. 3, а). Эта
волновая поверхность представляет
фронт волны
(окружности 1 на рис. 3, а и б). Аналогично
волны, излученные из точек В, С, D,
представляют сферы 2, 3, 4. По принципу
Гюйгенса парциальные волны гасят друг
друга в результате интерференции всюду,
за исключением их огибающей, которая
образует в скважине коническую
поверхность (линия 5 на рис. 3, а). Эта
волновая поверхность представляет
фронт волны
![]() .
Скорость движения волны в направлении,
перпендикулярном фронту, —
.
Скорость движения волны в направлении,
перпендикулярном фронту, —
![]() .
в направлении оси скважины —
.
в направлении оси скважины —
![]() .
Скорость
.
Скорость
![]() является, таким образом, кажущейся
скоростью волны
является, таким образом, кажущейся
скоростью волны
![]() ,
вдоль оси z. Поскольку
,
вдоль оси z. Поскольку
![]() фронт перемещается под критическим
углом к стенке скважины. Допустив, что
скорость в породе меньше чем в жидкости,
убеждаемся, что общая огибающая в этом
случае не возникает и волна в жидкости
не образуется (см. рис. 3, б).
фронт перемещается под критическим
углом к стенке скважины. Допустив, что
скорость в породе меньше чем в жидкости,
убеждаемся, что общая огибающая в этом
случае не возникает и волна в жидкости
не образуется (см. рис. 3, б).
Угол
![]() ,
для которого
,
для которого
![]() ,
называют вторым критическим. При
углах
,
называют вторым критическим. При
углах
![]() также
имеет место полное внутреннее
отражение, в связи, с чем в породе
возникают головные волны, распространяющиеся
вдоль границы твердой и жидкой фаз со
скоростью
также
имеет место полное внутреннее
отражение, в связи, с чем в породе
возникают головные волны, распространяющиеся
вдоль границы твердой и жидкой фаз со
скоростью
![]() поперечной волны в породе. Условие
образования головной волны в данном
случае
поперечной волны в породе. Условие
образования головной волны в данном
случае
![]() .
Эта волна также образует продольную
волну в жидкости, обозначаемую
.
Эта волна также образует продольную
волну в жидкости, обозначаемую
![]() .
Ее конический фронт перемещается вдоль
оси скважины со скоростью
.
Ее конический фронт перемещается вдоль
оси скважины со скоростью
![]() .
.
Поскольку в волне
![]() энергия перераспределяется между
волнами одного типа — продольными —
эту волну называют монотипной головной.
Соответственно волну
энергия перераспределяется между
волнами одного типа — продольными —
эту волну называют монотипной головной.
Соответственно волну
![]() называют обменной головной.
называют обменной головной.
Головные волны
![]() и
и
![]() являются неоднородными: их амплитуды
при
являются неоднородными: их амплитуды
при
![]() уменьшаются с увеличением r.
Уменьшение амплитуд тем интенсивнее,
чем больше угол
уменьшаются с увеличением r.
Уменьшение амплитуд тем интенсивнее,
чем больше угол
![]() ,
при котором возникла головная волна.
Поэтому коэффициент передачи энергии
в головную волну максимален вблизи
,
при котором возникла головная волна.
Поэтому коэффициент передачи энергии
в головную волну максимален вблизи
![]() .
Условно можно считать, что в кольцевом
зазоре «прибор — стенка скважины» волна
.
Условно можно считать, что в кольцевом
зазоре «прибор — стенка скважины» волна
![]() образуется не во всех точках закритической
области (
образуется не во всех точках закритической
области (![]() ),
а дискретно в точках А, В, С и т. д. (см.
рис. 2), расположенных, как нетрудно
видеть, на расстоянии
),
а дискретно в точках А, В, С и т. д. (см.
рис. 2), расположенных, как нетрудно
видеть, на расстоянии
![]() одна от другой. Интерференцией этих
волн (их «пристраиванием» одна к другой)
объясняется вид головной монотипной
волны, регистрируемой в скважине.
Действительно, форма головной волны
должна, казалось бы, повторять форму
излученного импульса, имеющего 1,5—2
периода. Однако ее реальная форма
представляет собой цуг колебаний, число
периодов в котором существенно больше.
одна от другой. Интерференцией этих
волн (их «пристраиванием» одна к другой)
объясняется вид головной монотипной
волны, регистрируемой в скважине.
Действительно, форма головной волны
должна, казалось бы, повторять форму
излученного импульса, имеющего 1,5—2
периода. Однако ее реальная форма
представляет собой цуг колебаний, число
периодов в котором существенно больше.
Вследствие интерференции распределение
энергии в спектре зарегистрированных
колебаний отличается от ее распределения
в спектре излученных колебаний.
Подчеркиваются те частоты, для которых
интерференция происходит в фазе, иными
словами, для которых на участках ADB,
ВЕС (см. рис. 2) укладывается целое число
волн. Это явление называют конструктивной
интерференцией. Поскольку отрезок
АD для волны
![]() меньше соответствующего отрезка для
волны
меньше соответствующего отрезка для
волны
![]() ,
видимая частота обменной волны меньше,
чем монотипной.
,
видимая частота обменной волны меньше,
чем монотипной.
В общем случае видимая частота соответствует наименьшей частоте конструктивной интерференции. Определим ее.
В ремя
распространения волны
ремя
распространения волны
![]() на участке АDВ равно
на участке АDВ равно
![]() .
Время прохождения волной
.
Время прохождения волной
![]() участка АВ равно
участка АВ равно
![]() .
Интерференция в фазе возникает, если
разность этих времен кратна периоду.
Отсюда, учитывая, что
.
Интерференция в фазе возникает, если
разность этих времен кратна периоду.
Отсюда, учитывая, что
![]() ,
получаем
,
получаем

Г
Рис. 4. Положение фронтов упругих волн
в моменты времени
![]() и
и
![]()
![]() целое число,
целое число,
![]() — частота волны, испытавшей конструктивную
интерференцию. Видимая частота волны
— частота волны, испытавшей конструктивную
интерференцию. Видимая частота волны
![]() соответствует
соответствует
![]() .
.
Видимую частоту волны
![]() определяют аналогичным образом.
определяют аналогичным образом.
В реальных условиях диаметр скважины меняется, а прибор отклоняется от оси. Поэтому распределение энергии в спектре зарегистрированных колебаний, в известной степени, случайная величина и спектральный анализ сигналов с целью определения параметров пород целесообразно проводить по начальной части волновой картины, которая не осложнена конструктивной интерференцией.
При распространении головных волн вдоль
стенки скважины они затухают за счет
расхождения и поглощения. На низких
частотах расхождение монотипной волны
пропорционально
![]() а
обменной —
а
обменной —
![]() ,
где
,
где
![]() — расстояние, пройденное в породе. Если
оно учтено, затухание можно считать
функцией только параметров среды.
— расстояние, пройденное в породе. Если
оно учтено, затухание можно считать
функцией только параметров среды.
Интерференция волн затрудняет, а иногда делает невозможной их идентификацию.
Рассмотрим в лучевом приближении
положение фронтов прямых
![]() ,
отраженных
,
отраженных
![]() и монотипных
и монотипных
![]() волн в скважине в моменты времени
волн в скважине в моменты времени
![]() и
и
![]() (рис. 4).
(рис. 4).
Допустим в момент времени t
= 0 излучен импульс упругих колебаний,
а в момент
![]() головная волна
головная волна
![]() впервые достигла оси z
скважины в точке В, расположенной на
расстоянии
впервые достигла оси z
скважины в точке В, расположенной на
расстоянии
![]() от источника излучения А. Одновременно
с ней достиг точки В и фронт отраженной
волны
от источника излучения А. Одновременно
с ней достиг точки В и фронт отраженной
волны
![]() ,
который может быть построен с помощью
мнимого источника А'. Прямая волна
,
который может быть построен с помощью
мнимого источника А'. Прямая волна
![]() к этому моменту обгоняет фронт головной
волны на величину отрезка ВС. Однако
фронт волны
к этому моменту обгоняет фронт головной
волны на величину отрезка ВС. Однако
фронт волны
![]() движется вдоль оси z
со скоростью большей, чем фронт волны
движется вдоль оси z
со скоростью большей, чем фронт волны
![]() .
Поэтому к некоторому времени
.
Поэтому к некоторому времени
![]() он обгоняет его на величину отрезка DЕ.
Очевидно, что
он обгоняет его на величину отрезка DЕ.
Очевидно, что
![]() .
.
Время прихода волны
![]() в точку В
в точку В
![]() .
.
Время прихода головной волны в точку,
расположенную на расстоянии длины зонда
![]() от источника
от источника
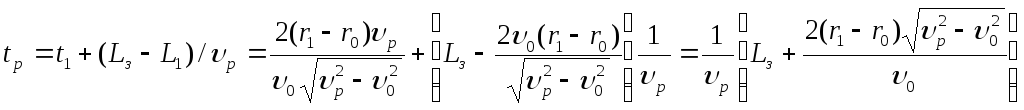 (3.9)
(3.9)
Зависимость времени прихода волны от
расстояния
![]() между излучателем и приемником называют
годографом этой волны. Выражение
(3.9)—уравнение годографа монотипной
волны. Для прямой волны уравнение
годографа имеет вид
между излучателем и приемником называют
годографом этой волны. Выражение
(3.9)—уравнение годографа монотипной
волны. Для прямой волны уравнение
годографа имеет вид
![]() .
(3.10)
.
(3.10)
Сопоставление выражений (3.9) и (3.10) показывает, что при
![]() (3.11)
(3.11)
монотипная волна обгоняет прямую.
Аналогично можно найти годограф обменной волны и определить расстояние, при котором ее удастся зарегистрировать раньше, чем возникнет интерференция с прямой волной.
Таким образом, существует принципиальная возможность регистрации не осложненных интерференцией головных волн в скважине. Их параметры характеризуют упругие свойства среды за стенкой скважины.
