21

Акустический метод

Одним из ведущих методов изучения разрезов скважин является акустический метод, основанный на измерения параметров упругого волнового поля в скважине. Метод предназначен для непосредственного изучения акустических параметров волнового поля горных пород пересечённых скважиной. Акустические параметры горных пород функционально связаны с физико-механическими свойствами, пористостью, структурными особенностями и характером насыщения. В обсаженных скважинах характеристики акустических сигналов также тесно связаны с условиями передачи упругих деформаций на границе цементного кольца с породой и с колонной. Эти обстоятельства создают предпосылки для эффективного применения этих зависимостей для решения широкого круга геофизических задач.

В лекции описаны основные уравнения акустического метода, а также даны характеристики основных видов волн, возникающих в скважине и околоскважинном пространстве.

Элементы теории упругости

Действие внешних сил на тела, находящиеся в равновесии, компенсируют внутренние упругие силы, порождающие в телах упругие напряжения.

Выделим в среде малый объем , а в нем — площадку dS. Если на нее действует произвольно направленная сила dF, вектор напряжения на площадке

, (1.1)

где индекс n указывает направление, нормальное к площадке. На площадках, перпендикулярных координатным осям , , в этом случае согласно формуле (1.1) действуют вектора напряжений , , . Разложив вектор на составляющие, получим , , . Очевидно, что — напряжение нор­мальное к площадке, перпендикулярной оси ; и — на­пряжения, касательные к ней и направленные по осям , соответственно. Разложив аналогично и , получим девять составляющих, полностью характеризующих напряжения в данном точке среды и именуемые тензором напряжений σ. В координатном форме

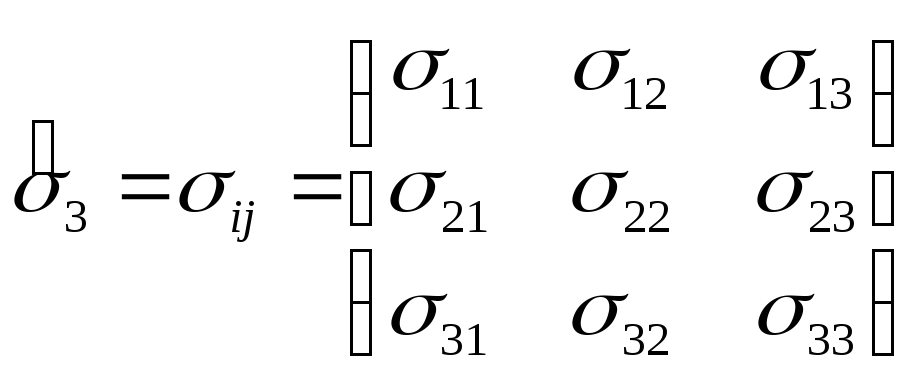(1.2)

В идеальных жидкостях и газах сдвиговая упругость отсутствует, в связи с чем касательные напряжения не возни­кают, вектора напряжений направлены навстречу действую­щей на рассматриваемый объем силе, т. е. численно равны давлению Р с обратным знаком.

Условно считая давление тензором, запишем

, (1.3)

где — тензор упругих напряжений в жидкости.

В процессе сейсмоакустических исследований среда под­вергается воздействию внешних сил, приводящему к смеще­нию ее частиц . Возникающую при этом дефор­мацию полностью определяет тензор

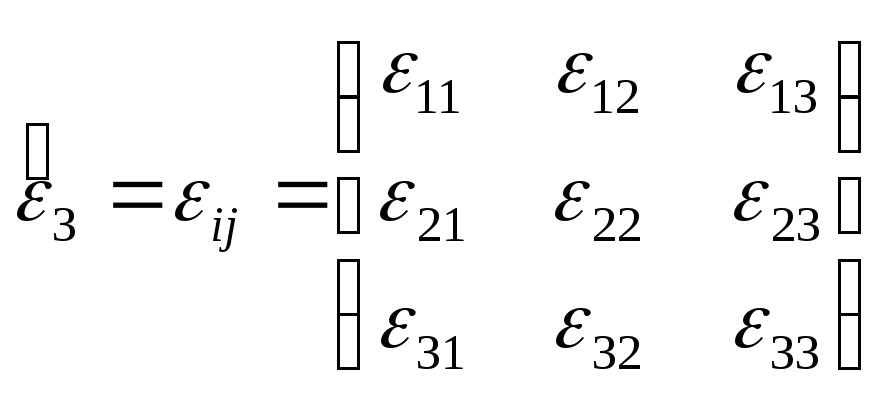(1.4а)

где при i = j — относительные удлинения (сжатия) бесконечно малых отрезков, которые до деформации были парал­лельны координатным осям; при i ≠ j — сдвиговые деформации, характеризующие изменение углов между осями координат в результате деформации. В общем случае

(1.4б)

Согласно (1.4б) сумма диагональных членов матрицы (1.4а)

,

где , — невозмущенный объем рассматриваемого элемента среды; —изменение объема. Величину называют дилатацией.

В цилиндрической системе координат удлинения (сжатия) обозначают , , , а сдвиговые деформации — , , . Их можно выразить через смещения:

; ; ;

; ; (1.5)

Линейную связь между тензором напряжения и тензором деформации при температуре T=const выражает обобщен­ный закон Гука. Для изотропной среды он имеет вид

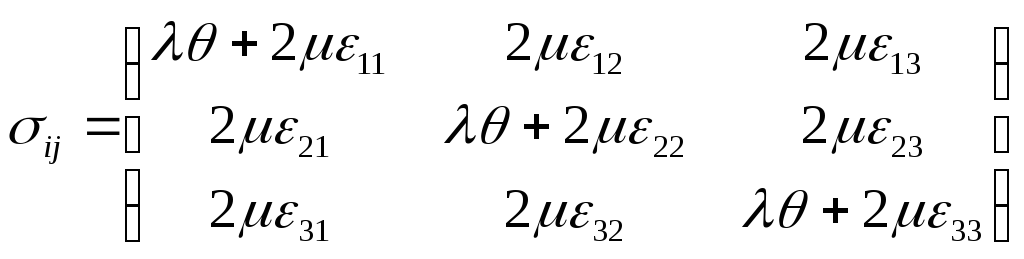(1.6)

где λ и µ — положительные величины, называемые констан­тами Ламэ.

Часто µ называют модулем сдвига, так как он определяет величину сдвига при данном касательном напряжении. Закон Гука для жидкостей и газа (µ=0) с учетом выражения (1.3) запишем в виде

, (1.7)

где —модуль всестороннего сжатия, играющий для жидко­сти роль константы Ламэ λ. Знак минус указывает на умень­шение объема с ростом давления. При характерных для сейсмоакустики слабых возмущениях

, (1.8)

где — невозмущенная плотность среды; — изменение плот­ности. Поэтому выражение (1.7) можно записать следую­щим образом:

, (1.9)

где β — адиабатическая сжимаемость жидкости.