5.8. Абсолютная и условная сходимость числовых рядов

Знакопеременный ряд называют абсолютно сходящимся, если ряд, составленный из модулей его членов, сходится. Знакопеременный ряд называют условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится.

Среди знакопеременных рядов абсолютно сходящиеся ряды занимают особое место: на такие ряды переносятся основные свойства конечных сумм (переместительность, сочетательность, распределительность).

Т.е. абсолютно сходящиеся ряды суммируются, вычитаются как обычные ряды. Суммы таких рядов не зависят от порядка записи членов. В случае условно сходящихся рядов, такие свойства, вообще говоря, не имеют места.

Степенные ряды

1 Функциональные ряды

1.1 Основные понятия

Ряд, членами которого являются функции от , называется функциональным. . Придавая определенное значение х₀ мы получаем числовой ряд , который может быть как сходящимся, так и расходящимся.

Если полученный числовой ряд сходится, то точка называется точкой сходимости ряда, если ряд расходится – точкой расходимости. Совокупность числовых значений аргумента , при которых функциональный ряд сходится, называется его областью сходимости. В области сходимости функционального ряда его сумма является некоторой суммой от : . Определяется она в области сходимости ряда равенством , где - частичная сумма ряда. Среди функциональных рядов в математике и ее приложениях особая роль принадлежит рядам, членами которых являются степенные функции аргумента , т.е. так называемые степенные ряды.

Действительные или комплексные числа , , …, … называются коэффициентами ряда, а - действительной переменной. Ряд расположен по степеням . Рассматривают такие степенные ряды, расположенные по степеням , т.е. ряд вида , где - некоторое постоянное число. Этот ряд легко приводится к первому, если положить .

1.2. Сходимость степенных рядов

Область сходимости степенного ряда содержит, по крайней мере, одну точку: , в которой ряд сходится.

Теорема Абеля. Если степенной ряд сходится при , то он абсолютно сходится при всех значениях , удовлетворяющих неравенству .

Доказательство. По условию ряд сходится. Следовательно, по необходимому признаку сходимости . Отсюда следует, что величина ограничена, т.е. найдется такое число , что для всех выполняется неравенство , . Пусть , тогда величина и следовательно, , , т.е. модуль каждого члена ряда не превосходит соответствующего члена сходящегося ряда геометрической прогрессии. Поэтому по признаку сравнения при степенной ряд абсолютно сходящийся.

Следствие. Если ряд (степенной) расходится при , то он расходится и при всех , удовлетворяющих неравенству .

1.3. Интервал и радиус сходимости степенного ряда

Из теоремы Абеля следует, что, если есть точка сходимости степенного ряда, то интервал весь состоит из точек сходимости данного ряда. При всех значениях вне этого интервала ряд расходится.

Интервал называют интервалом сходимости степенного ряда. Положив , интервал сходимости можно записать в виде . Число называется радиусом сходимости степенного ряда, т.е. - это такое число, что при всех , для которых , ряд абсолютно сходится, а при ряд расходится. В частности, когда степенной ряд сходится лишь в одной точке , то считаем, что . Если же степенной ряд сходится при всех значениях , то .

Отметим, что на концах интервала сходимости (при и =-R) сходимость ряда проверяется отдельно.

Для нахождения радиуса сходимости степенного ряда можно поступить следующим образом. Составим ряд из модулей членов данного степенного ряда и применим к нему признак Даламбера. Допустим, что существует предел , . По признаку Даламбера ряд сходится, если , т.е. ряд сходится при тех значениях , для которых . Ряд, составленный из модулей членов степенного ряда, расходятся при тех значениях , для которых . Таким образом, для степенного ряда радиус абсолютной сходимости (1).

Аналогично, воспользовавшись радикальными признаками, можно установить, что (2).

Дополнение:

1. Если , то можно убедиться, что ряд степенной абсолютно сходится на всей числовой оси. В этом случае . Если , то .

2. Интервал сходимости степенного ряда по степеням находят из неравенства и имеет вид .

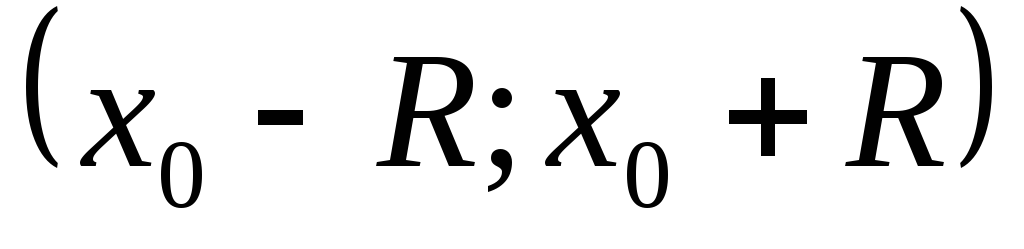3. Если степенной ряд содержит не все степени , т.е. задан неполный степенной ряд, то интервал сходимости ряда находят без определения радиуса сходимости в соответствии с формулами (1) и (2), а непосредственно применяя признак Даламбера (или Коши) для ряда, составленного из модулей членов данного ряда.

Пример 1. Найти область сходимости ряда . Воспользуемся формулой (1) , следовательно данный ряд абсолютно сходится на всей числовой оси.

Пример 2. Найти область сходимости ряда . Данный ряд неполный. Воспользуемся признаком Даламбера. Для данного ряда имеем , ; . Ряд абсолютно сходится, если или . Исследуем поведение ряда на концах интервала сходимости. При имеем ряд , который сходится по признаку Лейбница. При имеем ряд , это тоже сходящийся лейбницевский ряд. Следовательно, областью сходимости исходного ряда является отрезок .

1.4. Свойства степенных рядов

1) Сумма степенного ряда является непрерывной функцией в интервале сходимости .

2) Степенные ряды и , имеющие радиусы сходимости соответственно R₁ и R_2, можно почленно складывать, вычитать и умножать. Радиус сходимости произведения, суммы и разности этих рядов не меньше, чем меньшее из чисел R₁ и R_2,.

3) Степенной ряд внутри интервала сходимости можно почленно дифференцировать, при этом для ряда при выполняется равенство (1)

4) Степенной ряд можно почленно интегрировать на каждом отрезке, расположенном внутри интервала сходимости; при этом для степенного ряда при выполняется равенство (2). Ряды (1) и (2) имеют тот же радиус сходимости, что и исходный степенной ряд. Свойства степенных рядов широко используются в теоретических исследованиях и приближенных расчетах.