
- •Часть I Введение
- •I. Матрицы.
- •1. Основные понятия.
- •2. Действия над матрицами
- •2. Определители
- •1. Основные понятия
- •2. Свойства определителей (необходимы для вычисления определителей):
- •3. Невырожденные матрицы
- •2. Ранг матрицы
- •II. Система линейных уравнений.
- •1. Основные понятия
- •2. Решение системы линейных уравнений
- •3. Решение не вырожденных линейных систем.
- •4. Метод Гаусса
- •5. Система однородных линейных уравнений
- •6.Модель Леонтьева многоотраслевой экономики
- •III. Элементы векторной алгебры
- •1. Основные понятия
- •2. Операции над векторами
- •3. Векторное пространство и п – мерный вектор
- •3.1. Линейная зависимость векторов
- •Размерность и базис линейного пространства.
- •3.3. Разложение вектора в ортогональном базисе.
- •3.4.Переход к новому базису.
- •3.5. Линейные операторы.
- •3.6. Собственные векторы и собственные значения линейного оператора.
- •2. Симметричный оператор.
- •3. Ортогональность собственных векторов.
- •3.7.Квадратичные формы.
- •IV Аналитическая геометрия на плоскости.
- •1.Система координат. Основные понятия.
- •Линия на плоскости(основные понятия)
- •2. Уравнение прямой на плоскости
- •1) Уравнение прямой с угловым коэффициентом
- •2) Общее уравнение прямой X
- •7) Нормальное уравнение прямой
- •8) Угол между двумя прямыми
- •9) Точка пересечения прямых
- •10) Расстояние от точки до прямой
- •3.Линии второго порядка на плоскости.
- •1) Окружность
- •2) Эллипс
- •3) Гипербола.
- •Исследование формы гиперболы по ее уравнению
- •Асимптоты гиперболы
- •4) Парабола
- •Исследование формы параболы по ее уравнению
- •5) Общее уравнение линий второго порядка
- •V Аналитическая геометрия в пространстве
- •1. Уравнение поверхности и линии в пространстве
- •2.Поверхности второго порядка
- •VI. Основы математического анализа
- •1. Множества. Действительные числа
- •6. Предел функции
- •1) Предел функции в точке
- •2) Предел функции при X→∞.
- •3) Бесконечно большая функция (б.Б.Ф.).
- •4) Бесконечно малые функции.
- •6) Признаки существования пределов.
- •7) Первый замечательный предел.
- •8. Комплексные числа
- •Часть II Функции нескольких переменных
- •Функция двух переменных
- •Предел функции
- •Непрерывность функции двух переменных
- •Производные и дифференциалы функции нескольких переменных
- •Частные производные высших порядков
- •Дифференцируемость и полный дифференциал функции
- •Дифференциалы высших порядков
- •Производная сложной функции. Полная производная
- •8.Инвариантность формы полного дифференциала
- •Дифференцирование неявной функции
- •Производная по направлению
- •Градиент
- •Экстремум функции двух переменных
- •Необходимые и достаточные условия экстремума
- •II. Неопределенный интеграл
- •Понятие неопределенного интеграла
- •2. Свойства неопределенного интеграла
- •3. Таблица основных неопределенных интегралов
- •4. Основные методы интегрирования
- •5. Интегрирование рациональных функций.
- •6. Интегрирование тригонометрических функций
- •7. Интегрирование иррациональных функций
- •III. Определенный интеграл
- •Определение определенного интеграла
- •Геометрический смысл определенного интеграла
- •3) Работа переменной силы
- •Формулы Ньютона-Лейбница
- •Основные свойства определенного интеграла
- •Вычисление определенного интеграла
- •Несобственные интегралы
- •7. Применение определенных интегралов для расчета геометрических и физических величин различного рода
- •7.1. Вычисление площадей плоских фигур
- •7.2 Вычисление длины дуги плоской кривой
- •7.3 Вычисление объема тела
- •8. Приближенное вычисление определенного интеграла
- •8.1. Формулы прямоугольников
- •8.2. Формула трапеций
- •8.3. Формула парабол (Симпсона)
- •4. Кратные интегралы
- •4.1. Двойной интеграл. Основные понятия
- •4.2. Геометрический смысл двойного интеграла
- •4.3. Основные свойства двойного интеграла
- •4.4.Вычисление двойного интеграла
- •4.5. Приложения двойного интеграла
- •Статические моменты и центр тяжести плоской фигуры
- •4.6. Тройной интеграл. Основные понятия
- •4.7. Вычисление тройного интеграла.
- •4.8. Приложения тройного интеграла
- •V. Числовые ряды
- •5.1. Основные понятия
- •5.2. Необходимый признак сходимости числового ряда
- •5.3. Достаточные признаки сходимости знакопостоянных рядов
- •5.4. Признак Даламбера
- •5.5. Радикальный признак Коши
- •5.6. Интегральный признак Коши. Обобщенный гармонический ряд
- •5.7. Знакочередующиеся и знакопеременные ряды Признак Лейбница
- •5.8. Абсолютная и условная сходимость числовых рядов
- •Степенные ряды
- •1 Функциональные ряды
- •1.1 Основные понятия
- •2. Некоторые приложения степенных рядов
- •2.1. Приближенное вычисление значений функций
- •2.2. Приближенное вычисление определенных интегралов
- •VII Ряды Фурье
- •7.1. Основные понятия
- •7.2. Тригонометрический ряд Фурье
- •7.3 Разложение в ряд Фурье 2π-периодических функций. Теорема Дирихле
- •7.4. Разложение в ряд Фурье четных и нечетных функций
- •7.5. Разложение в ряд Фурье функций произвольного периода
- •VIII. Дифференциальные уравнения (д.У.)
- •8.1. Общие сведения на основании понятия о д.У.
- •8.2. Дифференциальное уравнение первого порядка
- •8.3.Дифференциальные уравнения высших порядков
- •1.Решение путем понижения порядка уравнения.
- •2.Линейные дифференциальные уравнения высших порядков.
- •8.4. Решение ду второго порядка с постоянными коэффициентами.
- •1.Решение лоду второго порядка с постоянными коэффициентами.
- •2. Решение лоду n –го порядка с постоянными коэффициентами.
- •Линейные неоднородные дифференциальные уравнения (лнду)
- •1.Структура общего решения лнду второго порядка.
- •2.Метод вариации произвольных постоянных.
- •3.Решение лнду второго порядка с постоянными коэффициентами и правой частью специального вида.
- •4.Решение лнду n- го порядка с постоянными коэффициентами и правой специальной частью.
- •Системы дифференциальных уравнений
- •Решение нормальных систем.
- •2.Системы линейных ду с постоянными коэффициентами.
6. Интегрирование тригонометрических функций
Рассмотрим несколько вариантов нахождения
интегралов от тригонометрических
функций. Для простоты обозначим
![]() - функцию с переменными
- функцию с переменными
![]() ,
над которыми выполняются рациональные
действия (сложение, вычитание, умножение
и деление).
,
над которыми выполняются рациональные
действия (сложение, вычитание, умножение
и деление).
-
вычисление интегралов типа
 сводится к вычислению интегралов от
рациональной функции подстановкой
сводится к вычислению интегралов от
рациональной функции подстановкой
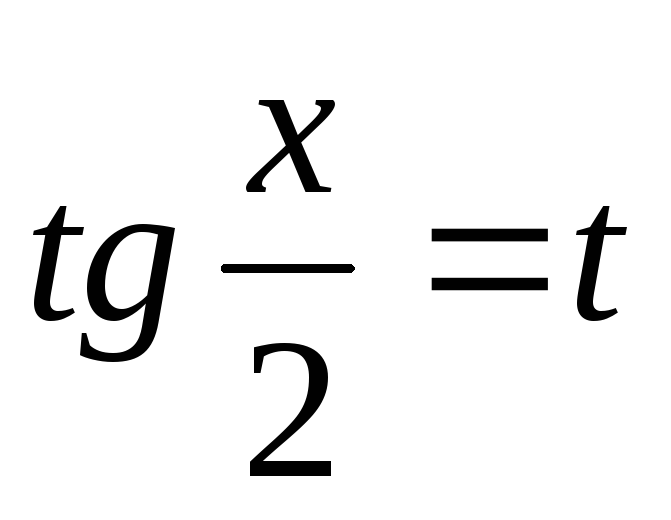 ,
которая называется универсальной.
Действительно,
,
которая называется универсальной.
Действительно,
 ;
;
 ;
;
 .
Поэтому
.
Поэтому
 =
= ,
где R1(t)
– рациональная функция от t.
Обычно этот способ довольно громоздок,
но всегда приводит к определенному
результату. На практике применяют и
другие более простые подстановки в
зависимости от свойств подынтегральной
функции.
,
где R1(t)
– рациональная функция от t.
Обычно этот способ довольно громоздок,
но всегда приводит к определенному
результату. На практике применяют и
другие более простые подстановки в
зависимости от свойств подынтегральной
функции.
а) если функция
![]() нечетна относительно sinx,
т.е.
нечетна относительно sinx,
т.е.
![]() =
=![]() ,
то можно применить подстановку cosx=t.
,
то можно применить подстановку cosx=t.
б) если
![]() нечетна относительно cosx,
т.е.
нечетна относительно cosx,
т.е.
![]() =
=![]() ,
то применяют подстановку sinx=t.
,
то применяют подстановку sinx=t.
в) если функция четная относительно
Sinx и Cosx
![]() =
=![]() ,
то можно использовать подстановку
tgx=t. Такая
же подстановка используется, если
интеграл имеет вид
,
то можно использовать подстановку
tgx=t. Такая
же подстановка используется, если
интеграл имеет вид
![]() .
.
г) интеграл типа
![]() .
.
Для нахождения таких интегралов используются следующие приемы:
-
подстановка sinx=t, если n – целое положительное нечетное число.
-
подстановка cosx=t, если m - целое положительное нечетное число.
-
формулы понижения порядка
 ,
, ,
,
![]() ,
если m,n –
целые неотрицательные четные числа.
,
если m,n –
целые неотрицательные четные числа.
-
Подстановка tgx=t, если m+n – четное отрицательное целое число.
Пример:
![]() ;
;
![]() ,
тогда
,
тогда
![]()
7. Интегрирование иррациональных функций
Рассмотрим некоторые типы интегралов, содержащих иррациональные функции.
а) интегралы типа
![]() называются неопределенными интегралами
от квадратичных иррациональностей. Их
находят следующим образом: под радикалом
выделяют полный квадрат:
называются неопределенными интегралами
от квадратичных иррациональностей. Их
находят следующим образом: под радикалом
выделяют полный квадрат:
![]() и делают подстановку.
и делают подстановку.
![]() .
При этом первые два интеграла приводятся
к табличным, а третий – к сумме двух
табличных интегралов.
.
При этом первые два интеграла приводятся
к табличным, а третий – к сумме двух
табличных интегралов.
Пример:
![]() .
Т.к.
.
Т.к.
![]() ,
то
,
то
 .
Сделав подстановку
.
Сделав подстановку
![]() ,
тогда
,
тогда
 .
.
б) Интегралы типа
![]() ,
где Pn(x)
– многочлен степени n
можно вычислить пользуясь формулой
,
где Pn(x)
– многочлен степени n
можно вычислить пользуясь формулой
![]() (1)
(1)
где Qn-1(x)
– многочлен степени (n-1)
с неопределенными коэффициентами,
![]() -
также неопределенный коэффициент. Все
неопределенные коэффициенты находятся
из тождества получаемого дифференцированием
обоих частей равенства. (1)
-
также неопределенный коэффициент. Все
неопределенные коэффициенты находятся
из тождества получаемого дифференцированием
обоих частей равенства. (1)
![]() после чего необходимо приравнять
коэффициенты при одинаковых степенях
неизвестной х.
после чего необходимо приравнять
коэффициенты при одинаковых степенях
неизвестной х.
в) Дробно-линейная подстановка
Интегралы типа
![]() ,
где
,
где
![]() ,
b, c, d
– действительные числа,
,
b, c, d
– действительные числа,
![]() - натуральные числа, сводящиеся к
интегралам от рациональной функции
путем подстановки
- натуральные числа, сводящиеся к
интегралам от рациональной функции
путем подстановки![]() k – наименьшее общее
кратное знаменателей дробей
k – наименьшее общее
кратное знаменателей дробей
![]() Действительно из подстановки
Действительно из подстановки
![]() ,
следует, что
,
следует, что
![]() и
и
![]() ,
т.е. x и dx
выражаются через рациональные функции
от t. При этом и каждая
степень дроби
,
т.е. x и dx
выражаются через рациональные функции
от t. При этом и каждая
степень дроби
![]() выражается через рациональную функцию
от t.
выражается через рациональную функцию
от t.
г) Интегралы типа
![]() .
.
Здесь подынтегральная функция –
рациональная функция относительно
![]() и
и
![]() .
Выделив под радикалом полный квадрат
и сделав подстановку
.
Выделив под радикалом полный квадрат
и сделав подстановку
![]() ,
и интегралы данного типа приводятся к
интегралам уже рассмотренного типа,
т.е. к интегралам типа
,
и интегралы данного типа приводятся к
интегралам уже рассмотренного типа,
т.е. к интегралам типа
![]() ;
;![]() ;
;![]() .
Эти интегралы вычисляются с помощью
соответствующих тригонометрических
подстановок:
.
Эти интегралы вычисляются с помощью
соответствующих тригонометрических
подстановок:
![]() - для интегралов первого типа,
- для интегралов первого типа,
![]() - второго и
- второго и
![]() для интегралов третьего типа.
для интегралов третьего типа.
Следует отметить, что операции интегрирования функции значительно сложнее операции дифференцирования функций на практике при вычислении интегралов используют различные справочники, содержащие таблицы наиболее часто встречающихся интегралов.
Однако зачастую интеграл выражается через элементарные функции, в этом случае говорят, что интеграл не теряется (или его нельзя найти).
Так, например, нельзя взять интеграл
![]() ,
так как не существует элементарной
функции, производная от которой была
бы равна
,
так как не существует элементарной
функции, производная от которой была
бы равна
![]() .
.
