2.Поверхности второго порядка

1) Цилиндрические поверхности.

Поверхность, образованная движением прямой L, которая перемещается в пространстве, сохраняя постоянное направление, и пересекает каждый раз некоторую кривую K, называется цилиндрической поверхностью или цилиндром. При этом кривая K- называется направляющей, а L – образующей цилиндра. Будем рассматривать цилиндрические поверхности, направляющие которых лежат в одной из координатных плоскостей, а бразующие || координатной оси, то есть перпендикулярно этой плоскости. Пусть в Oxy лежит линия K, а ее уравнение F(x,y)=0. Построим цилиндр с образующими || оси Oz и направляющей K.

В

. M (x,y,z)

L

N

K

x

z

y

Рис.1.

озьмем на цилиндре любую точку M(x,y,z). Она лежит на какой-то образующей. Пусть т.N- точка пересечения этой образующей с плоскостью Oxy. Следовательно, точка N лежит на кривой K, и ее координаты удовлетворяют уравнению линии K. Но точка M имеет такие же абсциссу x и ординату y , что и точка N.

Следовательно, этому уравнению удовлетворяют и координаты точки M(x,y,z), так как оно не содержит Z. Так как M- любая точка цилиндра то уравнение F(x,y)=0, и будут уравнения цилиндра с образующими || оси Oz. В случае если образующая || оси Oy F(x,y)=0, если образующая || оси Ox; F(y,z)=0.

Название цилиндра определяется формой направляющей. Если направляющей служит эллипс, в плоскости Oxy, то цилиндрическая поверхность называется эллиптическим цилиндром частный случай эллипса- окружность дает круговой цилиндр и т.д. все эти поверхности называются цилиндрами второго порядка, т.к. их уравнения есть уравнения второй степени.

2) Поверхности вращения. Конические поверхности.

Поверхность, образованная вращением некоторой плоской кривой вокруг оси, лежащей в ее плоскости называется поверхностью вращения. Пусть некоторая кривая L лежит в плоскости Oyz. Уравнения этой кривой запишут в виде :

(1)

O₁(0,0,z₁)

y

L

N (0,y₁,z₁)

M (x,y,z)

Рис.2.

Найдем уравнение поверхности образованное вращением кривой L вокруг оси Oz. Для этого возьмем на поверхности произвольную т.M(x,y,z). Проведем через M плоскость перпендикулярную оси Oz. Обозначим точки пересечения ее с осью Oz и кривой L соответственно O₁ и N. Тогда O₁(0,0,z), а N(0,,z₁). Отрезки O₁M и O₁N являются радиусами одной и той же окружности. Поэтому O₁M=O₁N, но

а тогда или , кроме того Z₁=Z .

Так как точка N лежит на кривой L , то ее координаты удовлетворяют уравнениям (1). Стало быть, F(y₁,z₁)=0,исключая вспомогательные координаты y₁ и z₁ придем к соотношению

- это искомое уравнение .

Это уравнение - поверхности вращения, ему удовлетворяют координаты любой точки M этой поверхности и не удовлетворяют координаты точек не лежащих на поверхности вращения.

Если кривая вращается вокруг других осей Ox и Oy, то уравнение будет носить аналогичный характер соответственно и . Так , например, вращая прямую y=z вокруг оси Oz получим поверхность вращения описываемую уравнением или - это конус второго порядка

Поверхность, образованная прямыми линиями, проходящими через данную точку p и пересекающими данную плоскую линию L( не проходящую через p) называются конической поверхностью или конусом. При этом L- направляющая конуса p- ее вершина, а прямая описывающая поверхность называется образующей.

Пусть направляющая L задана уравнениями:

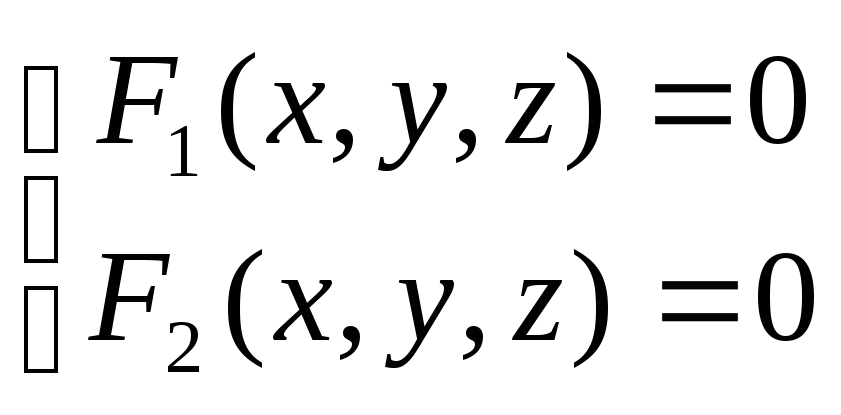
L

А точка P(x₀,y₀,z₀) -вершина конуса. Найдем уравнение конуса.

В

M(x,y,z)

N(x₁,y₁,z₁)

P(x₀,y₀,z₀)

Рис.3.

озьмем на поверхности конуса произвольную точку M(z,y,z)(рис.3). Образующая, проходящая через точки P и M, пересекает направляющую L в некоторой точке N(x₁,y₁,z₁) координаты точки N удовлетворяют выше записанным соотношениям, следовательно:

А канонические уравнения образующих проходящих через т.P и т. N имеют вид.

Исключая из этих уравнений , и получим уравнение конической поверхности связывающее текущие координаты x, y и z.

Пример : составить уравнение конуса с вершиной в т.О(0,0,0).Если направляющая - эллипс

, лежащий в плоскости Z₁=с.

Решение: Каноническое уравнение образующих, проходящих через т.О(0,0,0) и т.N(x₁,y₁,z₁), полученную при пересечении образующей OM с эллипсом, будет учитывая, что Z₁=с, получим: , откуда ; Подставляя значения x₁ и y₁ в уравнение эллипса, с учетом того, что N(x₁,y₁,z₁) лежит на эллипсе, можно получить , подставляя сюда ранее полученное значения x₁ и y₁ получим или окончательно - это и есть уравнение конуса.

3) Канонические уравнения поверхностей второго порядка.

По заданному уравнению поверхности второго порядка(те поверхности, уравнение которой в прямоугольной системе координат является алгебраическим уравнением второго порядка) будем определять ее геометрическим вид. Для этого применим так называемый метод сечений: исследование вида поверхности будем производить при помощи изучения линий пересечения данной поверхности с координатными плоскостями или плоскостями им параллельными.

а) Эллипсоид

Исследуем поверхность, заданную уравнением:

Рассмотрим сечения поверхности описываемой этим уравнением с плоскостями || плоскости Oxy. Уравнения этих плоскостей Z=h, где h- любое число. Линия, получаемая в сечении, будет определяться двумя уравнениями:

(1)

Исследуем это уравнение.

а) Если |h|>c, c>0, то . Точек пересечения нашей поверхности с плоскостями Z=h не существует;

б) Если |h|<c , то уравнения (1) можно записать в виде: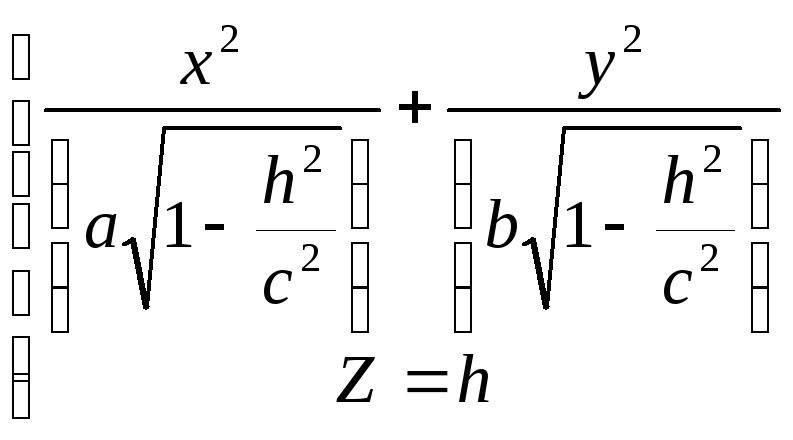=1

т.е. линия пересечения есть эллипс с полуосями:

;

При этом, чем меньше |h|, тем больше полуоси ₁ и b₁ , при h=0 они достигают своих max значений ₁=, b₁=b. Уравнение примет вид:

с

z

c

x

y

b

Рис.4.

Аналогичные результаты получим, если рассмотрим сечение поверхности плоскостями x=h и y=h. Таким образом, рассмотренные сечения позволяют изобразить рассмотренную поверхность как замкнутую овальную поверхность, называемую эллипсоидом(Рис.4.). Величины ,b,c- называются полуосями

эллипсоида, если ≠ b≠ c, то эллипсоид называется трехосным. Если какие-либо две равны, то получается эллипсоид вращения. Если =b=c, то получим сферу - .

б) Однополостный гиперболоид.

Исследуем поверхность, заданную уравнением:

=1

Пересекая эту поверхность плоскостью Z=h, получим линию пересечения, уравнение которой имеет вид:

или

Как видно, этой линий является эллипс с полуосями:

и

П

h

олуоси ₁ и b₁ достигают min при h=0, ₁= и b₁=b. При возрастании |h| ₁ и b₁ будут возрастать.

Е

a₁

a

b₁

b

y

сли пересекать эту поверхность плоскостями x=h и y=h, то в сечении получим гиперболы. Найдем, например, линию пересечения нашей поверхности с полуосью Oyz, уравнение которой x=0. Подставляя, получим:

x

Рис.5.

-это гипербола

Анализ сечений показывает, что поверхность, определяемая нашим уравнением, имеют форму бесконечно расширяемой трубки. Эта поверхность называется однополостным гиперболоидом (рис.5.).

с) Двухполосной гиперболоид

Пусть поверхность задана уравнением:

Если эту поверхность пересечь плоскостью Z=h, получим линию пересечения, описываемую уравнениями:

Отсюда следует, что :

а) если |h|<c, то Z=h не пересекает поверхность;

б) если |h|=с, то плоскости Z=c касаются данной поверхности в точках (0,0,c) и (0,0,-c);

в) если |h|>c, то уравнения можно записать так:

- эти уравнения определяют эллипс, полуоси которого возрастают с ростом |h|.

П

z

ересекая поверхность координатными плоскостями Oyz(x=0) и Oxz(y=0), получим в сечении гиперболы, уравнения которых соответственно:

У

x

y

h

Рис.6.

обеих гипербол действительной осью является ось Oz. Метод сечений позволяет изобразить эту поверхность, как поверхность, состоящую из двух полостей, имеющих форму выпуклых неограниченных чаш. Эта поверхность называется двуполостным гиперболоидом (рис.6.).

д) Эллиптический параболоид

Исследуем поверхность, заданную уравнением

где p>0, >0. Рассечем эту поверхность плоскостью Z=h. в сечении получим линию, уравнение которой есть

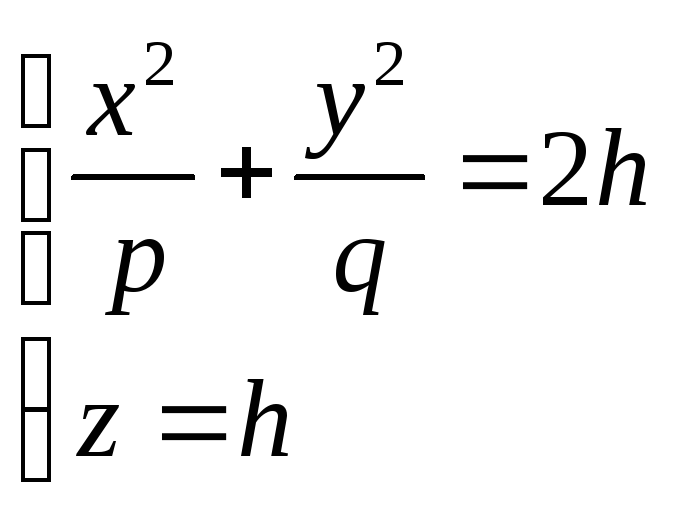
а

z

) если h<0, плоскости Z=h поверхность не пересекает;

б) если h=0, то Z=0 касается поверхности в т.O(0,0,0);

в

h

) если h>0,то в сечении- эллипс уравнение которого имеет вид:

x

y

Рис.7.

его полуоси возрастают с ростом h.

При пересечении Oxz и Oyz получатся параболы:

и

Таким образом, поверхность будет иметь вид выпуклой бесконечно расширяющейся чаши- это эллиптический параболоид (рис.7.).

е) Гиперболический параболоид

Исследуем поверхность, определяемую уравнением:

где p>0, q>0. Рассечем эту поверхность плоскостями Z=h. Получим кривую, которая при h≠0 является гиперболой:

1) при h>0 ее действительные оси параллельны оси Ox;

2) при h<0 параллельны оси OY:

3) при h=0 линия пересечения распадается на пару пересекающихся прямых: и .При пересечении поверхности плоскостями || плоскости Oxy, будут получаться параболы:

ветви которых направлены вверх. П

z

0

y

ри y=0 в сечении получим параболу с вершиной в т.О(0,0,0) и осью симметрии Oz.

x

П

Рис.8.

ересекая нашу поверхность плоскостями x=h, получим параболы :

ветви которых направлены вниз.

Анализ линий пересечения позволяет определить, что она имеет вид седла (рис.8.). Эта поверхность- гиперболический параболоид.