4) Парабола

Параболой называется множество всех точек плоскости, каждая из которых одинаково удалены от данной точки, называемой фокусом и данной прямой называемой директрисой. Расстояние от фокуса до директрисы называется параметром параболы и обозначается p(p>0). Для вывода уравнения параболы выберем системы координат Oxy так, чтобы ось Ox проходила через F перпендикулярно директрисе в направлении от директрисы к F а начало координат О расположим посредине между фокусом и директрисой(рис.6). В выбранной системе F имеет координаты , а уравнение директрисы имеет вид или .

П

y

M (x, y)

N

усть M(x,y) - произвольная точка параболы. Соединим т.M с F. Проведем отрезок MN перпендикулярный директрисе. Согласно определению параболы MF=MN. По формуле расстояния между точками находим а

С

0

F

N

Рис.6.

ледовательно

Возводя в квадрат

Отсюда - каноническое уравнение параболы.

Исследование формы параболы по ее уравнению

1. В уравнении y- в четной степени, значит, парабола симметрична относительно оси Ox. Ось Ox- ось симметрии параболы.

2. Т

   

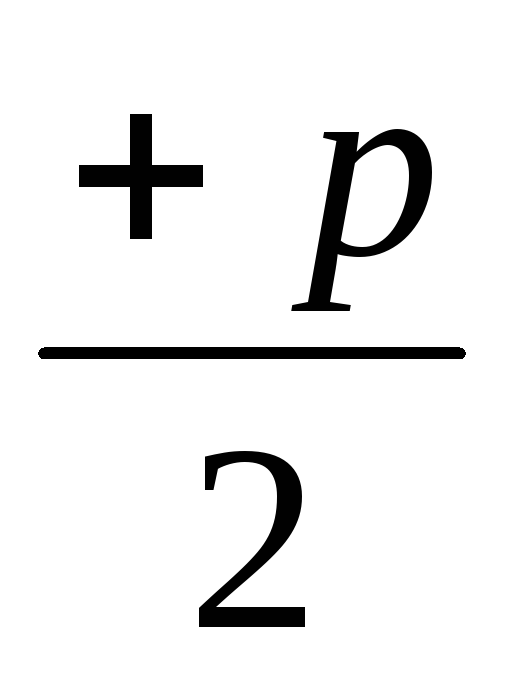
   M

   

   ак как P>0, то следует, что x≥0 следовательно парабола расположена справа от оси Ox.

3. П

   r

   F

   0

   ри x=0 имеем y=0. следовательно, парабола проходит через начало координат.

4. П

   Рис.7.

   ри неограниченном возрастании x модуль y также неограниченно возрастает. Парабола y²=2px имеет вид, изображенный на рис.7. Тогда O(0,0) называется вершиной параболы, а отрезок FM=r –фокальный радиус точки M.

5) Общее уравнение линий второго порядка

Запишем уравнение эллипса, окружности, гиперболы и параболы с центрами в т.O₁(x₀,y₀), оси симметрии которых параллельны координатным осям Ox и Oy. Для этого надо поместить в т.O₁(x₀,y₀), начало новой системы координат O₁(x'₁,y'₁), оси которой O₁x' и O₁y' параллельны соответствующим осям Ox и Oy, и одинаково с ними направлены. Так как и -формулы параллельного переноса, то в старой системе координат после подстановки значений x’ и y’ в формулы соответствующих кривых получим:

(уравнение эллипса),

-уравнение гиперболы.

-уравнение окружности

-уравнение параболы.

Можно легко показать после несложных преобразований, что все эти уравнения можно записать с помощью единого уравнения следующего вида:

Где A,C≠ 0 одновременно.

Возникает вопрос :всякое ли уравнение приведенного вида определяет одну из кривых (окружность, эллипс, гипербола, парабола). Ответ дает теорема.

Теорема. Приведенное уравнение всегда определяет: либо окружность(при A=C),либо эллипс(при >0), либо гиперболу (при <0), либо параболу (при =0). При этом возможны случаи вырождения: для эллипса (окружность) - в точку или мнимый эллипс(окружность), для гиперболы- в пару пересекающихся прямых, для параболы- в пару параллельных прямых.