Представление отрицательных чисел в сок

Рассмотрим правила выполнения операций вычитания в системе остаточных классов для чисел А и В, удовлетворяющих условию А-В [0,].

А = (₁, ₂, ... ,_n),

В = (₁, ₂, ... ,_n),

A-B = (₁, ₂, ... ,_n),

при этом А<ρ, B< ρ, 0<=А-В< ρ.

Как и ранее, получаем для А-В:

_i = _i - _i - ,

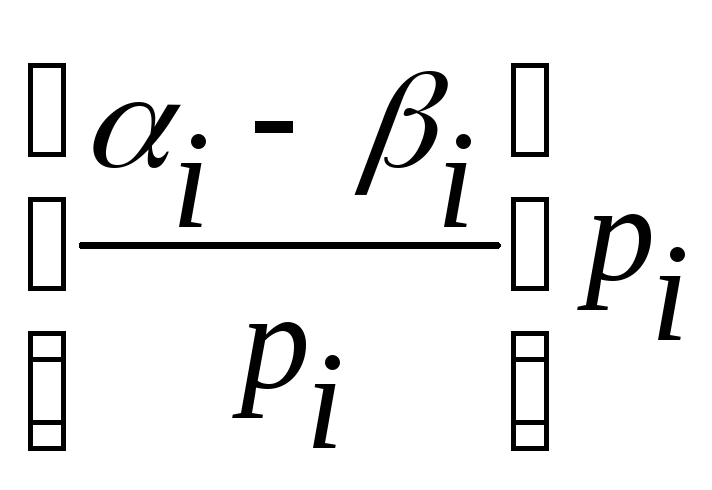_i  _i - _i (mod p_i).

Операция вычитания при положительном результате выполняется вычитанием соответствующих цифр разрядов, в результате приводится наименьший положительный остаток.

При отрицательной разности цифр берется ее дополнение к основанию. При этом знак результата в результате никак не отражен.

Возникает необходимость ввести специальным образом знак в представление числа и определить правила выполнения операций, обеспечивающих получение не только величин, но и знака результата.

Рассмотрим варианты введения отрицательных чисел.

Пусть p₁, p₂, ... p_n - основания системы счисления.

= p₁, p₂, ... ,p_n - диапазон представимых чисел.

Пусть p₂ =2. Обозначим через В СОK Р=(1, 0, 0, ... , 0). Будем оперировать числами, лежащими в диапазоне 0≤ |N| <P.

Примем в качестве нуля число Р и представим положительные числа N= =|N| как N' = P + |N|, отрицательные числа N = - |N| как N' =P - |N|. Таким образом, N' =P+N - искусственная форма (общая форма представления + и - чисел).

Следовательно, мы всегда будем иметь дело с положительными числами, так как |N|<P.

Но числа в интервале [0,P) в искусственной форме будут отображать отрицательные, а в интервале [P,) - положительные числа.

Операцию сложения и вычитания можно выполнять следующим образом:

N′₁ = P + N₁,

N′₂ = P + N₂,

N′₁ + N′₂ = P + N₁ + P + N₂ = 2P + (N₁ + N₂).

Для суммы N₁ + N₂ искусственная форма:

(N₁ + N₂)′ = P + (N₁ + N₂),

(N′₁ + N′₂) = N′₁ + N′₂ - P

или, так как P = (1, 0, 0, ..., 0), то (N₁ + N₂) ′ =N′₁ + N′₂ + P. (9)

Пример. Пусть p₁ = 2, p₂ = 3, p₃ = 5, p₄ = 7.

P = 3∙5∙7 = 105,

N₁ = 17, N₂ = 41,

N′₁ = (1, 0, 0, 0) + (1, 2, 2, 3) = (0, 2, 2, 3),

N′₂ = (1, 0, 0, 0) + (1, 2, 1, 6) = (0, 2, 1, 6).

Согласно (9) (N₁ + N₂) ′ = (0, 2, 2, 3) + (0, 2, 1, 6) + (1, 0, 0, 0) = (1, 1, 3, 2) - искусственная форма N₁ + N₂, что можно проверить, перейдя к десятичной системе счисления.

(17 + 41)′ = (58)′ = 105 + 58 = (1, 0, 0, 0) + (0, 1, 3, 2) = (1, 1, 3, 2).

Пример. N₁ = 17, N₂ = 41.

N′₁ = (0, 2, 2, 3),

N′₂ = (1, 0, 0, 0) - (1, 2, 1, 6) = (0, 1, 5, 1),

(N₁ + N₂)′ = (0, 2, 2, 3) + (0, 1, 5, 1) + (1, 0, 0, 0) = (1, 0, 1, 4),

(17 - 41)′ = (-24)′ = 105 - 24 = (1, 0, 0, 0) - (0, 0, 4, 3) = (1, 0, 1, 4).

Переход из положительного числа в отрицательное и обратно, то есть образование его дополнительного кода, производится вычитанием данного числа из числа (1, p₁, p₂, ... ,p_n).

+41 = (1, 2, 1, 6),

- 41 = (1, 3, 5, 7) - (1, 2, 1, 6) = (0, 1, 4, 1) = 64.

Следует отметить, что если вычитаемое уже было представлено в искусственной форме, то для получения дополнительного кода надо его вычитать из (2,p₁,p₂, ..., p_n).

Контроль работы цифрового автомата

В процессе вычислений происходит постоянная передача и преобразование информации, находящейся в памяти ЭВМ, арифметическом или управляющем устройствах. Таким образом, при проектировании ЭВМ необходимо предусмотреть меры как выявления ошибок, так и их исправления. Эта функция возлагается на систему контроля. Система контроля – совокупность аппаратных и программных методов и средств, обеспечивающих определение правильности работы автомата в целом или его отдельных узлов, а также автоматическое исправление выявленных ошибок. Различают следующие виды ошибок вычислений, возникающих:

• из-за погрешностей в исходных данных;

• вследствие методических погрешностей;

• из-за неисправностей в работе машины.

Третий вид ошибок является объектом для системы контроля. Решение задачи контроля возможно только при наличии определенной избыточности информации (аппаратной или информационной). Аппаратная избыточность может заключаться, например, в дублировании арифметических устройств. Логические методы могут заключаться в выполнении ”двойного счета” и последующего сравнения результатов, в проверке соотношений вычисляемых функций (sin²x+cos²x=1), в контроле результата при изменении шага вычисления и так далее. Однако эти методы направлены на выявление факта появления ошибки в вычислении, но не определяют место, где она произошла.