1.1 Визначення внутрішніх нормальних сил в стержнях системи.

Звільняємо шарнір А від зв’язків (стержнів), замінюючи їх дію реакціями N₁ та N₂. Будуємо розрахункову схему задачі (рис. 1.1), обираємо осі координат та складаємо рівняння рівноваги:

Σ F_кx= 0: F₂cos 60º+ F₁cos 30º − N₂cos 20º = 0; (1.1)

Σ F_кy= 0: N₁ + F₂cos 30º− F₁cos 60º − N₂cos 70º = 0, (1.2)

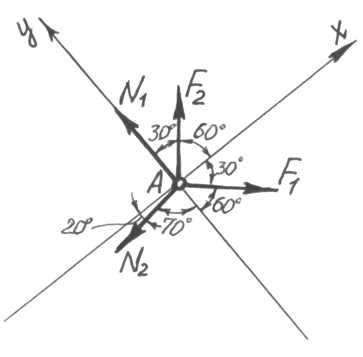
Рис. 1.1

Із рівняння (1.1) визначаємо N₂:

N₂ = 76,58 кН

Із рівняння (1.2) визначаємо N₁:

N₁ = − F₂cos 30º+ F₁cos 60º + N₂cos 70º =

= − 40 cos 30º+ 60 cos 60º + 76,58 cos 70º = 21,55 кН

N₁ = 21,55 кН

N₂ = 76,58 кН

1.2 Перевірка міцності стержнів.

Перевірку міцності стержнів виконуємо за умовою міцності при розтязі-стисканні:

, (1.3)

де σ – нормальна напругв в перерізі стержня, Н/мм²;

N – нормальна сила в перерізі, Н;

A – площа поперечного перерізу, мм²;

[σ] – допустима напруга, Н/мм².

1. Визначаємо напруги в поперечних перерізах стержнів

За формулою (1.5):

Стержень 1 недовантажений (σ₁ < [σ]);

Стержень 2 перевантажений (σ₂ > [σ]).

2. Обчислюємо відсоток недовантаження першого стержня та перевантаження другого стержня.

Δ₁ = % = % = 71,7 %

Δ₂ = % = % = 0,7 %

Недовантаження першого стержня перевищує допустимі 10 %, тобто він є неекономічним і для нього слід підібрати інший переріз.

Перевантаження другого стержня знаходиться в межах допустимих 5 %, тобто його змінювати не треба.

1.3 Підбір перерізу першого стержня.

Для першого стержня обираємо круглий переріз та визначаємо його діаметр.

1. За умовою міцності (1.5) виконуємо проектний розрахунок стержня

Для круглого перерізу , звідки визначаємо потрібний діаметр стержня:

d₁ =

Округляємо діаметр до стандартного значення:

d_1ст =15 мм

1.3.2 Для прийнятого профілю з d_1ст =15 мм визначимо відсоток перевантаження:

Δ_1ст = % = % =1,7 % < 5 %.

Відповідь: перевірка міцності стержнів показала, що для першого стержня доцільно змінити профіль перерізу на круглий з діаметром d_1ст =15 мм, а для другого стержня переріз можна залишити незмінним – здвоєні нерівнобічні кутники 50×32×4.

2 Визначення головних центральних моментів інерції складного перерізу

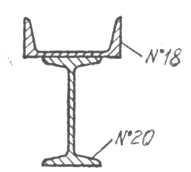
Для заданого складного перерізу визначити положення головних центральних осей та обчислити головні центральні моменти інерції.

Розв’язок

2.1. Визначення координат центру ваги перерізу.

2.1.1 Розбиваємо переріз на окремі прості частини та визначаємо їх площі:

Ι – двотавр № 20

ІІ – швелер № 18

За даними таблиць сортаментів [3]:

А₁ = 26,8 см²

А₂ = 20,7 см²

2.1.2 Обираємо довільні осі координат x та y: вісь x проводимо по нижньому основанню двотавра, а вісь y суміщаємо з віссю симетрії перерізу (див. рис. 2.1)

2.1.3 Визначаємо координати центрів ваги окремих частин, користуючись даними таблиць сортаментів [3]:

x_c1= 0

x_c2= 0

y_c1= h₁ = ∙ 20 = 10 см

y_c2= h₁+ z₀₂ = 20 + 1,94 = 21,94 см

2.1.4 Координати центру ваги складного перерізу визначаються за формулами:

x_c = ; (2.1)

y_c = , (2.2)

де А₁ , А₂ ,…, А_n – площі перерізів простих частин, см²;

x_c1 , x_c2 ,…, x_{c n} - координати центрів ваги простих частин по осі x, см;

y_c1 , y_c2 ,… , y_{c n} - координати центрів ваги простих частин по осі y, см.

Для заданого перерізу, який складається з 2-х простих частин:

x_c == 0 см

y_c = см