2 Геометричні характеристики плоских перерізів

2.1 Теоретичні положення.

Міцність та жорсткість конструкцій при крученні, згині, складному навантаженні залежить не тільки від матеріалу і діючих навантажень, але і від форми перерізу та від його орієнтації відносно прикладених навантажень. Для того, щоб раціонально навантажувати конструкцію, необхідно знати геометричні характеристики її перерізу, а також положення головних центральних осей інерції, відносно яких моменти інерції мають екстремальні значення. Основними геометричними характеристиками перерізу є його площа, статичні моменти інерції, осьові, полярний та відцентровий моменти інерції.

1. Площа перерізу А, см² або м²;

2. Статичний момент перерізу відносно осей x та y: S_x , S_y , см³ або м³.За відомими статичними моментами можна визначити координати центру ваги перерізу: x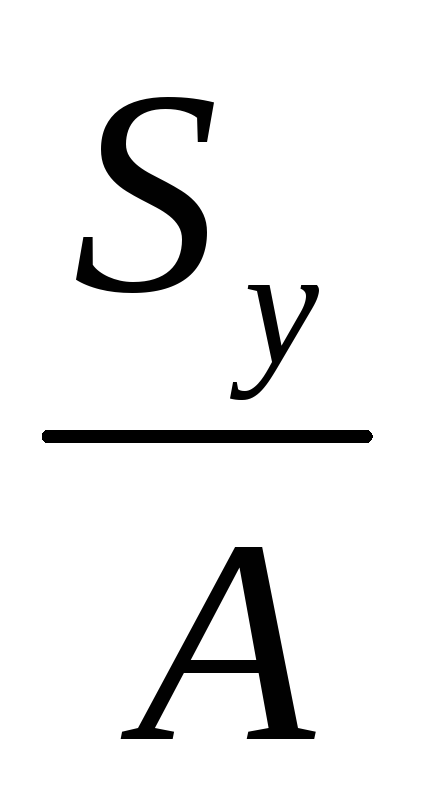_c = ; y_c = 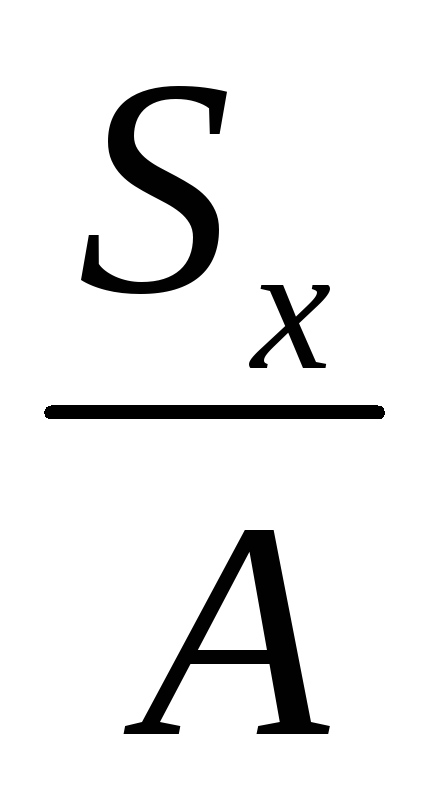. Якщо переріз складається з декількох простих фігур, то координати його центру ваги визначаються наступним чином:

x_c = ; (2.1)

y_c = , (2.2)

де А₁ , А₂ ,…, А_n – площі перерізів простих частин, см²;

x_c1 , x_c2 ,…, x_{c n} - координати центрів ваги простих частин по осі x, см;

y_c1 , y_c2 ,… , y_{c n} - координати центрів ваги простих частин по осі y, см.

3. Осьові моменти інерції перерізу відносно осей x та y: I_x , I_y ,см⁴ або м⁴;

4. Полярний момент інерції перерізу I_p , см⁴ або м⁴;

5. Відцентровий момент інерції перерізу I_xy , см⁴ або м⁴.

Головні центральні осі перерізу – це осі, які проходять через центр ваги перерізу і відносно яких осьові моменти інерції набувають екстремальних значень. Якщо переріз має хоча б одну вісь симетрії, то одна з головних центральних осей співпадає з нею. Друга головна центральна вісь проходе через центр ваги перпендикулярно до першої.

Між моментами інерції відносно центральних осей (I_X і I_Y ) та відносно осей, що паралельні центральним (I_x і I_y ), існує зв'язок:

I_X = I_x + a² ∙ A; (2.3)

I_Y = I_y+ b² ∙ A, (2.4)

де а – відстань між осями X та x, см;

b - відстань між осями Y та y, см;

А – площа перерізу, см².

Моменти інерції складного перерізу дорівнюють сумі моментів інерції його складових частин:

I_X = I_X^І + I_X^ІІ + … + I_Xⁿ ; (2.5)

I_Y = I_Y^І + I_Y^ІІ + … + I_Yⁿ , (2.6)

де I_X - момент інерції всього перерізу відносно осі X, см⁴;

I_Y - момент інерції всього перерізу відносно осі Y, см⁴;

I_X^І, I_X^ІІ,…, I_Xⁿ - моменти інерції складових частин відносно осі X, см⁴;

I_Y^І, I_Y^ІІ, … , I_Yⁿ - моменти інерції складових частин відносно осі Y, см⁴.

2. Умова та вихідні дані задачі 2.

Задача 2. «Визначення головних центральних моментів інерції складного перерізу»

Для заданого складного перерізу визначити положення головних центральних осей та обчислити головні центральні моменти інерції.

Вихідні дані та вигляд перерізу – див. рис. 2.1 а, б, в.

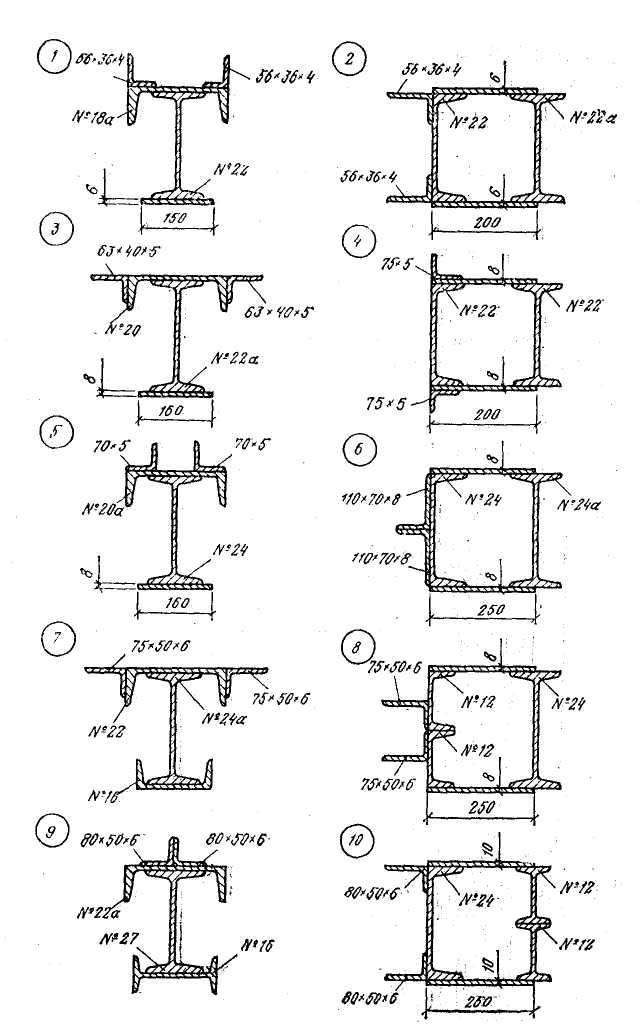
Рис 2.1 а

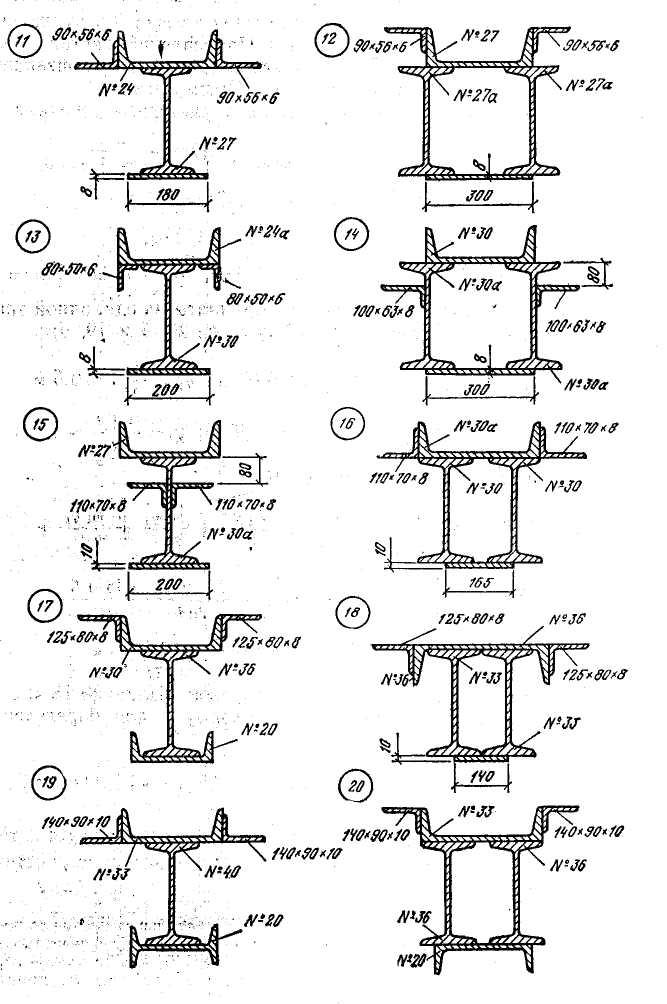
Рис. 2.1 б

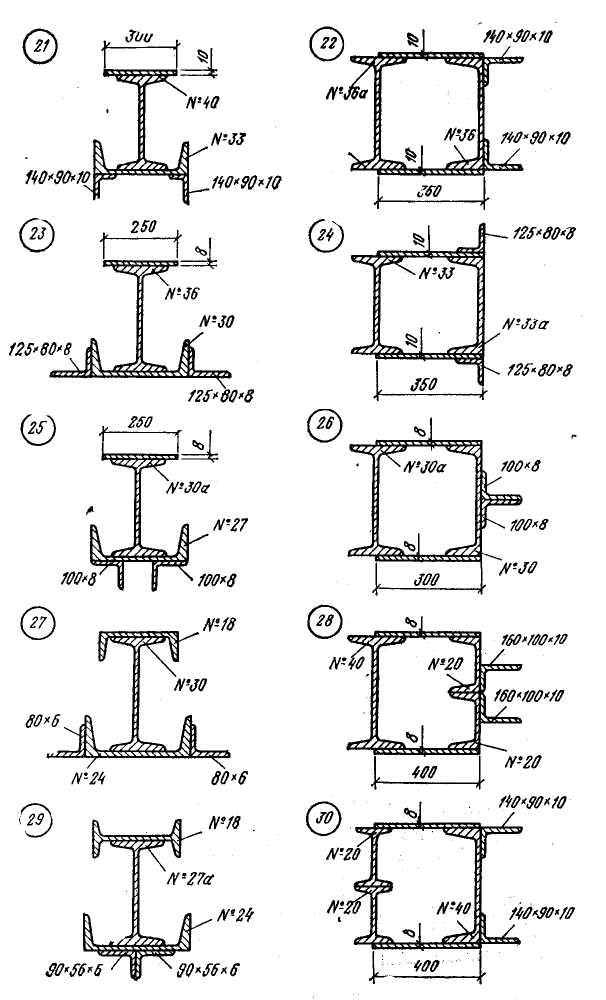
Рис. 2.1 в

3 Кручення брусу круглого поперечного перерізу

3.1 Теоретичні положення.

При крученні в поперечних перерізах брусу виникає тільки один внутрішній силовий фактор – момент кручення М_к. Зовнішні моменти, які викликали деформацію кручення, називають скручуючи ми, а брус, що працює на кручення, називають валом.

Крутячий момент на кожній ділянці вала визначається методом перерізів: М_к в будь-якому перерізі дорівнює алгебраїчній сумі зовнішніх моментів, прикладених по один бік від перерізу. При цьому приймається наступне правило знаків: зовнішній момент вважається додатним, якщо він діє проти годинникової стрілки при погляді з боку перерізу. Змінення крутячих моментів по довжині бруса зображують у вигляді епюри М_к. За епюрою визначають положення небезпечного перерізу.

Момент кручення викликає появу в перерізі дотичних напруг τ , які набувають найбільших значень в точках зовнішнього контуру перерізу. Умова міцності при крученні має вигляд:

τ_max = , (3.1)

де τ_max – максимальна дотична напруга в небезпечному перерізі, Н/мм²;

M_{к max} – максимальне значення крутячого моменту, Н∙мм;

W_p – полярний момент опору перерізу, мм³;

[ τ ] – допустима напруга при крученні, Н/мм².

Для круглого поперечного перерізу W_p = .

Для кільцевого поперечного перерізу W_p = .

Кут закручування вала на довжині l (взаємний кут повороту двох перерізів) визначається за формулою:

(3.2)

де М_к – крутячий момент на ділянці, Н∙мм;

l – довжина ділянки, мм;

G – модуль зсуву, Н/мм²;

I_p – полярний момент інерції перерізу, мм⁴.

Для круглого поперечного перерізу I_p= .

Для кільцевого поперечного перерізу I_p= .

Для сталі G = 8∙10⁴ Н/мм².

Розрахунки на жорсткість пов’язані з визначенням відносних кутів закручування φ₀ :

φ₀ = ,

а умова жорсткості має вигляд:

φ₀ = , (3.3)

де [φ₀] – допустимий кут закручування вала, рад.

За умовами міцності та жорсткості можна виконати проектний розрахунок вала, при якому визначаються потрібні діаметри поперечного перерізу.

Оскільки при розрахунках на кручення повинні виконуватись обидві умови (3.2) і (3.3), то остаточно приймається більший з обчислених діаметрів.

Аналогічно визначаються розміри кільцевого перерізу при заданому співвідношенні діаметрів c = d /D.