Уравнения математической физики

§ 1. Основные понятия теории уравнений математической физики

1⁰. Уравнение

(1)

где u - искомая функция, - независимые переменные , F – известная функция своих аргументов, называется дифференциальным уравнением в частных производных. Наивысший порядок частных производных, входящих в уравнение (1), называется порядком этого уравнения. Решением уравнения (1) в некоторой области D называется любая функция , необходимое число раз дифференцируемая и обращающая его в тождество.

Пример 1. Решить уравнение , где .

Решение. Исходное уравнение можно записать в виде , значит, производная зависит только от y, т.е. , где – произвольная дифференцируемая функция. Отсюда , где – произвольная дифференцируемая функция, зависящая только от x, а . Таким образом, решением рассматриваемого уравнения является любая функция вида , где и – произвольные дифференцируемые функции.□

Пример 2. Найти решение уравнения , удовлетворяющее условию .

Решение. Общее решение данного уравнения имеет вид . Подставим в полученное выражение , будем иметь . Отсюда . □

2⁰. Классификация линейных уравнений второго порядка. Рассмотрим уравнение

, (3)

1. Пусть в уравнении (3) – постоянные коэффициенты. Для того, чтобы привести уравнение (3) к каноническому виду применяют способ характеристик: составляется уравнение

, (4)

так называемое уравнение характеристик, которое распадается на два уравнения . Разделим уравнение (4) на и произведем замену , тогда уравнение (4) примет вид

. (5)

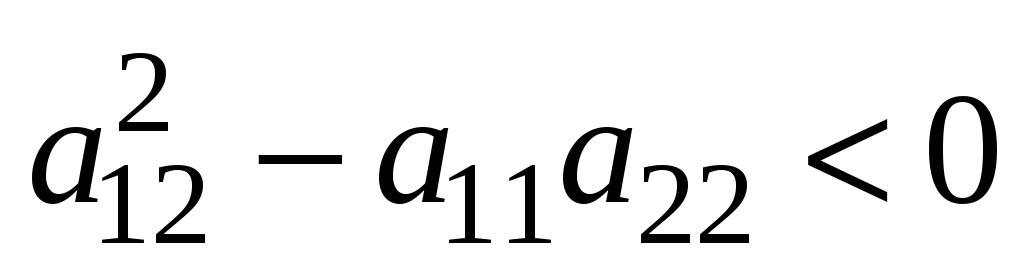1. Если , то уравнение эллиптического типа. Для этого уравнения интегралы уравнения характеристик имеют вид , где и – действительные функции. С помощью подстановки , уравнение (3) приводится к каноническому виду

,

где – новые переменные; – известная функция.

2. Если , то уравнение гиперболического типа. Тогда уравнение характеристик имеет два интеграла: , . С помощью замены переменных , дифференциальное уравнение (3) приводится к каноническому уравнению вида .

3. Если , то уравнение параболического типа. Тогда уравнение характеристик дает лишь один интеграл . В этом случае замена переменных 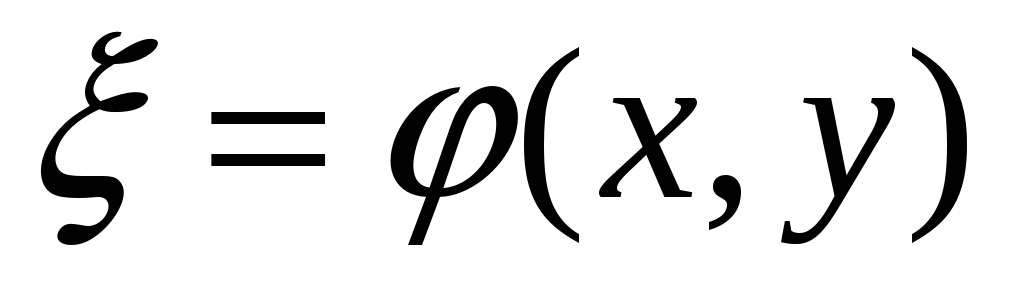, , где – некоторая функция, для которой . Тогда уравнение приводится к каноническому виду или , где ­– известные функции.

После указанных подстановок будем иметь уравнение

, (5)

где

Можно заметить, что для уравнений: 1) эллиптического типа , 2) гиперболического типа , 3) параболического типа или .

II. Если в уравнении (3) коэффициенты переменные, то для него выделяются области эллиптичности, гиперболичности и параболичности.

Пример 3. Привести к каноническому виду дифференциальное уравнение

.

Решение. В данном случае , , . Так как , то данное уравнение является уравнением гиперболического типа. Составим уравнение характеристик: . Оно распадается на два: , . Интегрируя их, соответственно получаем: , . Вводим новые переменные по формулам , . Вычислив , получим:

Подставив коэффициенты в уравнение (5), получим . □

Пример 4. Привести к каноническому виду уравнение .

Решение. Здесь , , , , т.е. имеем уравнение эллиптического вида. Уравнение характеристик запишется в виде: , получаем два семейства мнимых характеристик: и . Производя замену переменных , , имеемПодставив найденные значения в (5), получим . □

3⁰. Постановка задач для уравнений математической физики. В отличие от обыкновенных дифференциальных уравнений, для которых общее решение выражается через определенные функции, в случае уравнений в частных производных вид функций, через которые выражается их решение, не конкретизирован (с помощью одних только уравнений эти функции найти нельзя).

Для того, чтобы из бесчисленного множества решений дифференциального уравнения выделить частное решение, описывающее конкретный физический процесс, необходимо задать дополнительные условия. Обычно эти условия следуют из физической постановки задачи и физического смысла искомой функции. Чаще всего такими дополнительными условиями являются начальные условия (если искомая функция зависит от времени) и граничные (или краевые) условия. Начальные условия задают значение функции и определенного числа ее производных в начальный момент времени .

Различают три основных типа краевых задач математической физики.

1. Задача Коши для уравнений гиперболического и параболического типов: задаются начальные условия; область G, где происходит процесс, описываемый дифференциальным уравнением, есть пространство ; граничные условия отсутствуют.

2. Краевая задача для уравнений эллиптического типа: задаются граничные условия на границе S области G; начальные условия отсутствуют.

3. Смешанная задача для уравнений гиперболического и параболического типов: задаются и начальные, и граничные условия, .