
1. Скінченні поля на базі кілець класів лишків за даним простим модулем
Вище
як приклад скінченного поля розглядалося
кільце
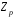 класів лишків цілих чисел за модулем
простого числа
класів лишків цілих чисел за модулем
простого числа
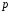 .
.
Арифметика над скінченними полями широко застосовується в криптографії і є основою багатьох криптосистем. Елементами таких полів є тільки скінченні числа, при операціях над якими відсутні похибки заокруглення.
Покажемо,
як перенести структуру поля з
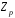 на множину без алгебраїчної структури.
на множину без алгебраїчної структури.
Для
простого числа
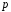 позначимо через
позначимо через
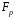 множину
множину
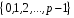 .
Визначимо відображення
.
Визначимо відображення
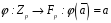 ,
де
,
де
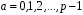 (
(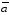 – класи лишків за модулем
– класи лишків за модулем
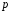 ).
Тоді множина
).
Тоді множина
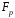 із
структурою поля, індукованою відображенням
із
структурою поля, індукованою відображенням
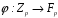 ,
також утворює скінченне поле, яке
називається полем
Галуа порядку
,
також утворює скінченне поле, яке
називається полем
Галуа порядку
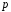 за ім’ям їх першого дослідника Еваріста
Галуа.
Таке
поле ще позначають
за ім’ям їх першого дослідника Еваріста
Галуа.
Таке
поле ще позначають
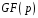 (
(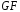 – Galois
Field
– поле Галуа).
– Galois
Field
– поле Галуа).
Відображення
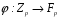 є ізоморфізмом,
оскільки
зберігає операції:
є ізоморфізмом,
оскільки
зберігає операції:
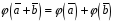 .
Нулем
скінченного поля
.
Нулем
скінченного поля
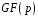 буде нуль 0,
а
одиницею – одиниця 1
і
його структура співпадає із структурою
поля
буде нуль 0,
а
одиницею – одиниця 1
і
його структура співпадає із структурою
поля
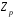 .
.
При
обчисленнях з елементами поля
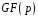 використовується арифметика цілих
чисел із зведенням за модулем
використовується арифметика цілих
чисел із зведенням за модулем
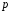 .
.
Приклад
3.
Найпростішим і найважливішим у
застосуваннях є поле
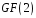 другого порядку з елементами
другого порядку з елементами
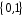 ,
для яких виконуються операції +
і
,
для яких виконуються операції +
і
 , визначені
таблицями Келі:
, визначені
таблицями Келі:
|
|
0 |
1 |
|
0 |
0 |
0 |
|
1 |
0 |
1 |
|
+ |
0 |
1 |
|
0 |
0 |
1 |
|
1 |
1 |
0 |
Приклад
4.
В полі Галуа
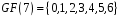 ,
яке ізоморфне скінченному полю
,
яке ізоморфне скінченному полю
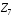 лишків цілих чисел за модулем 7, типові
арифметичні операції виглядають так:
лишків цілих чисел за модулем 7, типові
арифметичні операції виглядають так:
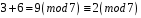 ,
,
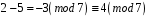 ,
,
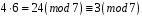 ,
,
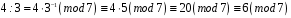 .
.
2. Характеристика поля
Скінченні
поля
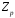 :
:
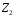 ,
,
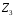 ,
,
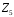 ,
…, посіли серед скінченних полів місце,
яке
можна зіставити з місцем, яке відведене
полю
раціональних чисел
,
…, посіли серед скінченних полів місце,
яке
можна зіставити з місцем, яке відведене
полю
раціональних чисел
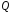 .
.
Означення. Поле, яке не має ніякого власного підполя, називається простим.
Теорема.
Кожне поле
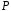 містить одне і тільки одне просте поле
містить одне і тільки одне просте поле
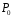 ,
яке ізоморфне або полю
,
яке ізоморфне або полю
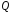 ,
або полю
,
або полю
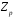 для деякого простого
для деякого простого
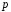 .
.
Доведення.
Припустимо,
що поле
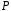 містить
два різних простих підполя
містить
два різних простих підполя
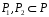 .
Тоді за
теоремою про переріз підполів
.
Тоді за
теоремою про переріз підполів
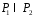 буде полем (очевидно, непорожнім, оскільки
0 і 1 містяться як в
буде полем (очевидно, непорожнім, оскільки
0 і 1 містяться як в
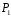 ,
так і в
,
так і в
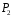 ),
відмінним від
),
відмінним від
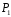 і
і
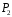 .
А це неможливо зважаючи
на
їх простоту. Отже, просте підполе
.
А це неможливо зважаючи
на
їх простоту. Отже, просте підполе
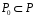 єдине. □
єдине. □
Означення.
Кажуть,
що поле
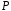 має характеристику
нуль,
якщо його просте підполе
має характеристику
нуль,
якщо його просте підполе
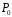 ізоморфне полю
ізоморфне полю
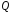 .
Кажуть, що поле
.
Кажуть, що поле
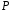 простої
(або скінченної) характеристики
простої
(або скінченної) характеристики
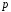 ,
якщо його просте підполе
,
якщо його просте підполе
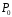 ізоморфне полю
ізоморфне полю
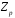 .
Відповідно пишуть
.
Відповідно пишуть
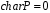 або
або
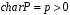 .
.
В
полі характеристики нуль всі елементи,
кратні одиниці поля, нерівні між собою,
тобто
 при
при
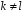 .
В полі скінченної характеристики існують
такі цілі числа
.
В полі скінченної характеристики існують
такі цілі числа
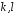 ,
,
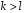 ,
що
,
що
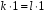 (або
(або
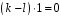 ).
Інакше: якщо одиниця поля є елементом
нескінченного порядку в адитивній групі
поля, то це поле має характеристику
нуль, а якщо одиниця поля – елемент
скінченного порядку – характеристика
в дорівнює порядку одиниці поля в
адитивній групі поля.
).
Інакше: якщо одиниця поля є елементом
нескінченного порядку в адитивній групі
поля, то це поле має характеристику
нуль, а якщо одиниця поля – елемент
скінченного порядку – характеристика
в дорівнює порядку одиниці поля в
адитивній групі поля.
Так,
числові поля раціональних, дійсних та
комплексних чисел мають характеристику
нуль, а будь-яке кільце
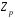 класів лишків цілих чисел за простим
модулем
класів лишків цілих чисел за простим
модулем
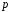 – це поле характеристики
– це поле характеристики
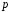 .
.
Приклад
5.
Поле Галуа
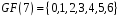 має
має
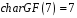 ,
тому що рівність
,
тому що рівність
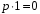 у цьому полі виконується при найменшому
додатному значенні
у цьому полі виконується при найменшому
додатному значенні
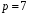 (тобто
(тобто
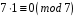 ).
).
Теорема
1.
В полі
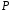 скінченної
характеристики
скінченної
характеристики
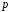 ,
для
будь-якого елемента
,
для
будь-якого елемента
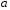 справджується рівність
справджується рівність
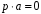 .
В полі
.
В полі
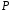 характеристики
нуль
для цілого числа
характеристики
нуль
для цілого числа
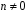 з
з
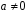 випливає
випливає
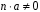 .
.
Доведення.
Згідно з означенням характеристики
поля, в першому випадку
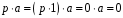 .
А в другому випадку, якби було справедливим
твердження
.
А в другому випадку, якби було справедливим
твердження
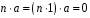 ,
то це означало б, що при
,
то це означало б, що при
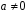 справджується рівність
справджується рівність
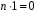 .
Через нульову характеристику поля
звідси виходить
.
Через нульову характеристику поля
звідси виходить
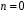 ,
що суперечить умові теореми. □
,
що суперечить умові теореми. □
Теорема
2.
Якщо
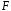 –
підполе
поля
–
підполе
поля
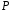 ,
то
,
то
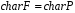 .
.
Справедливість теореми випливає з того, що одиниця поля є одиницею свого підполя.
Теорема
3.
Якщо
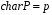 ,
то
,
то
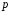 – просте число.
– просте число.
Наслідок. Характеристика скінченного поля – просте число.
Теорема
4.
Будь-яке скінченне поле
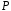 характеристики
характеристики
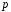 містить просте підполе з
містить просте підполе з
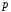 елементів і є скінченним розширенням
цього підполя.
елементів і є скінченним розширенням
цього підполя.
Теорема
5.
Нехай
 – скінченне поле характеристики
– скінченне поле характеристики
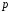 Тоді для довільних елементів
Тоді для довільних елементів
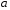 ,
,
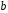 цього поля і для довільного
цього поля і для довільного
 справджуються рівності
справджуються рівності
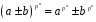 ;
;
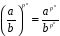 (
(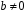 ).
).

