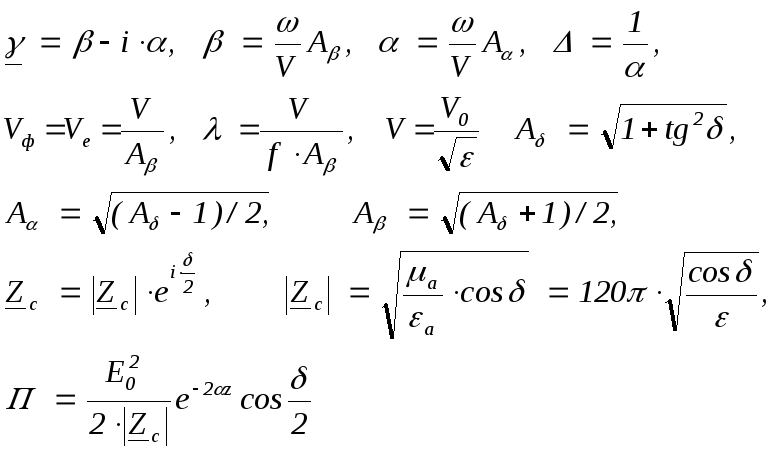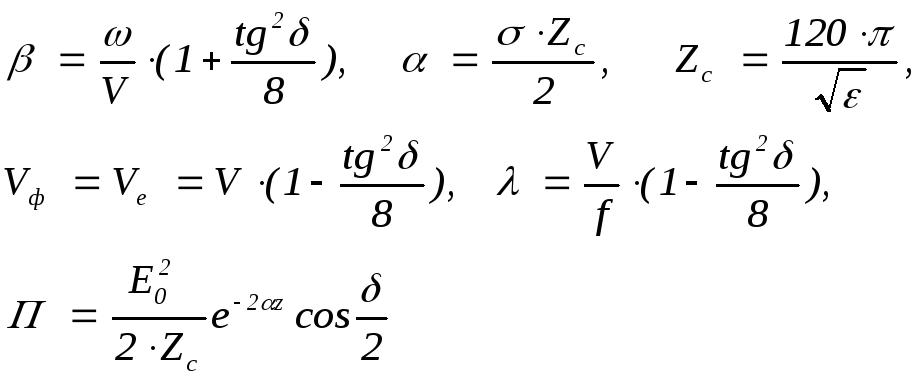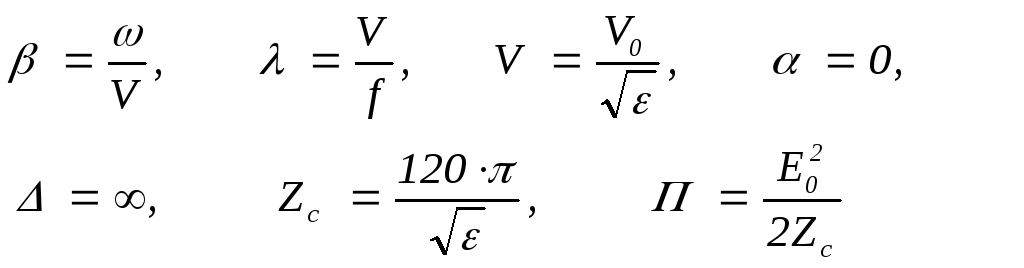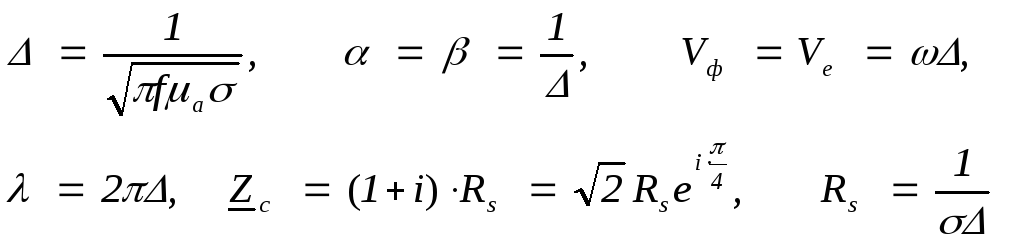2.5 Запитання та завдання до захисту індивідуального завдання 2

1. Пояснити методику знаходження повної енергії за № 2.1.

2. Як зміниться результат розрахунку в задачі № 2.2, якщо: а) зменшити вдвічі амплітуду; б) збільшити діелектричну проникність середовища; в) змінити розмір об'єму?

3. За № 2.3 пояснити невиконання принципу суперпозиції відносно енергії електромагнітного поля. Чому дорівнює взаємна енергія двох коливань ?

4. Дати фізичну трактовку вектора Пойнтинга за № 2.4.

5. Навіщо потрібні і чим відрізняються три записи вектора Пойнтинга в № 2.5?

6. Чому два результати за № 2.6 відрізняються між собою? Що вони означають?

7. Які втрати розраховані в № 2.7? Від чого залежить потужність втрат?

8. Назвіть значення добротності в № 2.7 зі збільшенням параметрів ,  в однакове число разів.

9. Назвіть рівняння, використане під час розв'язання задачі № 2.8.

10. Зобразити графіки залежності складових електромагнітного поля за № 2.9 для запропонованого варіанта резонансу.

3 Електромагнітні хвилі в необмеженому просторі

3.1 Стислі теоретичні відомості

Методика розв'язання хвильових рівнянь. Для випадку монохроматичного поля в необмеженому просторі хвильові рівняння (1.14) розв'язують з урахуванням початкових умов на початку вибраної системи координат. На початку координат приймають E = E₀cos(t–₀). У постановку задачі включають характеристики лінійного однорідного ізотропного немагнітного середовища: комплексну діелектричну проникність (1.12) при питомій провідністі 0    , магнітну проникність _а = ₀. Комплексні коефіцієнти (1.15) подають у вигляді

. (3.1)

Математичне розв'язання однорідних рівнянь (1.14) записується з точністю до сталих коефіцієнтів. Значення цих коефіцієнтів знаходять, прирівнюючи математичне розв'язання на початку координат значенню E = E₀cos(t–₀), а також виключаючи із розгляду варіанти розв'язань, що суперечать фізиці досліджуваних процесів. Для простоти приймають ₀ = 0.

Електромагнітні хвилі в лінійному однорідному ізотропному немагнітному середовищі. Введемо правогвинтову прямокутну систему координат і на початку координат орієнтуємо вісь x уздовж вектора електричного поля. Розв'язання хвильових рівнянь (1.14) мають вигляд

В / м, (3.2)

А / м, . (3.3)

Переходячи до реально існуючого поля, отримаємо

(3.4)

(3.5)

Виконаємо аналіз даного розв'язку, з'ясовуючи фізичні особливості і вводячи використовувані в електродинаміці терміни і визначення.

1. Співвідношення (3.2) – (3.5) описують хвилю, яка поширюється в конкретному напрямку (+z) без відбиття. Таку хвилю називають біжучою. Повне розв'язання хвильових рівнянь описує стоячу хвилю, утворену суперпозицією прямої хвилі, що поширюється в прямому напрямку (+z) і зворотної хвилі, що поширюється в зворотному напрямку (–z). Для зворотної хвилі в (3.2) – (3.5) необхідно змінити –z на +z.

2. За (2.7), (2.11) знаходимо середнє значення вектора Пойнтинга

. (3.6)

Енергія поширюється й експоненціально загасає в напрямку поздовжньої осі +z. При цьому густина потоку потужності залежить від кута втрат і зменшується зі збільшенням .

3. Комплексні амплітуди не залежать від поперечних координат x, y. Хвилю, у якої амплітуди не є функціями поперечних координат, називають однорідною. У неоднорідної хвилі амплітуди залежать від поперечних координат.

4. Вектори лежать у площині, перпендикулярній напрямку поширення хвилі. Таку хвилю називають поперечною. У поперечної хвилі вектори взаємоперпендикулярні: ²⁾.

5. Амплітуди електричного і магнітного полей зменшуються в напрямку поширення хвилі за експоненціальним заком , де , раз/м = неп/м  коефіцієнт загасання. Часто коефіцієнт загасання виражають в децибелах _дБ = 8,68. Величину, обернену коефіцієнту загасання

м , (3.7)

називають глибиною проникнення електромагнітного поля в середовище або глибиною скін-шару. Параметр  показує, на якій відстані електромагнітне поле ослаблюється в даному середовищі в e разів.

6. Фазові характеристики електромагнітної хвилі: (t–)  фаза, (t–z)  фаза електричного поля,  фаза магнітного поля;  фазові множники хвилі, яка поширюється в напрямку +z; t  зсув фази в часі, z  зсув фази у просторі, /2  зсув фази, обумовлений втратами; _е = z  зсув фази електричного поля, _м = z + /2  зсув фази магнітного поля. Принципово, що в середовищі з втратами зсув фази магнітного поля відносно електричного поля дорівнює /2.

Важливим параметром є коефіцієнт фази

(3.8)

де довжина хвилі  – відстань, на якій зсув фази дорівнює 2. Відповідно коефіцієнт фази визначає зсув фази на одиницю довжини. У формулі (3.1) комплексний коефіцієнт поширення виражений через коефіцієнт загасання  (уявна частина) і коефіцієнт фази  (дійсна частина).

7. У довільно обраній поперечній площині зсуви фази _е = z і _м = z + /2 будуть незмінними. Тобто поверхнею рівних фаз буде площина. В електродинаміці поверхню рівних фаз називають фронтом хвилі. Електромагнітні хвилі з пласким фронтом називають пласкими. Існують також циліндричні і сферичні хвилі.

8. В момент часу t₁ у перетині z₁ значення фази електричного поля дорівнює t₁–z₁. В момент часу t₂ знайдеться такий перетин z₂, що t₁–z₁ = t₂–z₂, або (t₂–t₁) = (z₂–z₁). За час t₂–t₁ фронт хвилі ніби змістився на відстань z₂–z₁. Швидкість руху фронту хвилі називають фазовою швидкістю

(3.9)

яка характеризує зміщення уявної поверхні рівних фаз і не пов'язана з рухом енергії.

9. Переміщення енергії в просторі характеризують швидкістю переносу енергії V_е. В необмеженому просторі V_ф = V_е.

10. Середовище і електромагнітну хвилю, яка поширюється в цьому середовищі, характеризують комплексним характеристичним опором – відношенням комплексних поперечних складових в режимі біжучої хвилі (БХ)

, Ом. (3.10)

В середовищі з втратами комплексний характеристичний опір пласкої однорідної хвилі

. (3.11)

Модуль комплексного характеристичного опору зростає зі збільшенням частоти і зі зменшенням  та . При зміні  від 0 до  значення змінюється від до 0, а аргумент /2  від 0 до /4.

11. Залежність характеристичного опору від частоти вказує на наявність фізичного явища, названого дисперсією. Електромагнітну хвилю називають дисперсною, а середовище  диспергуючим.

12. Формули (3.2)  (3.5) описують біжучу пряму однорідну поперечну пласку дисперсну електромагнітну хвилю. Співвідношення для розрахунку параметрів наведено у табл. 3.1. Видно, що при дисперсії від частоти залежать фазова швидкість, швидкість перенесення енергії та характеристичний опір.

Електромагнітні хвилі в діелектриках. Відповідно до табл. 1.2 існує три види діелектричних середовищ:

а) діелектрик з великими втратами  диспергуюче середовище. Формули для розрахунку параметрів носять загальний вигляд, наведені в першому рядку табл. 3.1, де для скорочення запису введені коефіцієнти A_α, A_β, A_δ , які пов'язані з коефіцієнтом загасання α, коефіцієнтом фази β і кутом втрат δ, відповідно;

б) діелектрик з малими втратами  середовище з незначною дисперсією. Формули трохи спрощуються (див. другий рядок табл. 3.1);

в) ідеальний діелектрик   = 0, tg = 0,  = 0. Формули набувають дуже простого вигляду. Наприклад

, (3.12)

де параметри характеризують вільний простір. Для вакууму та повітря  = 1.

Співвідношення (3.4) – (3.5) набувають вигляду

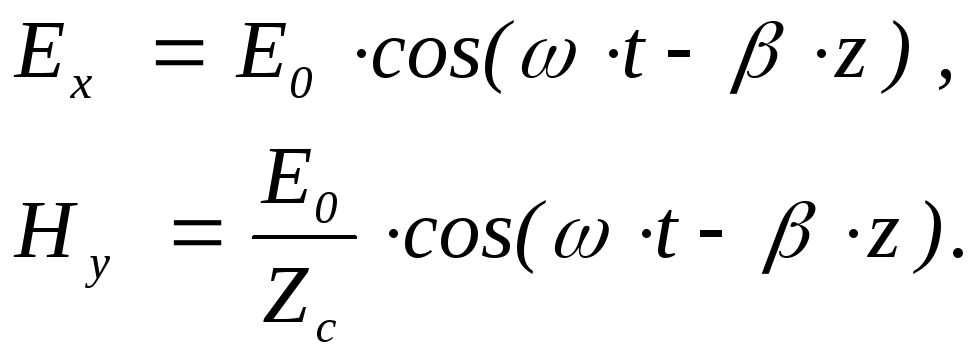(3.13)

Ця хвиля недисперсна, поширюється без загасання, а електричне і магнітне поле мають однакові фази.

Електромагнітні хвилі в провідниках. У провідниках tg  1. Формули, наведені в табл. 3.1, виражені через глибину скін-шару провідника .

Таблиця 3.1  Формули для розрахунку параметрів електромагнітних хвиль в

необмежених середовищах

Класифікація середовища за табл. 1.2		Формули
Значення tg	Найменування середовища
tg  1 (0,1 tg 10) (0  tg  )	Діелектрик з великими втратами, диспергуюче середовище
tg   1 (tg   0,1)	Діелектрик з малими втратами, середовище з незначною дисперсією
tg  = 0	Ідеальний діелектрик, недиспергуюче середовище
tg   1 (tg   10)	Провідник, диспергуюче середовище
tg   	Ідеальний провідник	. Поширення електромагнітних хвиль неможливе

Таблиця 3.2  Значення питомої провідності об'ємних металів і глибини скін-шару

Метал	 = 10-7, См/м)	, мкм на частоті
		1 ГГц	10 ГГц	30 ГГц
Ніхром	0,086	16,8	5,3	3,1
Манганін	0,217	10,8	3,4	1,97
Хром	0,476	7,3	2,3	1,33
Тантал	0,741	5,9	1,9	1,07
Молібден	1,75	3,8	1,2	0,69
Алюміній	3,57	2,7	0,84	0,48
Золото	4,17	2,5	0,78	0,45
Мідь	5,81	2,1	0,66	0,38
Срібло	6,25	2,0	0,64	0,37

^) Значення  отримані усередненням даних, наведених у різних джерелах. Питома провідність  = 10⁷ См/м.

Параметр

Ом (3.14)

називають поверхневим опором. У провіднику хвиля поширюється із значним загасанням, зсув фази магнітного поля відносно електричного максимальний і дорів -

нює /4. Пов'язано це з тим, що глибина проникнення поля в провідник дуже незначна (див. табл. 3.2) і, відповідно, малі значення V_ф, V_е,  і великі , . Складові електромагнітного поля

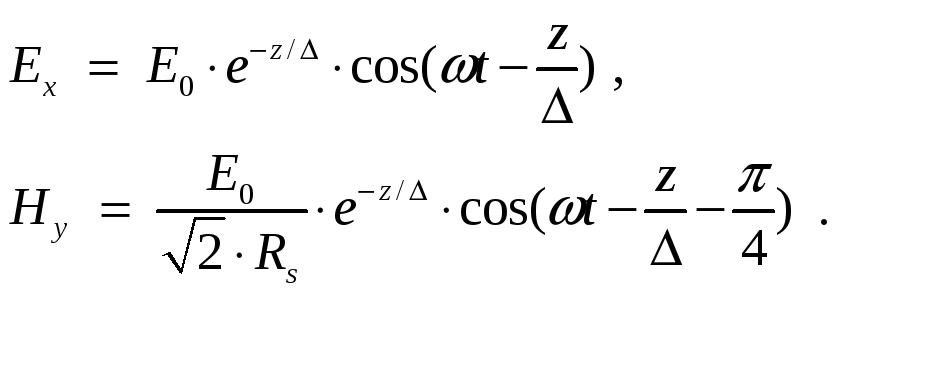(3.15)

В ідеальному провіднику поширення електромагнітних хвиль неможливе.

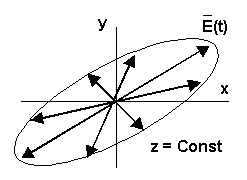
Поляризація електричного і магнітного полів. Електричне (або магнітне) поле має еліптичну поляризацію, якщо у фіксованій точці простору z = Const кінець вектора з плином часу описує еліпс (рис. 3.1). Якщо дивитися в напрямку поширення хвилі, то вектор може обертатися за годинниковою стрілкою (права поляризація ) або проти годинникової стрілки (ліва поляризація).

Окремими випадками еліптичної поляризації є лінійна поляризація, при якій одна з осей еліпса дорівнює нулю, і кругова поляризація, при якій осі

еліпса рівні.

Рисунок 3.1  Еліптична поляризація

Таблиця 3.3 – Дані для визначення виду поляризації

Вид поляризації	Співвідношення
	Амплітуд	Фаз
Лінійна	-
Колова
Еліптична

Вид поляризації залежить від зсувів фази проекцій вектора на поперечні осі і від амплітуд цих проекцій. Дані для визначення наведено у табл. 3.3. Підкреслимо, що види поляризації електричного і магнітного поля в однієї хвилі, як правило, неоднакові. Якщо не вказано поле (електричне чи магнітне), припускають поляризацію електричного поля.

Особливості електромагнітних хвиль з різними поляризаціями:

– поле хвилі з круговою або еліптичною поляризацією можна подати у вигляді суми двох взаємоперпендикулярних лінійно поляризованих хвиль;

– поле еліптично або лінійно поляризованої хвилі можна подати у вигляді суми двох хвиль з коловою поляризацією  правогвинтовою і лівогвинтовою;

– вид поляризації неоднорідної хвилі у різних точках поперечного перерізу може бути різним.

Класифікація та основні параметри електромагнітних хвиль. Узагальнимо стисло відомості про електромагнітні хвилі в необмежених середовищах. Класифікація хвиль наведена в табл. 3.4. Основні параметри, які описують електромагнітну хвилю, такі:

(3.16)

Таблиця 3.4 – Класифікація електромагнітних хвиль^*)

Характерна ознака	Назва електромагнітної хвилі
1. Відсутність відбиття	Біжуча
2. Напрямок поширення	Пряма або зворотна. Їх суперпозиція – стояча хвиля
3. Наявність векторів тільки в поперечному перетині	Поперечна
4. Форма фазового фронту	Пласка, циліндрична, сферична
5. Залежність амплітуди від поперечних координат	Однорідна або неоднорідна
6. Значення питомої провідності середовища	Дисперсна або хвиля без дисперсії
7. Співвідношення амплітуд і зсувів фаз проекцій векторів на поперечні осі системи координат	Лінійно поляризована, з коловою або з еліптичною поляризацією (табл. 3.3)

^*) Хвилі в обмежених середовищах класифікують аналогічно і характеризують такими самими параметрами. Але формули для розрахунку (3.16) залежать від умов поширення.

3.2 Ключові питання

1. Класифікація електромагнітних хвиль в необмеженому просторі.

2. Перелік, розмірність і фізичний зміст параметрів (3.16).

3. Визначення характеристичного опору.

4. Класифікація середовищ за значенням тангенса кута втрат.

5. Запис миттєвих значень складових електромагнітного поля в різних середовищах.

6. Особливості поширення електромагнітних хвиль в ідеальному діелектрику.

7. Особливості поширення електромагнітних хвиль в діелектрику із втратами.

8. Особливості поширення електромагнітних хвиль в провідниках.

9. Поляризація електромагнітних хвиль.