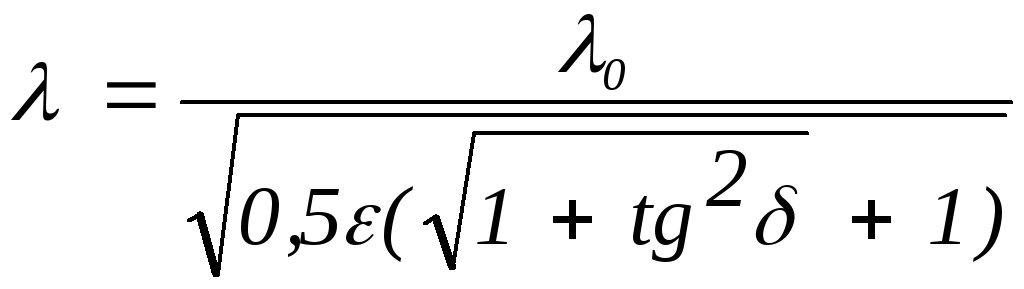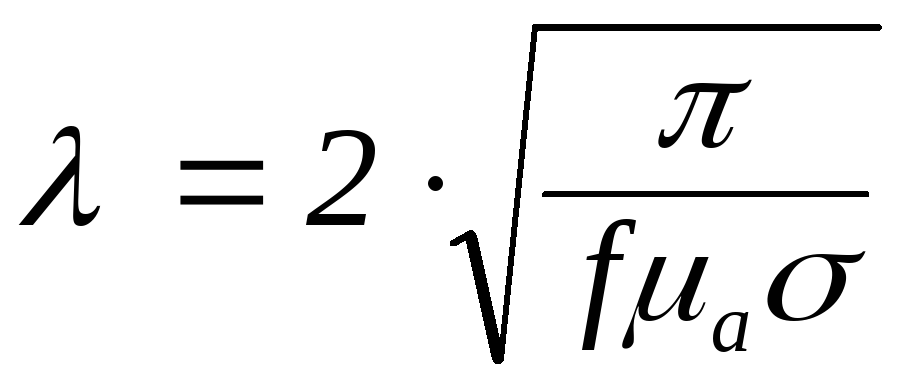1 Основні параметри середовищ. Вектори електромагнітного поля

 1.1 Стислі теоретичні відомості

Види частот і види радіохвиль. Межі видів частот та видів радіохвиль відрізняються на порядок. Їх найменування зведені в табл. 1.1. Частота f вимірюється в герцах (Гц), довжина хвилі  - в метрах (м).

У вакуумі , де V₀ = 2,9979·10⁸ м/с – швидкість світла.

Таблиця 1.1 - Найменування видів частот та видів радіохвиль за ДСТУ 325495^*)

Радіочастоти		Радіохвилі
Найменування	Межі f	Найменування	Межі 0
Дуже низькі частоти ДНЧ	3 - 30 кГц	Міріаметрові Мрм	10 - 100 км
Низькі частоти НЧ	30 - 300 кГц	Кілометрові км	1 - 10 км
Середні частоти СЧ	300 - 3000 кГц	Гектометрові гм	0,1 - 1 км
Високі частоти ВЧ	3 - 30 МГц	Декаметрові дам	10 - 100 м
Дуже високі частоти ДВЧ	30 - 300 МГц	Метрові м	1 - 10 м
Ультрависокі частоти УВЧ	300 - 3000 МГц	Дециметрові дм	0,1 - 1 м
Надвисокі частоти НВЧ	3 - 30 ГГц	Сантиметрові см	10 - 100 мм
Вельмивисокі частоти ВВЧ	30 - 300 ГГц	Міліметрові мм	1 - 10 мм
Гіпервисокі частоти ГВЧ	300 - 3000 ГГц	Дециміліметрові дмм	0,1 - 1 мм

^*) Рідко використовувані вельминизькі частоти ВНЧ 3 - 30 Гц, наднизькі частоти ННЧ 30 - 300 Гц та інфранизькі частоти ІНЧ 300 - 3000 Гц з розгляду виключені.

Основні параметри середовищ. В електродинаміці до основних параметрів середовища відносять абсолютну діелектричну проникність _а, Ф/м, абсолютну магнітну проникність _а, Гн/м, питому провідність , См/м. Для вакууму

(1.1)

В розрахунках використовують відносну діелектричну проникність  та відносну магнітну проникність  :

(1.2)

Для немагнітних середовищ _а = ₀. У вакуумі і у повітрі  = 1,  = 1.

За наявності електромагнітного поля, що змінюється з частотою, середовище характеризують тангенсом кута втрат

, де  = 2f – кругова частота. (1.3)

Теоретично кут втрат  змінюється від 0 до  / 2, а tg  – від 0 до  .

Класифікація середовищ. Лінійне середовище – середовище, в якому параметри _а, _а,  не залежать від напруженості електричного або магнітного поля. Однорідне середовище – середовище, в якому параметри _а, _а,  в усіх точках однакові. Ізотропне середовище – середовище, в якому параметри _а, _а,  не залежать від напрямку. Відповідно існують середовища нелінійні, неоднорідні, анізотропні. За винятком одного розділу, в навчальному посібнику розглядатимуть лінійні однорідні ізотропні немагнітні середовища.

Для змінного гармонічного або монохроматичного електромагнітного поля відрізняють середовища за значенням тангенса кута втрат (див. табл. 1.2). Ідеальний діелектрик та ідеальний провідник у природі не існують. Ці поняття використовують

Таблиця 1.2 – Класифікація середовищ за значенням tg 

Значення tg 	Найменування середовища	Формула для розрахунку 
tg  = 0	ідеальний діелектрик (діелектрик без втрат)
tg   1 (tg   0,1)	діелектрик з малими втратами
tg  ~ 1 (0,1  tg   10)	діелектрик з великими втратами
tg   1 (tg   10)	провідник
tg   	ідеальний провідник	 = 0

для простоти моделювання процесів у середовищах з дуже малими втратами або у провідниках з tg   , що полегшує виконання розрахунків.

Зазначимо, що в ідеальному діелектрику довжина хвилі менша довжини хвилі у вакуумі, для діелектриків з втратами  залежить від  і від . В провідниках  залежить від , а в ідеальному провіднику змінне електромагнітне поле не існує.

Вектори електромагнітного поля. Електромагнітне поле характеризують чотири вектори:

– вектор напруженості електричного поля , В/м;

– вектор напруженості магнітного поля , А/м;

– вектор електричного зміщення , К/м²;

– вектор магнітної індукції , Вб/м².

Цим векторам відповідають скалярні величини: напруженість електричного поля E, напруженість магнітного поля H, електричне зміщення D (електрична індукція), магнітна індукція B.

Рівняння Максвелла. Повна система рівнянь Максвелла описує всі можливі електромагнітні процеси. В диференціальній формі ця система записується так:

де – вектор густини повного струму, А/м², – вектор густини струму провідності, – вектор густини струму зміщення,  – об'ємна густина електричного заряду, t – час.

У системі (1.4) рівняння (1РМ) – (4РМ) являють собою безпосередньо рівняння Максвелла, (5РБ) – т. з. рівняння неперервності, (6МР) – (8МР) – матеріальні рівняння, а (9Р) – рівняння, записані для пояснення фізичного змісту .

Фізичний зміст рівнянь Максвелла. В першому рівнянні Максвелла (1РМ) операція rot (ротор) у перекладі означає "обертання", "вихор". Тобто ротор (обертання) вектора магнітного поля є джерелом повного струму, вектор густини якого складається з суми векторів густини струму провідності та густини струму зміщення – див. (8МР) – (9Р).

З другого рівняння Максвелла (2РМ) випливає, що обертання вектора електричного поля пов'язано зі швидкістю зміни магнітної індукції, спрямованої у протилежний бік.

Третє (3РМ) і четверте (4РМ) рівняння Максвелла містять операцію div (дивергенція), в перекладі "розбіжність". Розбіжність вектора електричного змыщення дорівнює   0, тобто лінії і обов'язково мають початок і кінець. Навпаки, розбіжність вектора магнітної індукції дорівнює нулю, тобто лінії і завжди замкнені. З (4РМ) випливає ще один важливий висновок: у природі не існує магнітних зарядів (у правій частині знаходиться рівна нулю об'ємна густина магнітного заряду).

Для пояснення фізичного змісту рівняння (5РБ) запишемо

(1.5)

Розбіжність вектора повного струму дорівнює нулю: лінії завжди замкнені, а лінії і мають початок (витік) та кінець (стік).

Основні наслідки з системи рівнянь (1.4). Можна виділити п'ять основних наслідків, що випливають із рівнянь Максвелла (1РМ) – (4РМ).

1. Для кожного з чотирьох векторів електромагнітного поля виконується т. з. принцип суперпозиції: сумарний вектор дорівнює сумі векторів усіх m джерел

, (1.6)

2. При постійному струмі вектори електромагнітного поля не змінюються в часі. Система (1.4) описуватиме електромагнітне поле постійного струму, якщо в рівняннях (1РМ), (2РМ), (5РБ), (9Р) порівняти з нулем всі похідні за часом.

3. Якщо другий наслідок доповнити відсутністю постійного струму (), система (1.4) розіб'ється на дві незалежні і незв'язані системи, одна з яких описує електростатику, а інша – магнітостатику.

4. Для опису квазістаціонарних процесів, для яких характерна повільна зміна в часі, в першому рівнянні Максвелла (1РМ) і в (9Р) за наявності струму провідності . В іншому випадку .

5. Основу електродинаміки становить змінне за часом електромагнітне поле . З (1.4) випливає:

– будь-яка зміна напруженості електричного поля спричинює зміну напруженості магнітного поля і навпаки (див. (1РМ) – (2РМ));

– не можуть існувати незалежно один від одного, створюючи єдине змінне електромагнітне поле (див. також (1РМ) – (2РМ));

– для провідників, для діелектриків (див. (1РМ), (9Р));

– змінне електромагнітне поле є джерелом виникнення перемінних струмів провідності і зміщення з густинами ,, та навпаки, змінні струми провідності або зсуву є джерелом появи змінних (див. (1РМ) – (2РМ)).

Метод комплексних амплітуд. У випадку змінного електромагнітного поля для спрощення математичних викладок і фізичного аналізу процесів користуються методом комплексних амплітуд. Так, замість запису гармонічного монохроматичного поля

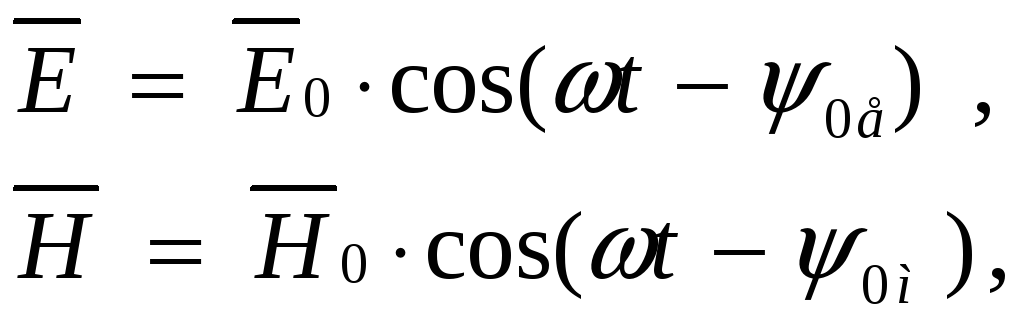(1.7)

(  амплітуди,  початкові зсуви фази електричного та магнітного поля) подають у комплексному вигляді

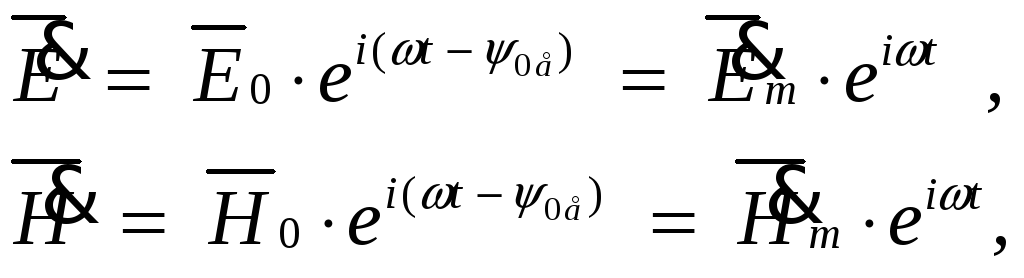(1.8)

припускаючи

(1.9)

Щоб взяти похідну за часом достатньо помножити вихідну функцію на i:

, (1.10)

а щоб взяти інтеграл – помножити на 1/ i.

Для подання складних записів монохроматичних (одночастотних) полів у комплексному вигляді необхідно звести їх до запису (1.8), використуючи математичні формули перетворення синусоїдальних величин. Приклад:

u = a · sint + b · cost = A · sin(t + ) = A · cos(t +  - /2), (1.11)

.

Рівняння Максвелла для монохроматичного поля. Перетворимо перше рівняння Максвелла (1РМ) з урахуванням (1.10), (6МР), (8МР), (9Р):

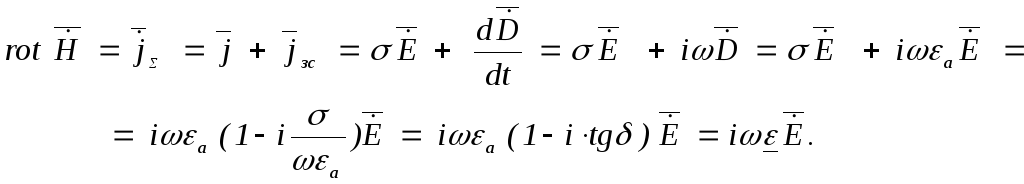
Такі самі викладки можна зробити і для другого рівняння Максвелла (2РМ). Параметр

(1.12)

зветься абсолютною комплексною діелектричною проникністю. Активна частина комплексної діелектричної проникності дорівнює _а = ₀, а реактивна пов'язана із втратами в середовищах і має значення  _а tg.

Система (1.4) зводиться до системи з двох рівнянь:

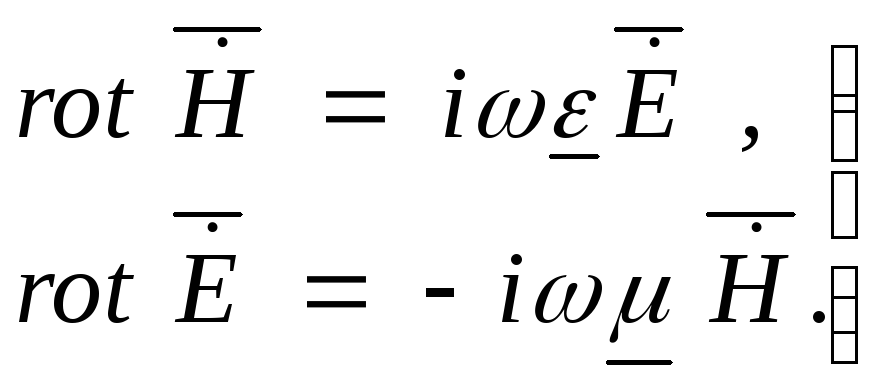(1.13)

В (1.13) для немагнітних середовищ .

Хвильові рівняння для монохроматичного поля. Система (1.13) містить два рівняння з двома невідомими у кожному. Поставимо задачу перетворення (1.13) для одержання двох рівнянь з одним невідомим у кожному. Візьмемо rot від обох частин першого рівняння.

Ліва частина: , де – оператор Лапласа.

Права частина: .

Для другого рівняння в (1.13) можна виконати аналогічні операції. У результаті отримуємо

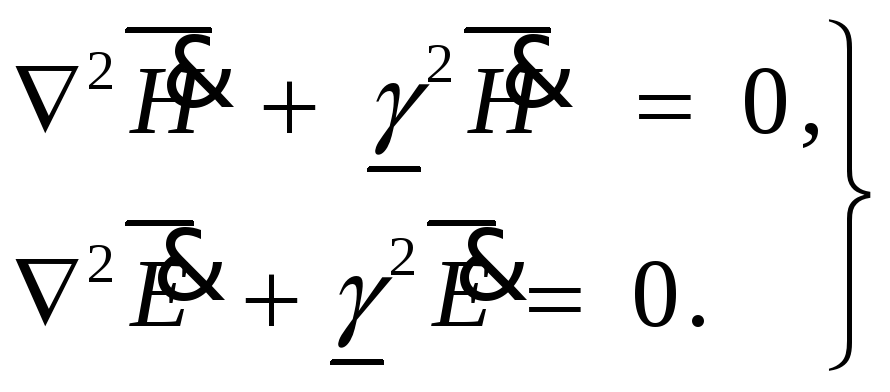(1.14)

В математиці рівняння (1.14) називають однорідними рівняннями Гельмгольца, а в електродинаміці – хвильовими рівняннями для монохроматичного поля. Параметр

(1.15)

називають хвильовим числом, а – комплексним коефіцієнтом поширення.

1.2 Ключові питання

1. Види частот і види радіохвиль.

2. Основні параметри середовищ.

3. Абсолютні і відносні діелектрична і магнітна проникності.

4. Поняття лінійного однорідного ізотропного середовища.

5. Діелектрики і провідники. Тангенс кута втрат.

6. Методика розрахунку довжини хвилі в різних середовищах.

7. Вектори електромагнітного поля, їх розмірність.

8. Фізичне трактування повної системи рівнянь Максвелла.

9. Основні наслідки з системи рівнянь Максвелла.

10. Сутність методу комплексних амплітуд.

11. Рівняння Максвелла для монохроматичного поля.

12. Хвильові рівняння для монохроматичного поля.