Додаток б Модифікований алгоритм Ейлера

Припустимо , , – радіус-вектор, вектор швидкості та вектор прискорення в момент часу . – рівнодіюча сила, яка діє на матеріальну точку. Тоді рух матеріальної точки маси m можна описати за допомогою рівняння динаміки

. (Б.1)

Згідно з (Б.1) рух точки для моментів часу визначено однозначно, якщо відомо початковий стан точки в момент часу (початкове положення та початкова швидкість ). Розглянемо наближені кінематичні формули:

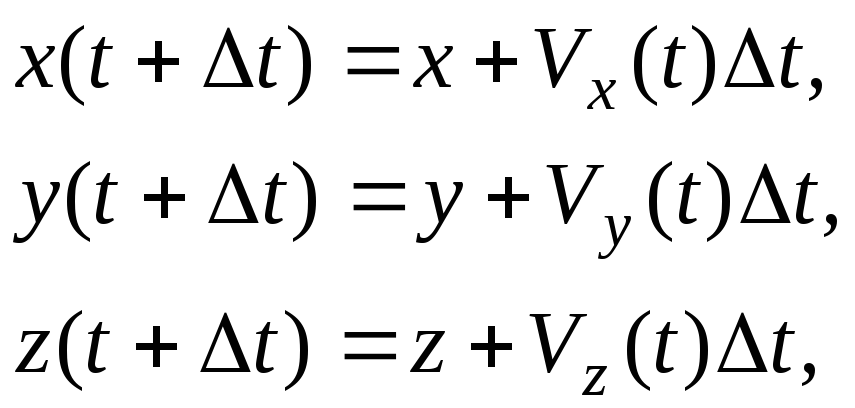
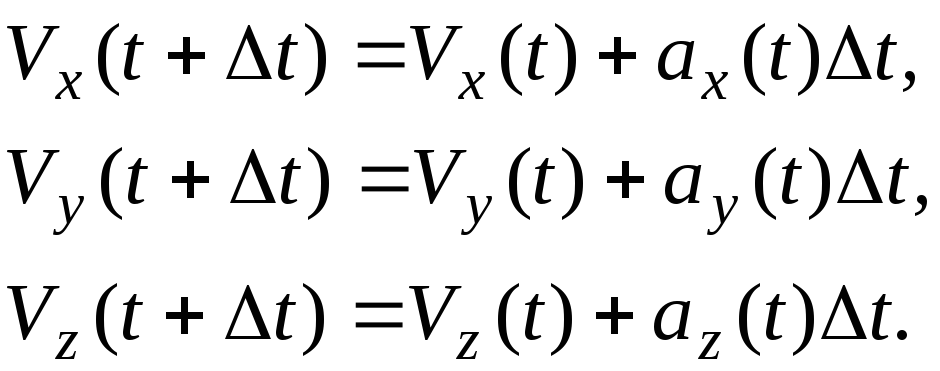(Б.2)

З формул (Б.2) випливає, що положення та швидкість точки в момент часу можна обчислити, якщо відомі її положення, швидкість та прискорення в момент t, завданням початкового стану в момент t, а прискорення – з динамічного рівняння Ньютона (Б.1)

, , . (Б.3)

Отже, послідовно застосовуючи (Б.2) і (Б.3), можна визначити положення точки в будь-який момент часу.

Оскільки схема Ейлера має похибку обчислень ~ , то для її зменшення застосовується модифікований метод Ейлера – коефіцієнти виразів (Б.2) (значення швидкості та прискорення підставляються в момент часу, який відповідає середині інтервалу , тобто в момент . При цьому похибка розрахунків за формулами (Б.2), (Б.4) має порядок . Така видозмінена схема називається модифікованим методом Ейлера.

Додаток в Визначення ймовірної швидкості молекул

Згідно з [4] функції розподілу складових , швидкості молекули на площині XOY мають такий вигляд:

,

,

де m – маса молекули, T – абсолютна температура газу, k – стала Больцмана.

Ймовірність того, що швидкість деякої молекули має значення в межах , , , визначатиметься за формулою

Рисунок В.1

,

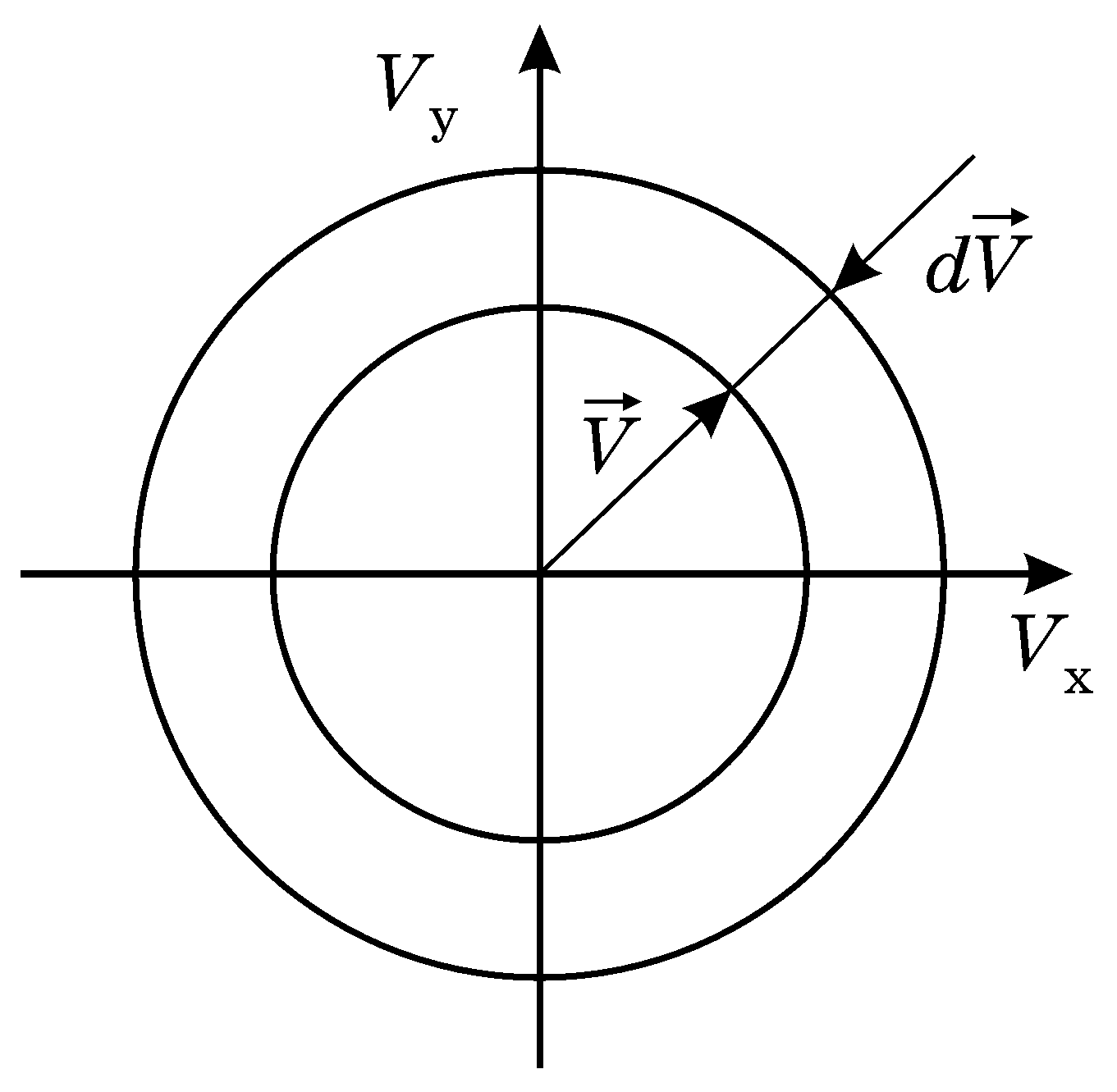
де , згідно з рис.В.1, дорівнює .

Отже, функція розподілу, яка характеризує ймовірність того, що величина швидкості знаходиться в межах

.

Ймовірну швидкість можна тоді знайти за умови максимуму функції

. (В.1)

Розв’язуючи рівняння (В.1), маємо .

В тривимірному випадку, аналогічний розрахунок, як відомо, дає результат

.

3