Элементарная геометрия 2

Пирамида

1. В основании пирамиды лежит прямоугольный треугольник с катетами 6 и 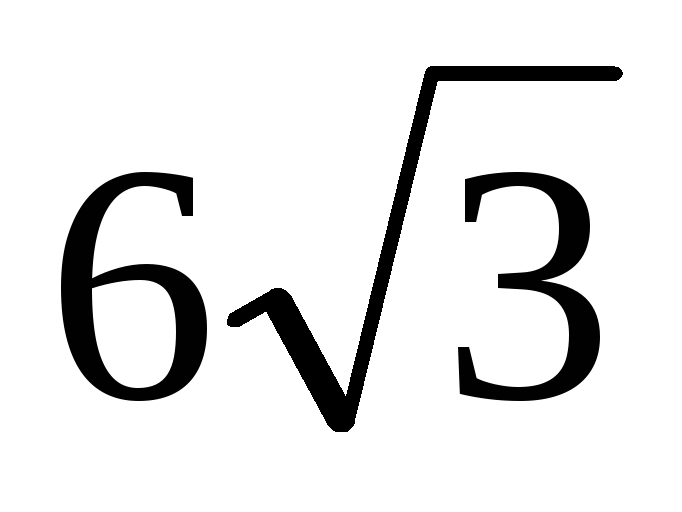. Боковые рёбра пирамиды наклонены к плоскости основания под углом 30°. Вычислите объём пирамиды.

2. Основание пирамиды — треугольник, две стороны которого равны 3 и 6 и образуют угол в 60°. Боковые рёбра наклонены к плоскости основания под одним и тем же углом. Найдите объём пирамиды, если боковое ребро равно .

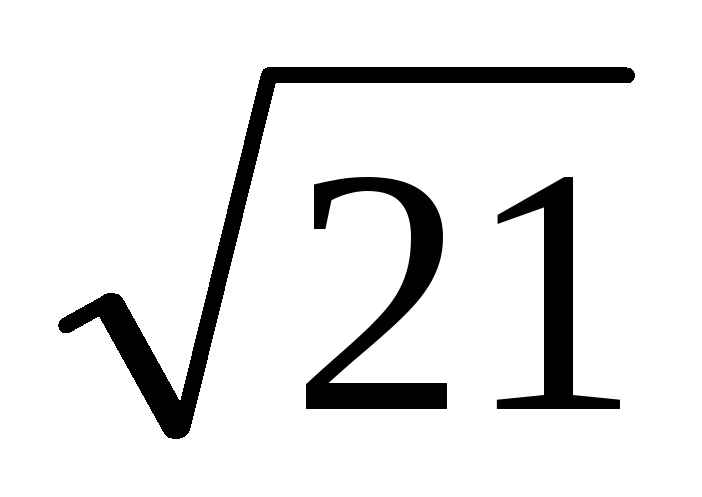3. Основание пирамиды — равнобедренный треугольник, боковые стороны которого равны 6 и образуют угол в 120°. Боковые рёбра наклонены к плоскости основания пирамиды и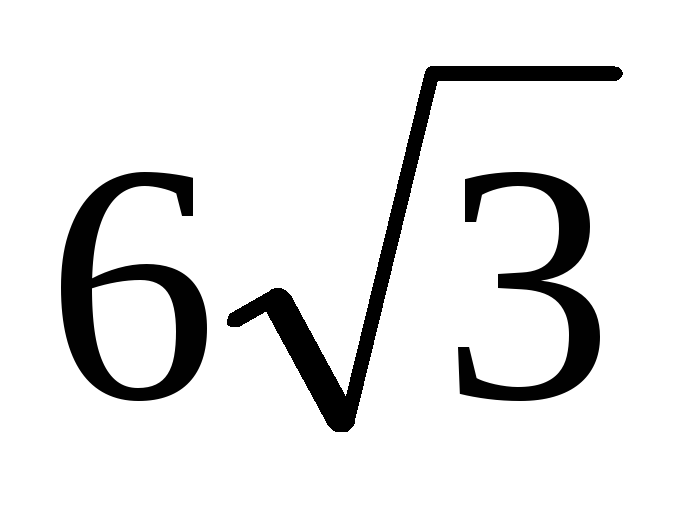под одинаковым углом. Найдите объём пирамиды, если боковое ребро равно .

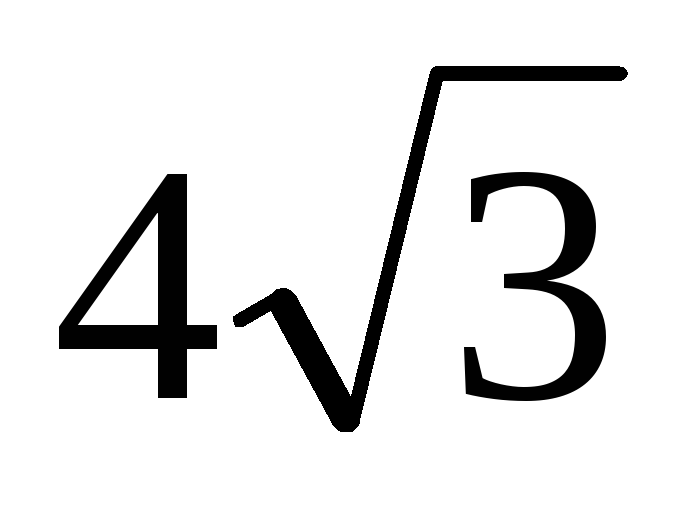4. Основание пирамиды — прямоугольный треугольник с катетами б и 8. Боковые грани составляют с плоскостью основания равные углы α, причём tgα = 3. Найдите объём пирамиды.

5. Правильная треугольная пирамида рассечена плоскостью, перпендикулярной основанию и делящей две стороны основания пополам. Найдите площадь сечения пирамиды этой плоскостью, если известно, что сторона основания равна 2, а высота пирамиды равна 24.

6. Основание пирамиды — прямоугольный треугольник с катетами 6 и 8. Все двугранные углы при основании пирамиды равны 60°. Найдите площадь боковой поверхности пирамиды.

7. Высота правильной треугольной пирамиды равна 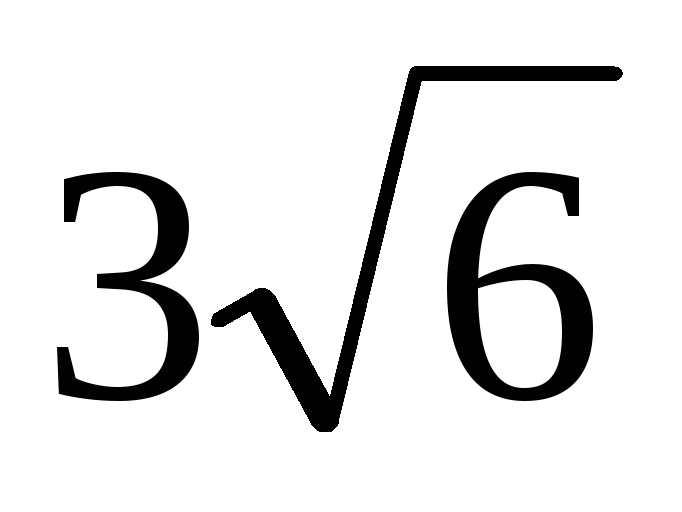, а двугранный угол, образованный боковыми гранями, равен 120°. Найдите длину стороны основания.

8. В основании треугольной пирамиды SABC лежит правильный треугольник ABC. Боковое ребро пирамиды SA перпендикулярно плоскости основания. Найдите объём пирамиды, если величина угла между прямой SA и прямой, проходящей через точку С и середину ребра SB, равна 60°, а расстояние между этими скрещивающимися прямыми равно .

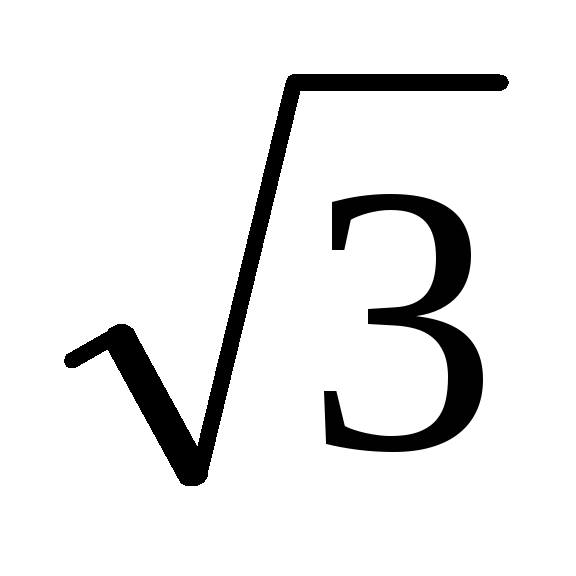9. В правильной треугольной пирамиде SABC, где S — вершина, сторона основания равна 12. Найдите объём пирамиды, если площадь сече­ния пирамиды плоскостью, проходящей через вершину S и середины рё­бер АВ и АС, равна .

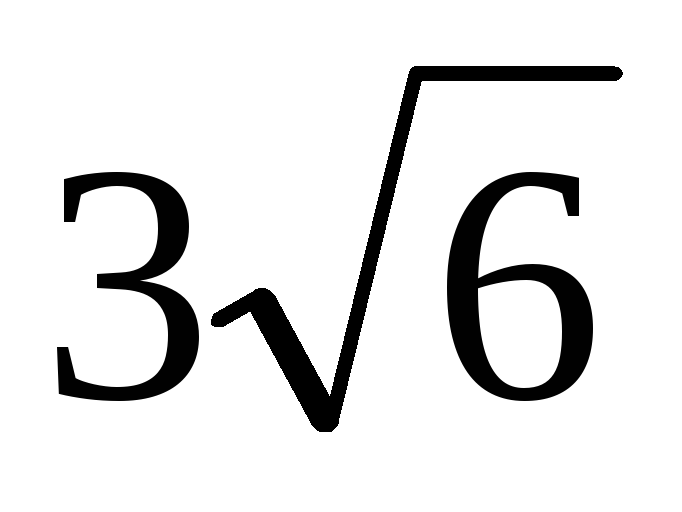10. Сторона основания правильной четырёхугольной пирамиды SABCD, где S — вершина, равна 8. Найдите расстояние между прямыми, содержащими рёбра CD и SB, если высота пирамиды равна 3.

11. Сторона основания правильной четырёхугольной пирамиды равна 2. Найдите расстояние между прямыми, содержащими диагональ основания и высоту боковой грани, если высота пирамиды равна .

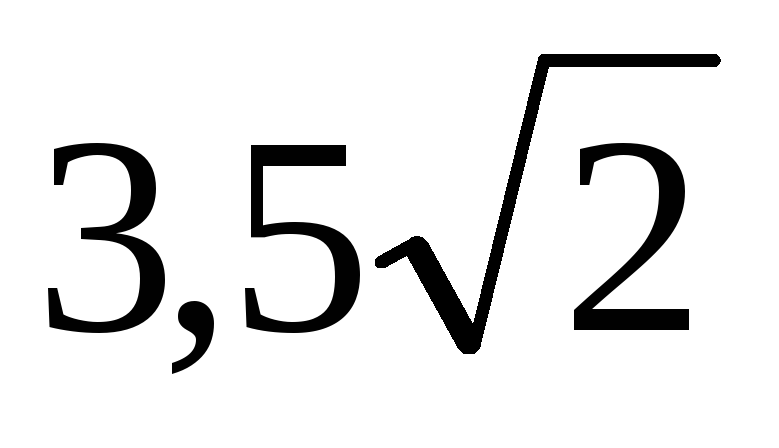12. Основание пирамиды — прямоугольный треугольник с катетами 5 и 12. Все двугранные углы при основании пирамиды равны 30°. Найдите 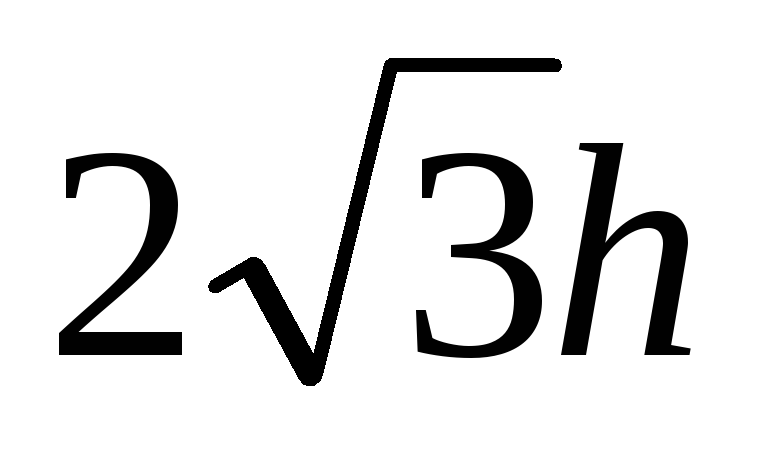, где h — высота пирамиды.

13. В равнобедренном треугольнике угол при вершине равен 120°. Точ­ка, удаленная от вершин этого треугольника на расстояние 35, удалена от плоскости треугольника на расстояние 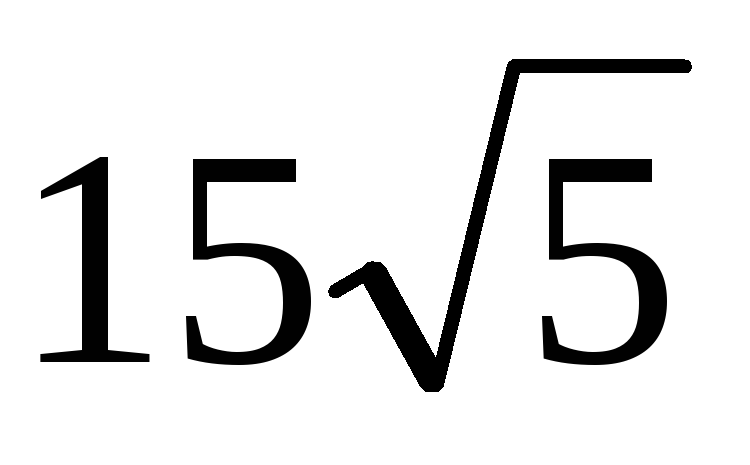. Найдите боковую сторону равнобедренного треугольника.

14. Дана правильная четырёхугольная пирамида со стороной основания 10. Боковая грань удалена от центра основания на расстояние 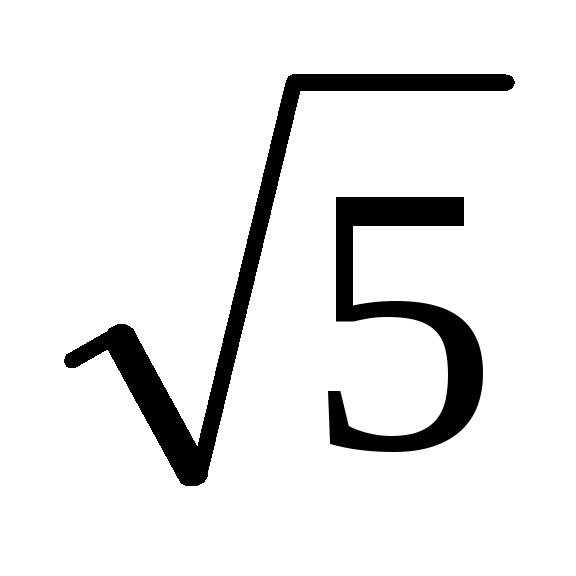. Найдите длину бокового ребра пирамиды.

15. В правильной треугольной пирамиде DABC сторона основания рав­на 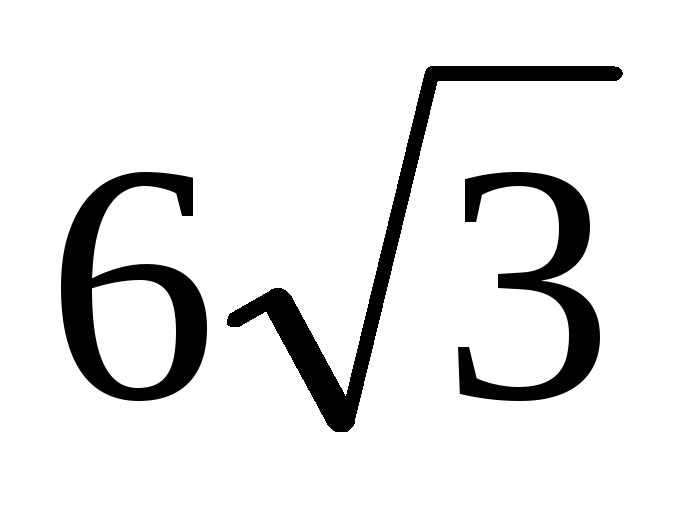, а высота DH пирамиды, опушенная из вершины D на плоскость основания ABC, равна 4. Найдите расстояние от точки D до плоскости, проходящей через точку Н параллельно плоскости DBC.

16. Высота правильной четырёхугольной пирамиды равна 10, а площадь сечения, параллельного боковой грани и проходящего через центр осно­вания, равна 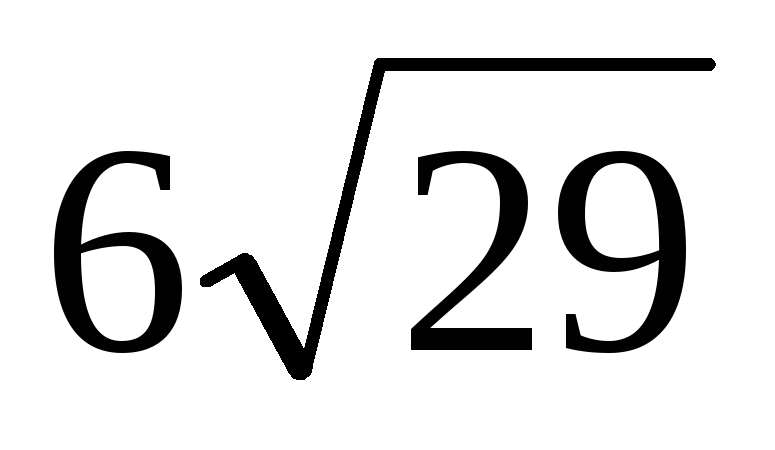. Найдите сторону основания пирамиды.

17. В правильной треугольной пирамиде боковое ребро наклонено под углом φ к плоскости основания. Найдите расстояние между боковым реб­ром и серединой противоположной стороны, если объём пирамиды равен 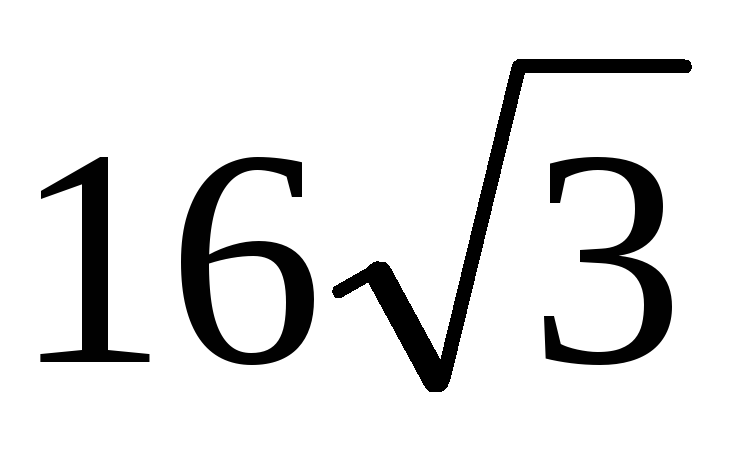и cosφ = 1\3.

18. Угол между высотой правильной треугольной пирамиды и апофемой пирамиды равен φ. Найдите дайну высоты пирамиды, если соsφ = 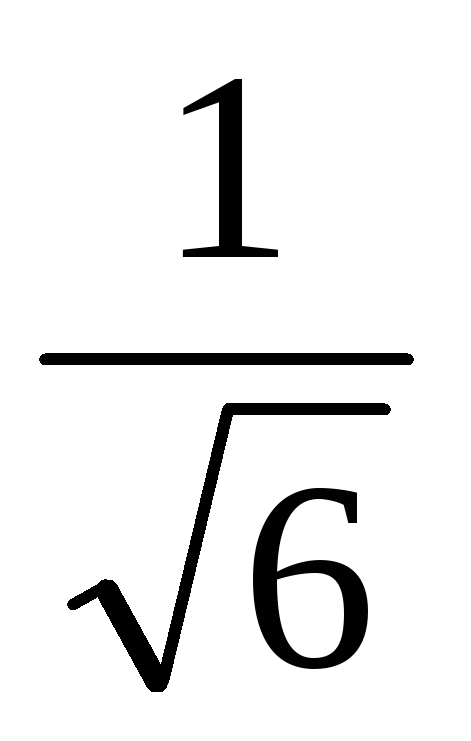объем пирамиды равен.

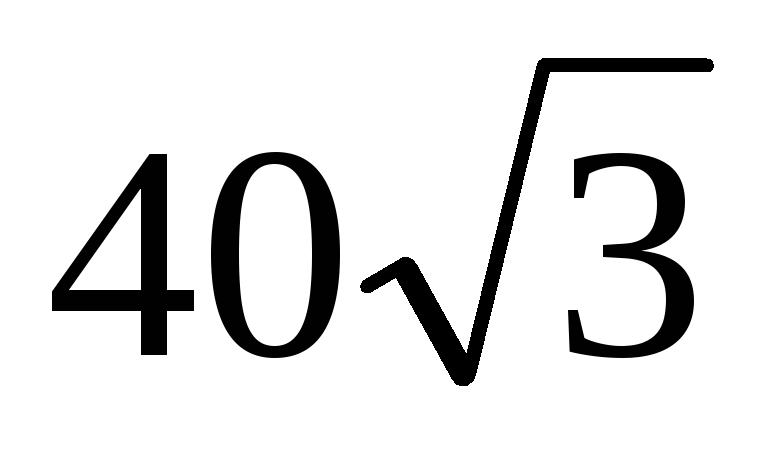19. Плоскость делит треугольную пирамиду на два многогранника. Во сколько раз объем большего из многогранников превосходит объём меньшего, если известно, что секущая плоскость делит три ребра, выходящие из одной вершины пирамиды в отношении 1 : 3, 1 : 4 и 2 : 3, считая от вершины.

20. В правильной треугольной пирамиде SABC ребро SA наклонено к плоскости основания ABC под углом α. Найдите расстояние от середины ребра SA до прямой ВС, если cosα = 1/3, сторона основания пирамиды равна 6.

21. В правильной треугольной пирамиде SABC ребро SA наклонено к плоскости основания ABC мод углом α. Найдите сторону основания пирамиды, если cosα = 1/3, а расстояние от середины ребра SB до прямой АС равно 12.

22. В правильной треугольной пирамиде SABC ребро SA наклонено к плоскости основания ABC под углом 30°. Точка К делит ребро SA в отношении 1 : 3, считая от вершины S. Найдите площадь треугольника КВС, если сторона основания пирамиды равна 7.

23. В правильной треугольной пирамиде SABC ребро SB наклонено к плоскости основания ABC под углом 30°. Точка К делит ребро SA в отношении 1 : 3, считая от вершины S. Найдите расстояние от точки К до прямой ВС, если площадь треугольника КВС равна 36.

24. В пирамиде SABC - SA = 4, SB = 5, ABC = 150°. Найдите расстояние между прямыми AS и ВС, если известно, что SA — перпендикуляр к плоскости основания АВС.

25. В треугольной пирамиде АBCD ребро AD перпендикулярно грани BCD и равно 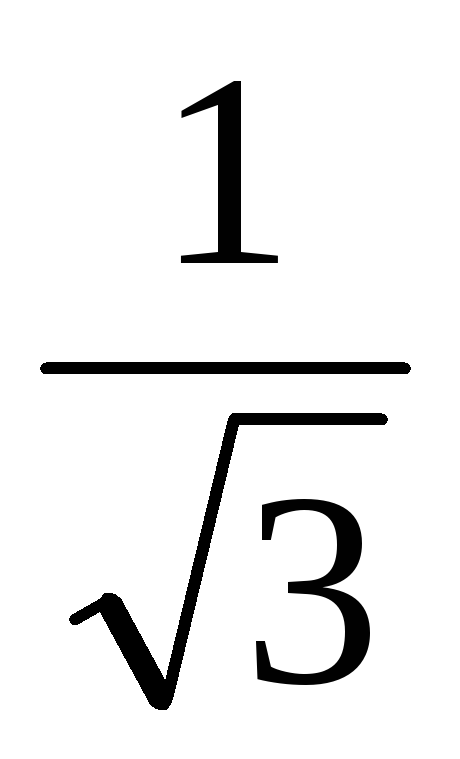, а грань BCD является равнобедренным треугольником, в котором BD = CD = 4, ВС = 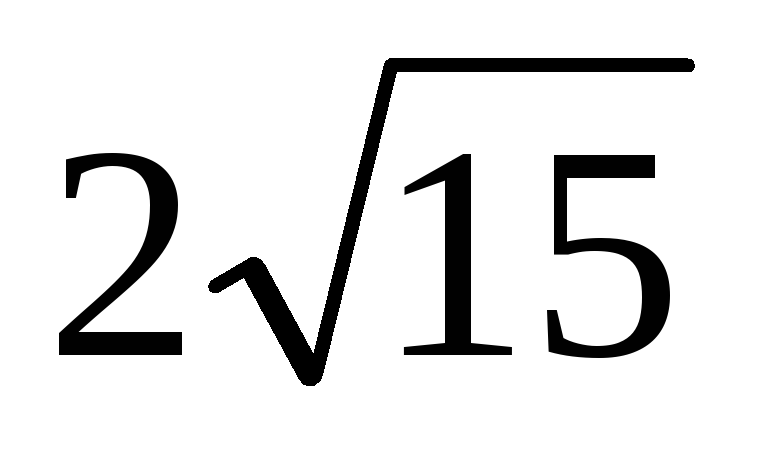. Найдите градусную меру угла между рёбрами CD и АВ.

26. В основании пирамиды SAВCD лежит параллелограмм ABCD, SA=SD=SC=15, SB — высота пирамиды. Тангенс угла наклона между прямой SD и плоскостью основания пирамиды равен 0,75. Найдите, периметр основания пирамиды.

27. SB — высота пирамиды SABCD, в основании которой лежит параллелограмм ABCD, а косинус угла между прямыми АВ и SC равен 0,4 , SA = SC = 15, АВ = 12. Найдите тангенс угла между прямой SD плоскостью основания.

28. SB — высота пирамиды SABCD, в основании которой лежит па­раллелограмм ABCD, SA = SC = 20, АВ = 16, а тангенс угла между прямой SD и плоскостью ABC равен 0,75. Найдите косинус угла между прямыми SC и АВ.

29. В правильной треугольной пирамиде сторона основания равна 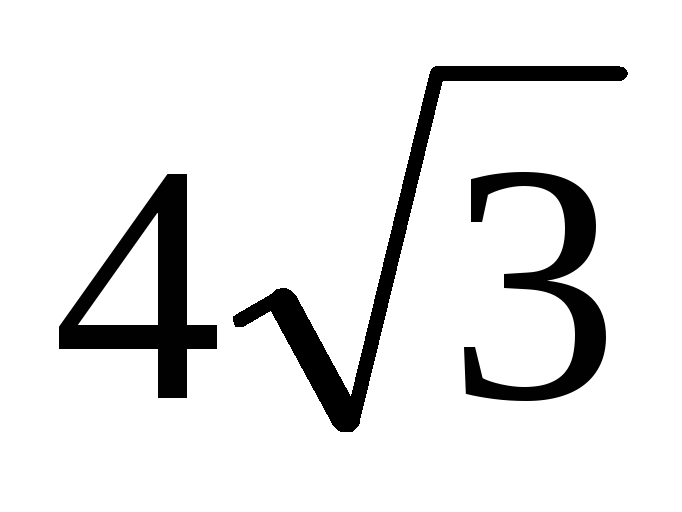. Через вершину основания проведено сечение, параллельное противопо­ложной стороне основания и перпендикулярное противоположной боко­вой грани пирамиды. Сечение наклонено к плоскости основания пирамиды под углом, тангенс которого равен 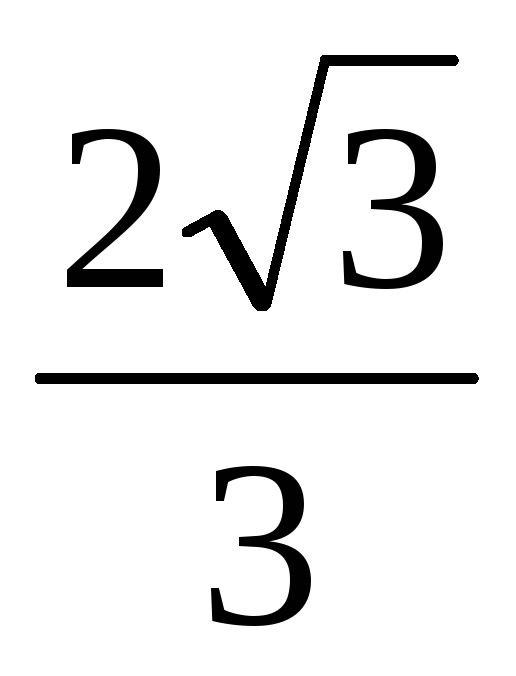. Найдите объем пирамиды.

30. В правильной треугольной пирамиде сторона основания равна 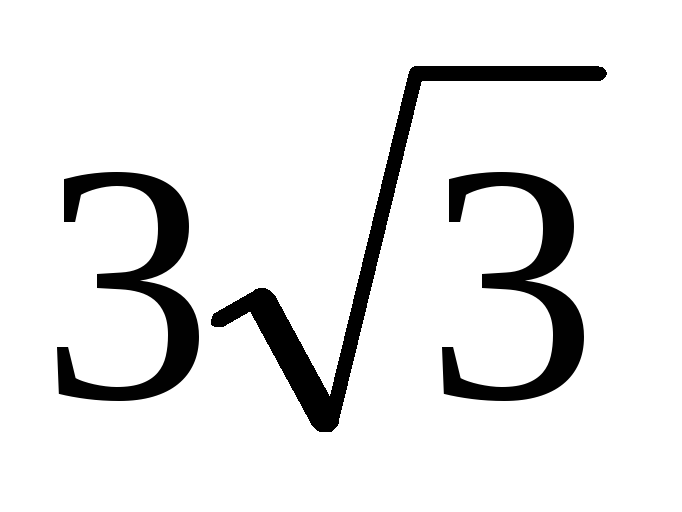. Через вершину основания проведено сечение, параллельное противопо­ложной стороне основания и перпендикулярное противоположной боко­вой грани пирамиды. Сечение наклонено к плоскости основания пирамиды под углом, тангенс которого равен 3/8. Найдите длину бокового ребра пирамиды.

31. В правильной пирамиде SABC сторона основания АВ = 3, боковое ребро SB = 6. Точка К лежит на ребре SB так, что SК : KB = 2 : 1. О — точка пересечения медиан грани SAB. Найдите площадь сечения, проходящего через точки С, К и О.

32. Высота правильной четырёхугольной пирамиды SABCD с основа­нием ABCD равна 8. Найдите сторону основания, если его центр удалён от боковой грани пирамиды на расстояние 4,8.

33. Высота правильной четырёхугольной пирамиды SABCD с основа­нием ABCD равна 4. Найдите сторону основания, если его центр удалён от бокового ребра пирамиды на расстояние 4/3.

34. Основанием пирамиды служит треугольник со сторонами 10, 13, 13. боковые грани пирамиды образуют с её основанием равные двугранные углы по 45°. Определите число, обратное значению объёма этой пирамиды.

35. Основанием пирамиды служит треугольник со сторонами 8, 10, 6. Бо­ковые рёбра наклонены к плоскости основания под углом 45°. Определите объём пирамиды.

36. В правильной четырёхугольной пирамиде расстояние от центра ос­нования до бокового ребра равно 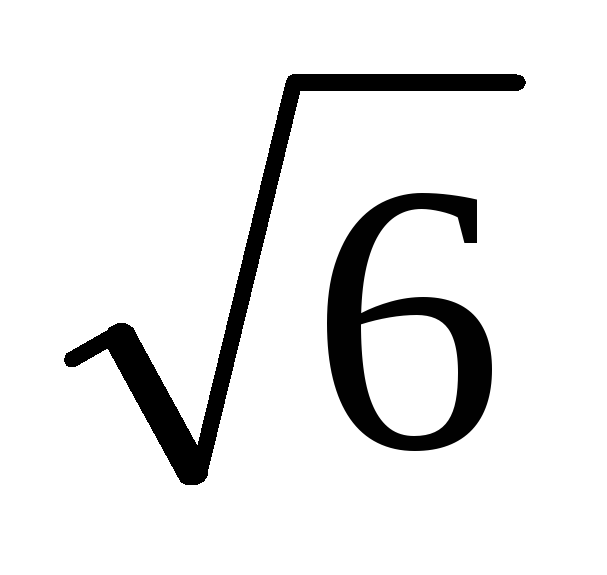, косинус угла между боковой гранью и основанием равен синусу этого угла. Найдите объём пирамиды.

37. В правильной треугольной пирамиде SABC сторона основания АВ = 4. Через прямую АВ проведено сечение, перпендикулярное боковому ребру SC и пересекающее его в точке К так, что SК : SC = 4 : 5. Найдите площадь боковой поверхности пирамиды.

38. В правильной четырёхугольной пирамиде SABCD с вершиной S сторона основания равна 3, а тангенс двугранного угла между боковой гранью и плоскостью основания равен 2. Найдите площадь боковой поверхности пирамиды SMNPQ, где М, N, P, Q — середины сторон осно­вания.

39. В пирамиде SABC основанием служит прямоугольный треугольник ABC с прямым углом В. В треугольнике ABC проведена биссектри­са ВК, причём оказалось, что SK — высота пирамиды. Известно, что АВ = 2, ВС = 4, SК = 1. Найдите расстояние от точки К до плоскости ABS.

40. Диаметр окружности, вписанной в основание правильной треугольной пирамиды, равен 10. Найдите объём пирамиды, если её боковые грани наклонены к плоскости основания под углом 30°.

41. Объём правильной треугольной пирамиды равен 27. Её боковые гра­ни наклонены к плоскости основания под углом 30°. Найдите диаметр окружности, вписанный в основание этой пирамиды.

42. Дана правильная треугольная пирамида SABC. Через ребро АС проведена плоскость, составляющая угол 60° с плоскостью основания и пересекающая прямую, содержащую высоту пирамиды, в точке К. Найдите объём пирамиды КABC, если ВС = .

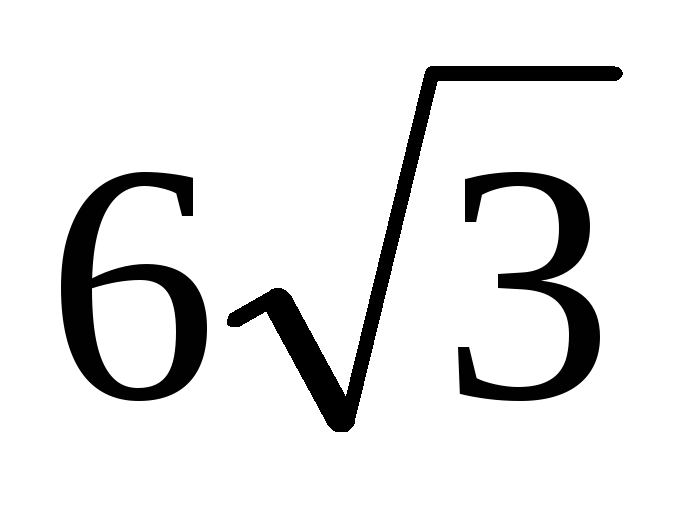43. Дана правильная четырёхугольная пирамида SABCD. Через ребро ВС проведена плоскость, составляющая угол 30° с плоскостью основа­ния и пересекающая прямую, содержащую высоту пирамиды, в точке К. Найдите объём пирамиды KABCD, если АС = .

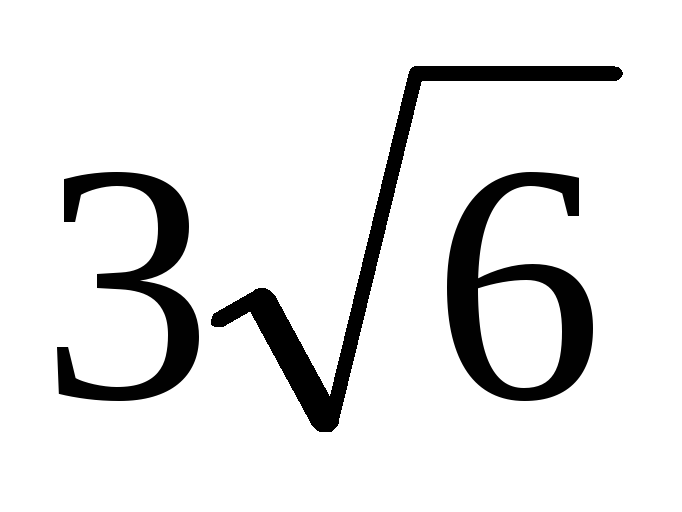44. Площадь основания правильной пятиугольной пирамиды равна 17, а все двугранные углы при основании равны 60°. Найдите площадь боковой поверхности пирамиды.

45. Полная площадь поверхности правильной четырёхугольной пирамиды равна 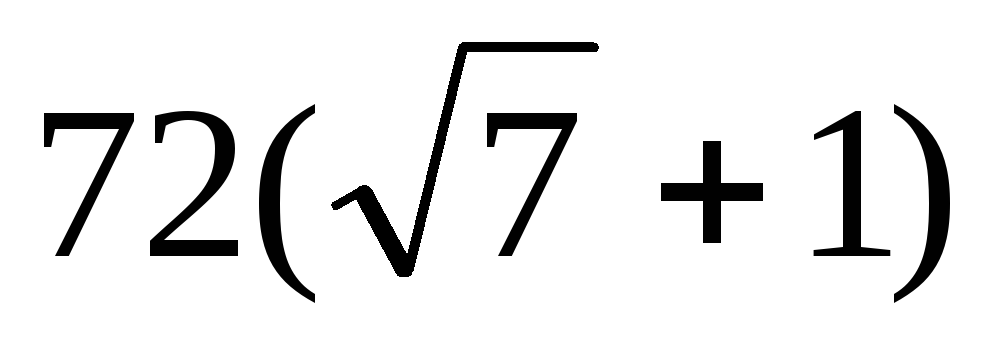, а плоский угол при её вершине, заключённый между противоположными рёбрами, равен 60°. Найдите радиус окружности, описанной около основания пирамиды.

Призма. Параллелепипед

46. Боковые рёбра призмы ABCA₁B₁C₁, в основании которой лежит равносторонний треугольник, наклонены к плоскости основания под уг­лом в 60°. Отрезок АС₁ перпендикулярен плоскости основания. Найди­те длину этого отрезка, если площадь боковой поверхности призмы равна .

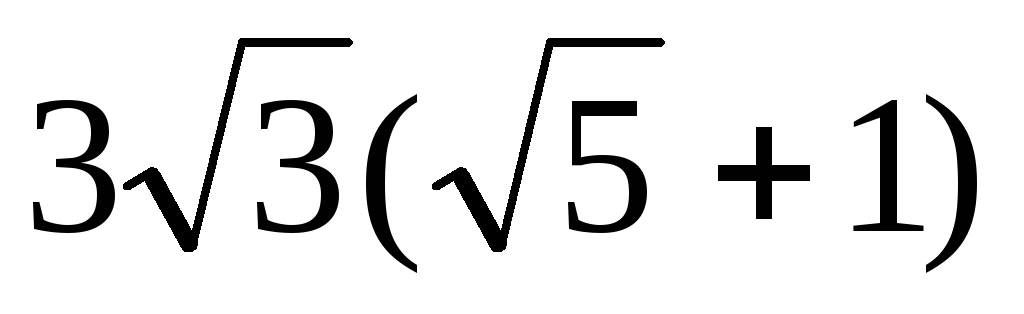47. Основанием наклонной призмы АВСА₁В₁С₁ с боковыми рёбра­ми АА₁, ВВ₁, СС₁ является правильный треугольник ABC со стороной 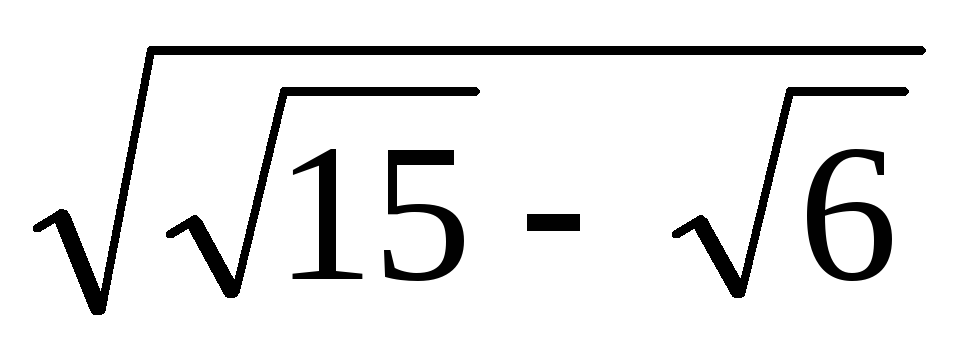. Вершина А₁ проектируется в центр грани ABC. Ребро АА₁ составляет с плоскостью основания угол 45°. Найдите площадь боковой поверхности призмы.

48. Дана прямая призма АВСА₁В₁С₁, в основании которой лежит пря­моугольный треугольник ABC с гипотенузой СВ=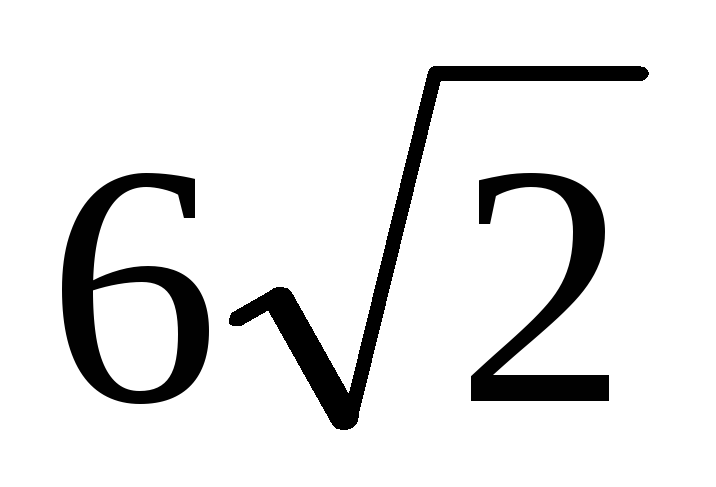. Угол меж­ду плоскостями CAB и АВС₁ равен 30°. Найдите угол между плоскостями ABC и А₁ВС, если ребро ВВ₁ = 4.

49. В основании прямой призмы лежит прямоугольный треугольник АВС. Катет ВС стягивает дугу, равную 60°. Через диагональ боковой грани, проходящей через другой катет АС, проведена плоскость, перпен­дикулярная этой грани и образующая с плоскостью основания угол 30°. Определите радиус описанной около треугольника ABC окружности, ес­ли площадь сечения равна 16.

50. Основанием прямой призмы ABCA₁B₁C₁ является равнобедренный треугольник ABC с основанием ВС=12, и боковой стороной АВ=15. Высота призмы равна 0,8. Плоскость α проходит через точку пе­ресечения медиан основания ABC и через середины рёбер А₁В₁ и В₁С₁. Найдите площадь сечения призмы плоскостью α.

51. Основанием прямой призмы АВСА₁В₁С₁ является прямоугольный треугольник ABC с прямым углом С. Высота призмы равна 2. Найдите расстояние от точки С₁ до прямой АВ, если расстояние от точки В₁ до прямой АС равно 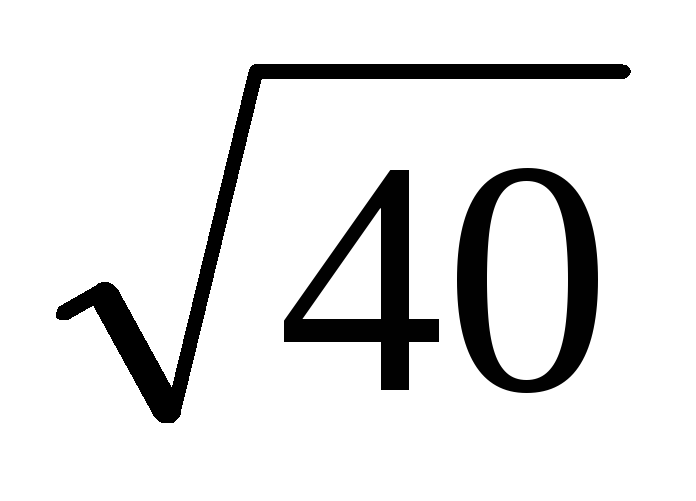, а расстояние от точки А₁ до прямой ВС равно .

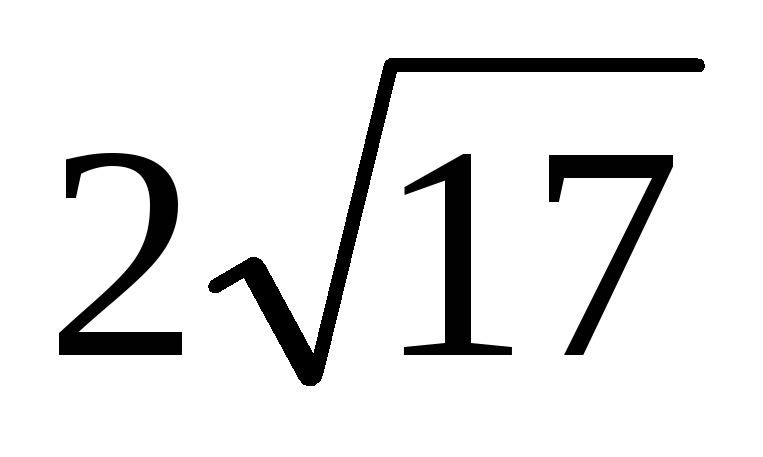52. Основание прямой призмы АВСА₁В₁С₁ — треугольник ABC, пло­щадь которого равна 6, ВС = 4. Найдите тангенс угла между плоскостями АВС и А₁ВС, если площадь треугольника А₁ВС равна.

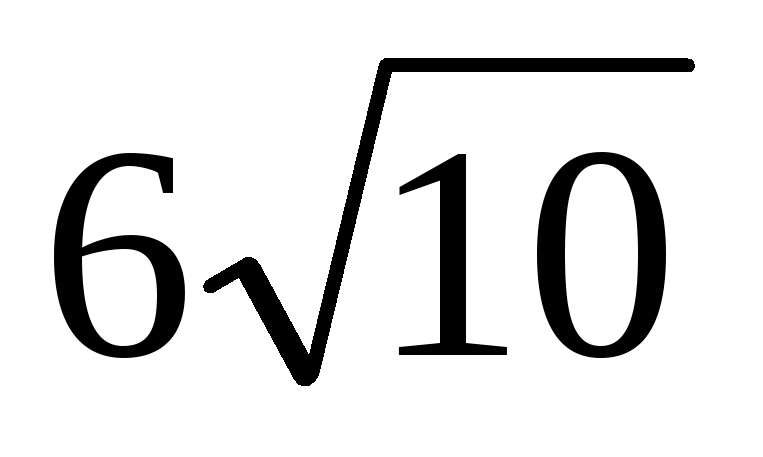53. Основание прямой призмы ABCDA₁B₁C₁D₁ — ромб ABCD со стороной, равной 7. Площадь ромба равна 28. Тангенс угла между плос­костью основания призмы и плоскостью АВС₁ равен 2,75. Найдите длину бокового ребра призмы.

54. Основанием прямой призмы ABCA₁B₁C₁ является прямоугольный треугольник с гипотенузой АВ и катетами АС = 3, ВС = 2. Высота приз­мы равна 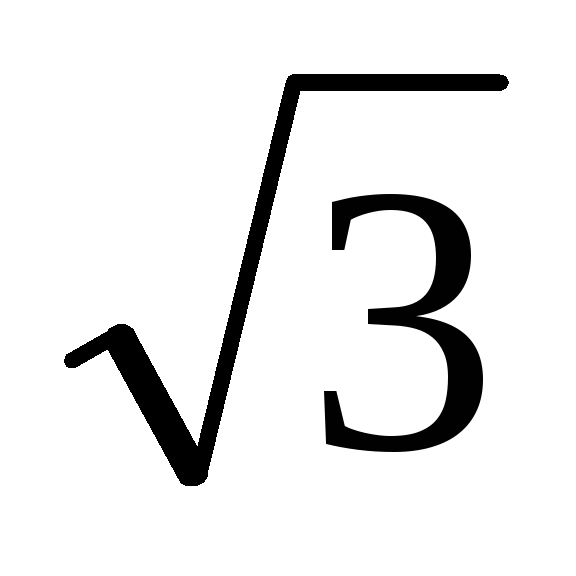. Найдите косинус угла между ребром АС и диагональю А₁В.

55. Основанием прямой призмы ABCA₁B₁С₁ является равнобедренный треугольник, в котором АВ = АС = 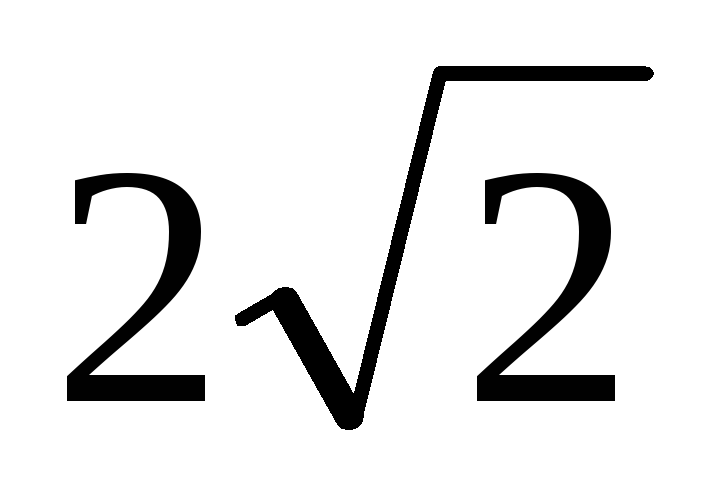, ВС = 2. Высота призмы рав­на 1. Найдите градусную меру угла между ребром АС и диагональю А₁В боковой грани.

56. В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁ высота равна 7, а диаметр описанной около боковой грани окружности равен 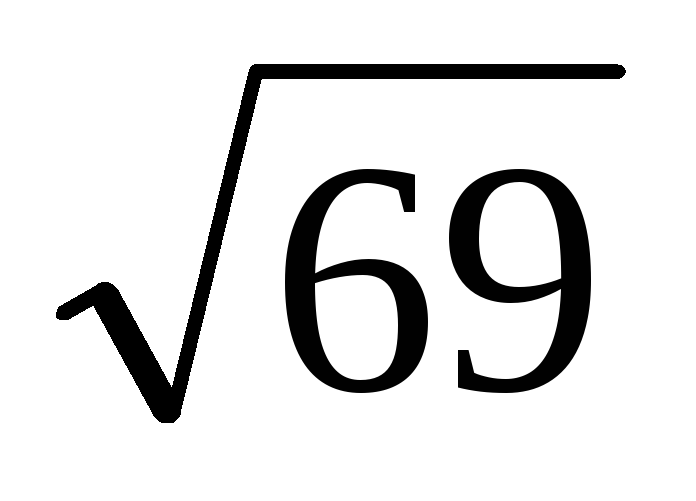. Найдите косинус угла между плоскостью А₁ВЕ и плоскостью AFF₁.

57. В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁ вы­сота равна 4, а диаметр описанной около основания окружности ра­вен 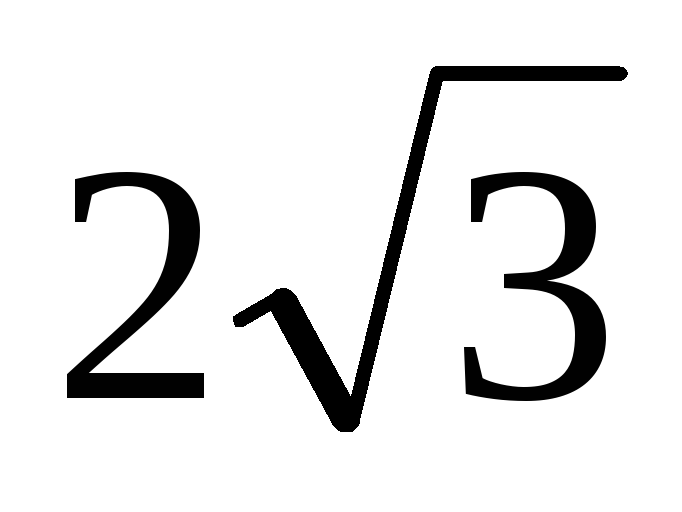. Найдите синус угла между плоскостью A₁CD и плоскостью ос­нования призмы.

58. В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁ вы­сота равна 5, а диаметр описанной около основания окружности равен 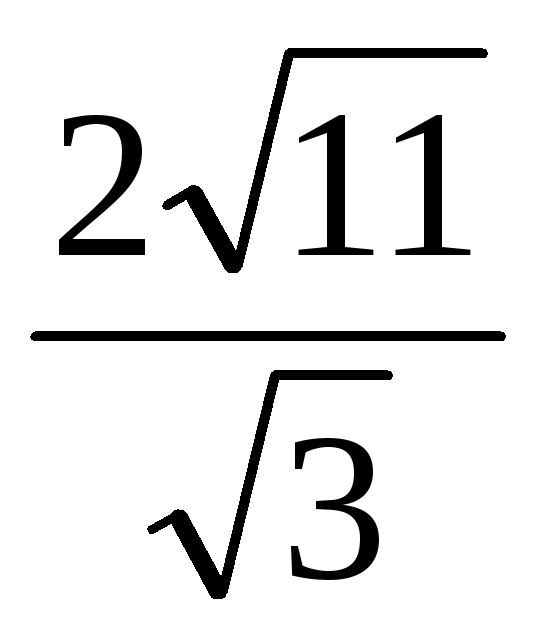. Найдите величину, обратную косинусу угла между плоскостями A₁CD и AF₁F.

59. Сторона ВС основания ABC прямой призмы ABCA₁B₁C₁ равна 20. Расстояние от точки B₁ до прямой АС равно 15, а синус угла между прямыми В₁С₁ и АС равен 0,6. Найдите высоту призмы ABCA₁B₁C₁.

60. Сторона ВС основания ABC прямой призмы ABCA₁B₁C₁ равна 15. Расстояние между прямыми В₁С₁ и АС равно 8, а синус угла между этими прямыми равен 0,4. Найдите расстояние от точки В₁ до прямой АС.

61. Высота прямой призмы ABCА₁В₁С₁ с основанием ABC равна 12. Угол между прямыми BC₁ и АС равен 90°, а синус угла между прямыми A₁B и АС равен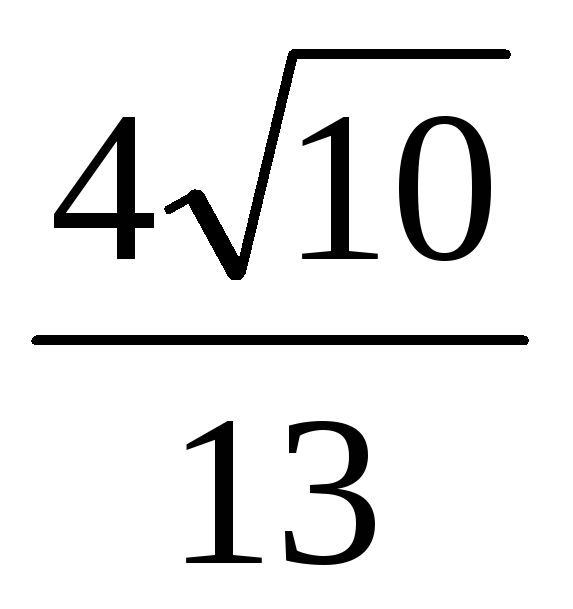. Найдите тангенс угла между плоскостью ВС₁А и АВС, если А₁В = 13.

62. Высота прямой призмы АВСА₁В₁С₁ с основанием АВС равна 3. Угол между прямыми ВС₁ и АС равен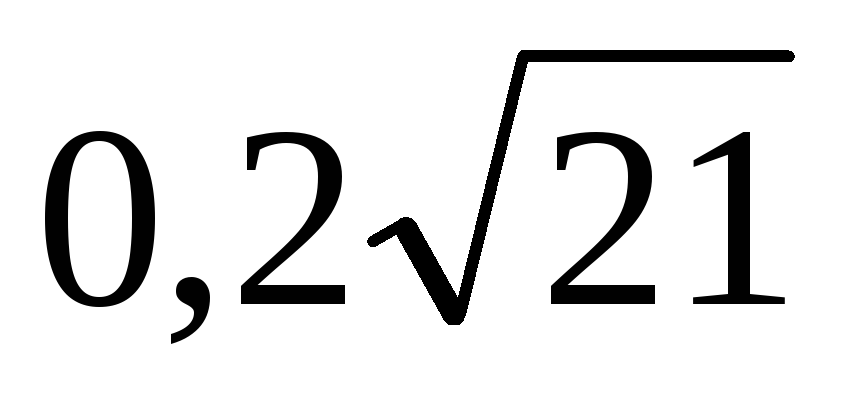. Найдите градусную меру угла между плоскостью АС₁В и прямой СС₁ если А₁В = 5.

63. В основании треугольной прямой призмы АВСА₁В₁С₁ лежит рав­нобедренный прямоугольный треугольник АВС, АВ = ВС. Через сто­рону АС проведена плоскость, пересекающая боковое ребро В₁В в точ­ке О и делящая его в отношении 1 : 3, считая от точки В₁. АС = 10. Высота призмы равна 16. Найдите отношение площадей треугольников S_ОАС : S_ABC.

64. В треугольной прямой призме АВСА₁В₁С₁ через сторону АС ниж­него основания проведена плоскость, пересекающая боковое ребро В₁В к точке О и делящая его в отношении 1 : 3, считая от вершины В₁ , ОК — высота треугольника АОС. Треугольник ОКВ — равнобедренный. Найдите отношение квадратов площадей треугольников АОС и АВ₁С.

65. Пусть ABCDА₁В₁С₁D₁ — прямоугольный параллелепипед. Диагонали смежных боковых граней АВ₁ и CB₁ составляют с АС углы α и β. Сколько градусов составляет угол между плоскостью АВ₁С и плос­костью основания, если tg α= 1, tg β = 4.

66. Пусть ABCDА₁В₁С₁D₁ —прямоугольный параллелепипед. Диагонали смежных боковых граней CB₁ и CD₁ составляют с B₁D₁ углы α и β. Сколько градусов составляет угол между плоскостью B₁CD₁ и плоскостью основания, если tg α = 0,5. tg β = 4.

67. В прямоугольном параллелепипеде АВСА₁В₁С₁ АВ = 2 и ВС = 4. На ребре АА₁ выбрана точка К так, что А₁К = 4, а на ребре ВВ₁ — точка L так, что B₁L = 3. Найдите площадь сечения, проходящего через точки K, L и D₁.

68. Высота прямой треугольной призмы АВСА₁В₁С₁ равна 10. Рассто­яние от вершины А до плоскости А₁ВС равно 6. Найдите площадь сечения призмы плоскостью A₁BC, если ВС = 16.

69. Высота прямой треугольной призмы АВСА₁В₁С₁ равна 12. Угол между плоскостью основания АВС и плоскостью А₁ВС равен α. Найдите расстояние от вершины А до плоскости А₁ВС, если известно, что sinα = 0,6.

70. В правильной треугольной призме площадь полной поверхности равна 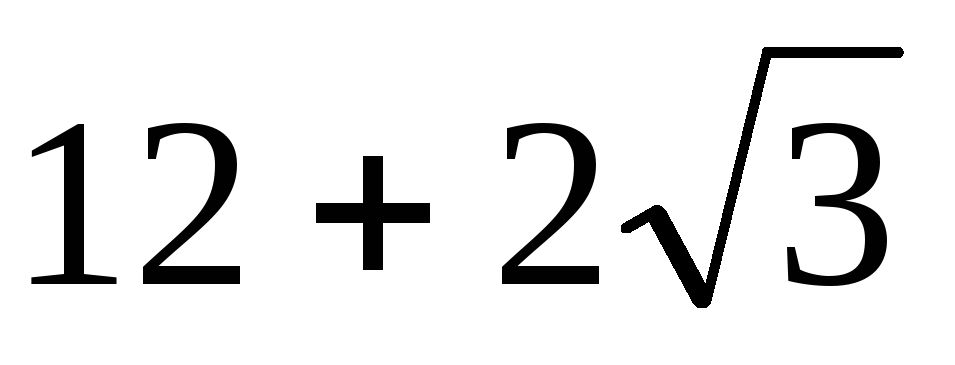. Найдите радиус окружности, вписанной в боковую грань призмы.

71. Найдите объём прямой треугольной призмы АВС А₁В₁С₁, у которой О — точка пересечения медиан треугольника ABC, C₁OC =45°, АС = ВС = 10, АВ = 12.

72. Высота прямой призмы ABCА₁В₁С₁ равна 12. Основание призмы — треугольник ABC, в котором АВ = АС, ВС = 18, tg C = 0,4. Найдите тангенс угла между прямой АС₁ и плоскостью ВB₁С₁.

73. Дана правильная четырёхугольная призма ABCDА₁В₁С₁D₁. Расстояние от точки С до плоскости BC₁D равно 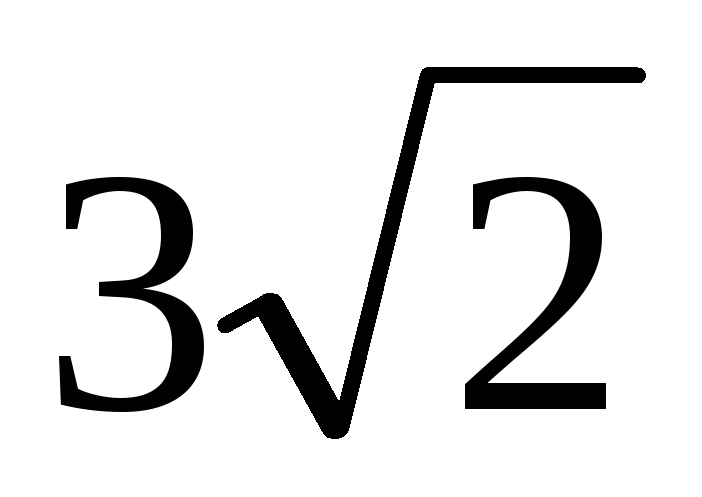. Плоскость ВС1D на­клонена к плоскости основания под углом 30°. Найдите сторону основа­ния призмы.

74. Дана правильная четырёхугольная призма ABCDА₁В₁С₁D₁. Расстояние от точки С до плоскости C₁DB равно 4. Плоскость C₁DB образует с плоскостью основания угол 45°. Найдите отношение объёма приз­мы к площади боковой поверхности.

75. Основание прямой призмы ABCDА₁В₁С₁D₁ — параллелограмм ABCD, в котором CD = 10, BAD = 30°. Высота призмы равна 15. Найдите тангенс угла между плоскостью основания призмы и плоскостью D₁BC.

76. Основанием прямой призмы ABCА₁В₁С₁ является равнобедренный треугольник ABC с прямым углом С. На рёбрах АА₁ и ВВ₁ взяты точки К и F соответственно так, что АК = ВF и АК : КА₁ = 1 : 2 . Найдите 3S_FКС если объём призмы равен 8, АС = .

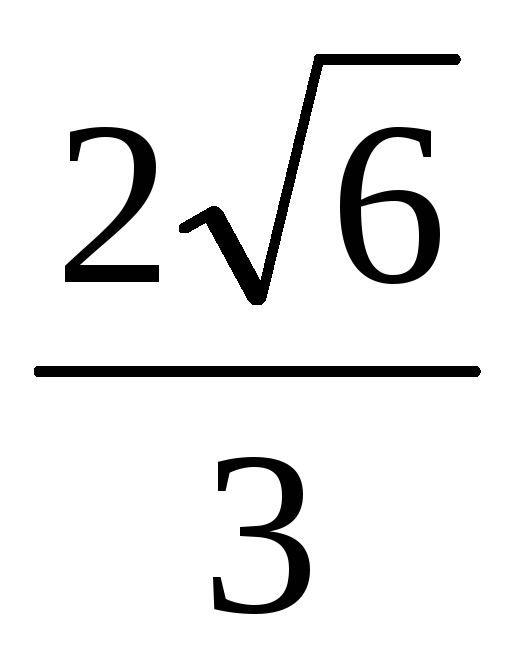77. Основанием прямой призмы АВСА₁В₁С₁ является прямоугольный треугольник ABC с прямым углом С. Через ребро СС₁ проведено сечение CC₁D₁D, перпендикулярное к плоскости АА₁В. Найдите площадь сечения, если объём призмы равен 10,2. AD = 0,9. BD = 2,5.

Куб

78. В кубе ABCDА₁В₁С₁D₁ расстояние между вершиной А и серединой ребра D₁C₁ равно 3. Найдите площадь полной поверхности куба.

79. Точки А, В и С — середины попарно скрещивающихся рёбер куба. Найдите расстояние от точки А до прямой ВС, если ребро куба равно .

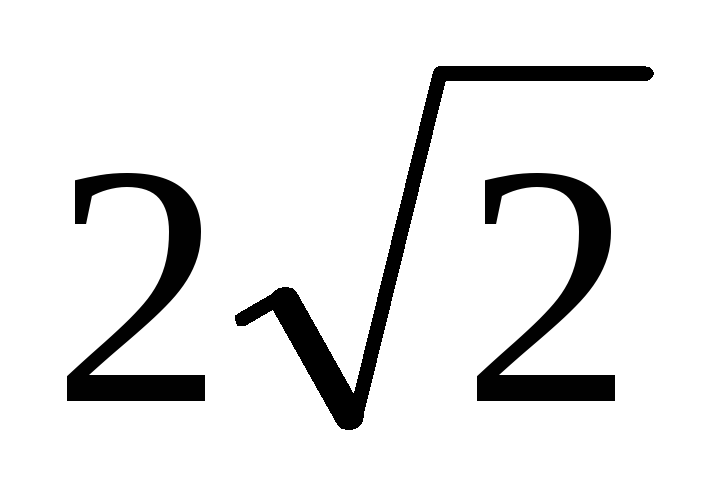80. Ребро куба ABCDА₁В₁С₁D₁ равно 6. Точка L — середина ребра АВ, точка N— середина ребра DD₁. Найдите объём пирамиды AA1LN.

81. Объём куба ABCDA₁B₁C₁D₁ равен 18. Точки L, К, М, N, L₁ , К₁ , M₁ , N₁ лежат соответственно на сторонах АВ, ВС, CD, DA, А₁В₁ , В₁С₁ , C₁D₁ , D₁A₁ . Найдите объём многогранника LKNМL₁K₁M₁N₁. Если .

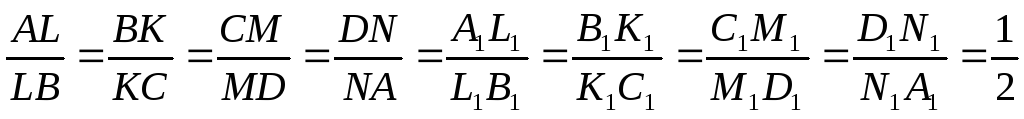Конус

82. Угол между образующими СА и СВ конуса равен 60°, высота конуса равна 7,5, а АВ=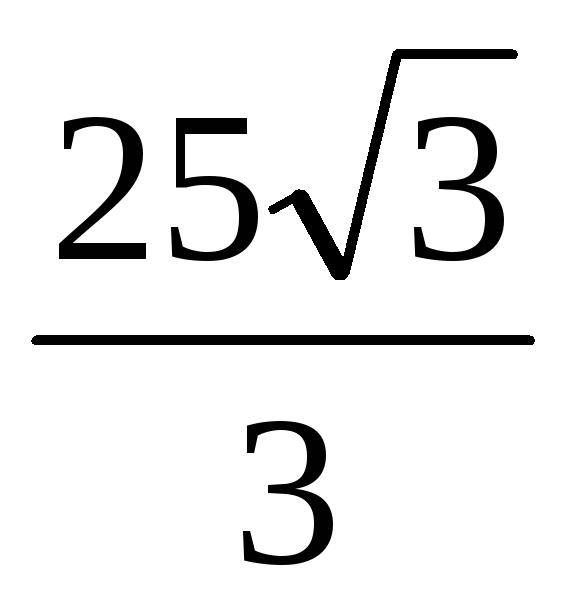. Найдите расстояние от центра основания конуса до плоскости ABC.

83. Высота прямого кругового конуса равна 15, а радиус его основания равен 25. Плоскость, проходящая через вершину конуса и удалённая от центра его основания на расстояние, равное 12, пересекает основание ко­нуса по отрезку АВ. Найдите длину отрезка АВ.

84. Радиус основания конуса равен 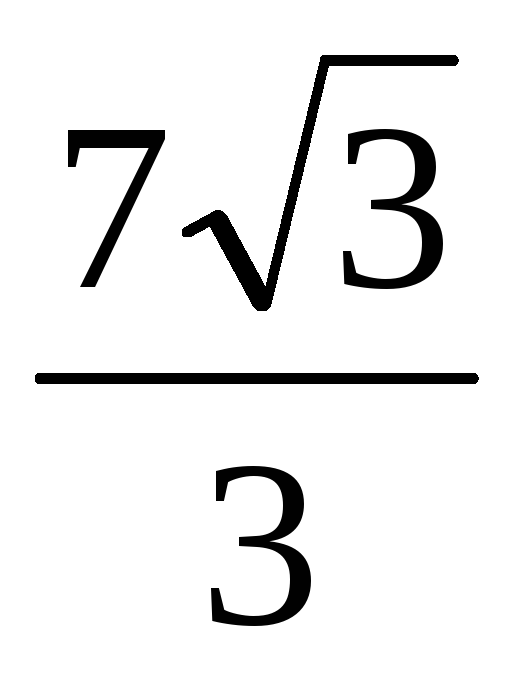, а его высота равна 7. Найдите расстояние между образующей конуса и перпендикулярной ей прямой, на которой лежит диаметр основания.

85. Радиус основания прямого кругового конуса равен 3, а площадь бо­ковой поверхности равна 15π. Найдите площадь осевого сечения этого ко­нуса.

86. Объём прямого кругового конуса равен 100π. Найдите отношение площади боковой поверхности конуса к площади его основания, если вы­сота конуса равна 12.

Цилиндр

87. Радиус основания цилиндра равен 6. Основание ВС равнобедрен­ного треугольника ABC является хордой окружности одного основания этого цилиндра, а вершина С лежит на окружности другого основания. Длина боковой стороны треугольника ABC равна 12, а его проекцией на основание цилиндра является правильный треугольник. Найдите площадь осевого сечения цилиндра.

88. Высота цилиндра равна 80, а радиус основания — 26. В окружность основания вписан остроугольный треугольник ABC такой, что ВС = 20, и АВ = АС. Отрезки АА₁ и ВВ₁ — образующие цилиндра. Найдите ко­тангенс угла между плоскостью СВВ₁ и плоскостью ВА₁С.

89. Высота цилиндра равна 40, а радиус основания 26. В окружность ос­нования вписан тупоугольный треугольник ABC такой, что ВС = 20, АВ = АС. Отрезки АА₁ и ВВ₁ — образующие цилиндра. Найдите тан­генс угла между плоскостью СВВ₁ и плоскостью ВА₁С.

90. Радиус основания цилиндра равен 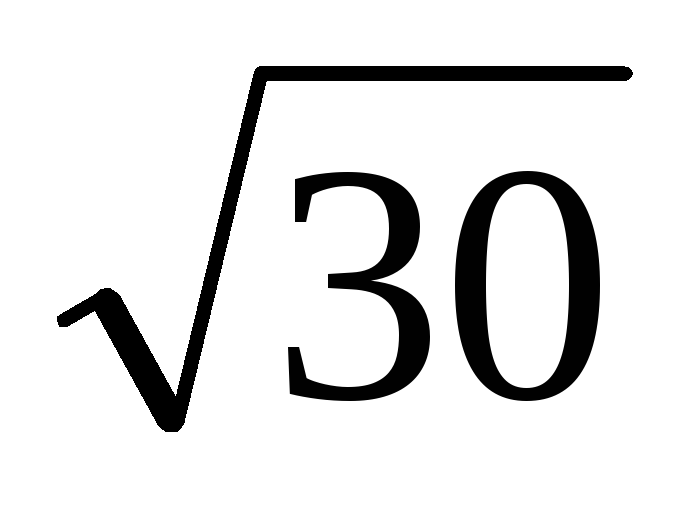, а высота равна 6. Отрезки АВ и CD — диаметры одного из оснований цилиндра, а отрезок АА₁ его образующая. Известно, что sinBCD =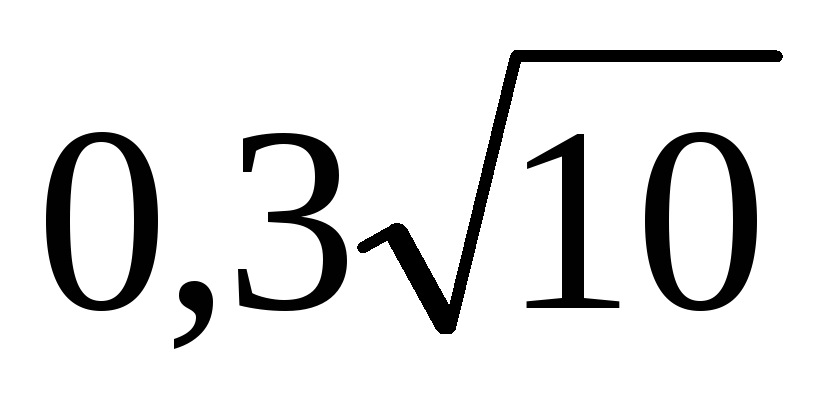 Найдите градусную меру.