1.4. Законы распределения носителей в зонах полупроводника

В теории твердого тела показывается, что энергетические уровни распределены по высоте разрешенной зоны неравномерно: плотность их меняется от границы в глубь зоны. Таким образом, каждому уровню с энергией соответствует определенная плотность , т. е. число уровней, отнесенное к единице энергии и единице объема твердого тела. Вблизи «дна» и «потолка» каждой из разрешенных зон плотность уровней (1/Дж см³) для узких интервалов энергии выражается следующей формулой:

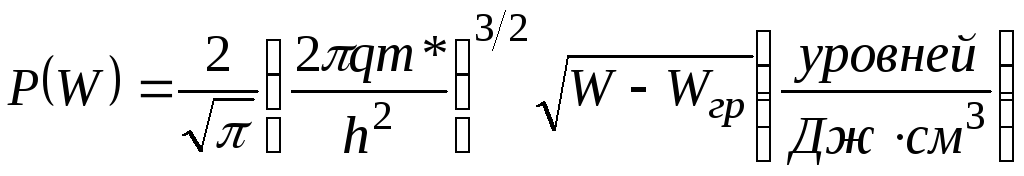(1-1,а)

Здесь h – постоянная Планка (); m* - эффективная масса; энергия отсчитывается от граничного уровня внутрь зоны.

Вероятность нахождения электрона на том или ином уровне дается распределением Ферми - Дирака

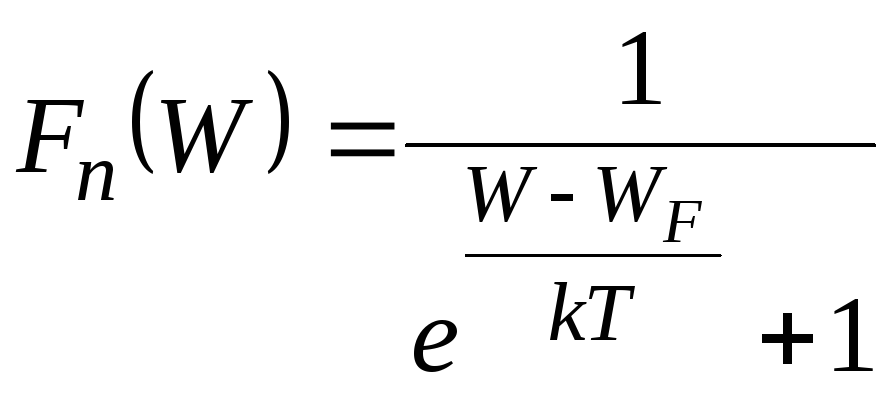, (1-1,б)

где k – постоянная Больцмана (); T – абсолютная температура; - энергия, называемая уровнем Ферми (энергия соответствует энергетическому уровню, вероятность заполнения которого равна 1/2).

В дальнейшем будет удобнее выражать энергию не в джоулях, а в электрон-вольтах или просто в вольтах. Чтобы перейти от одной размерности к другой, достаточно разделить энергии и на элементарный заряд электрона . Сделав такую замену в формулах (1-1), получим

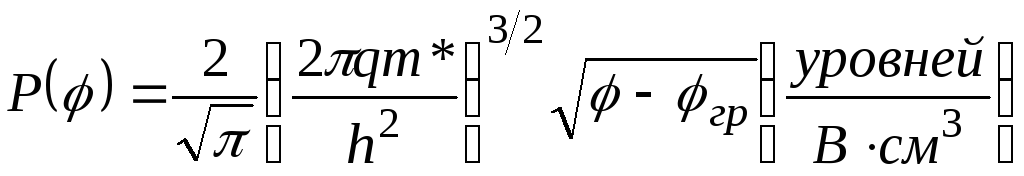; (1-2,а)

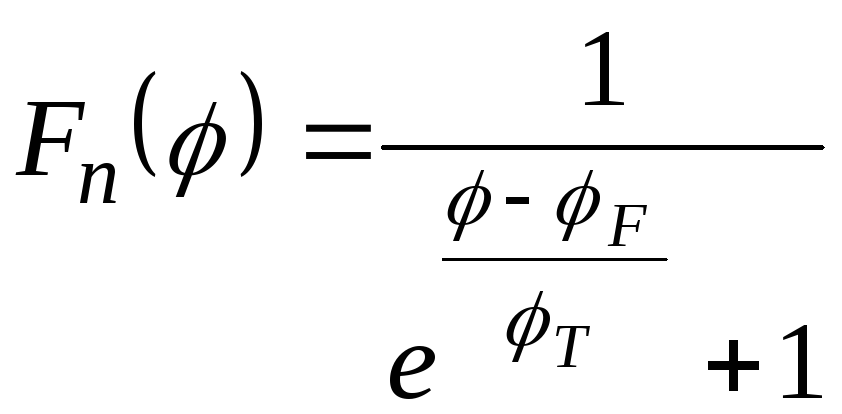, (1-2,б)

где - потенциал, характеризующий энергию; - уровень Ферми (потенциал Ферми в вольтах); - температурный потенциал:

. (1-3)

Н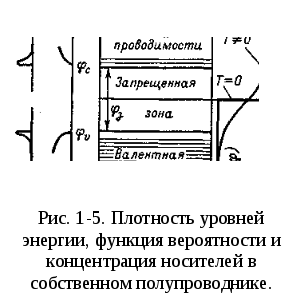азвание «температурный потенциал» для величины вполне оправдано, поскольку она имеет размерность напряжения и пропорциональна температуре. С физической точки зрения температурный потенциал есть выраженная в электрических единицах статистическая температура или близкая к ней средняя кинетическая энергия свободного электрона в электрическом газе. Полезно запомнить, что при температуре (которую мы условно будем называть «комнатной» температурой ) температурный потенциал равен .

В невырожденных полупроводниках уровень Ферми всегда лежит в запрещенной зоне. Глубину его залегания можно характеризовать «расстоянием» от одной из разрешенных зон, выраженным в единицах температурного потенциала. В большинстве случаев уровень Ферми залегает глубоко, т. е. соблюдаются неравенства

; (1-4,а)

, (1-4,б)

где и - потенциалы «дна» зоны проводимости и «потолка» валентной зоны.

При температуре функция имеет ступенчатый характер, это соответствует уже известным фактам: валентная зона полностью заполнена , зона проводимости пуста .

При температуре ступенька функции сглаживается и получается конечная (хотя и крайне малая) вероятность нахождения электронов в зоне проводимости. Одновременно вероятность нахождения электронов в валентной зоне делается немного меньше единицы. В последнем случае удобнее пользоваться вероятностью отсутствия электронов на уровнях или, что то же самое, вероятностью наличия дырок:

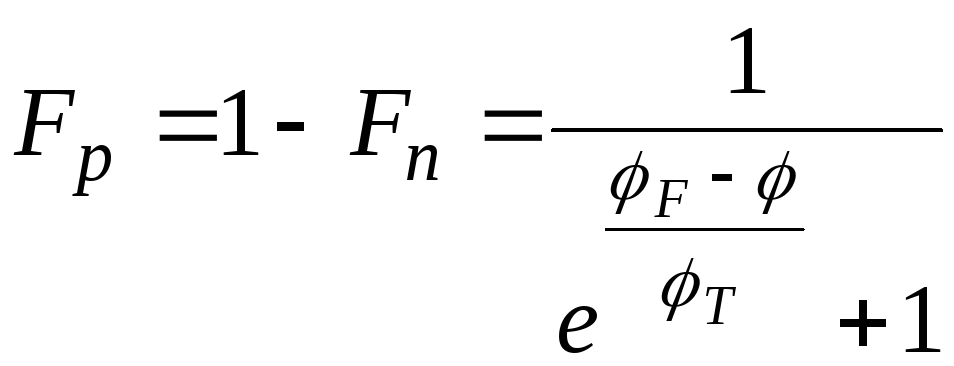, (1-5)

Учитывая неравенство (1-4а), нетрудно убедиться, что в зоне проводимости, где , экспонента в выражении (1-2б) намного превышает единицу и функция упрощается:

. (1-6,a)

Аналогично, учитывая неравенство (1-4б), нетрудно убедиться, что и в валентной зоне, где , экспонента в выражении (1-5) намного превышает единицу и функция упрощается:

. (1-6,б)

Функции (1-6), которые являются частным случаем распределения Ферми – Дирака (для области энергий, достаточно отличных от энергии ), называются распределением Максвелла – Больцмана. Это распределение представляет собой основу теории полупроводников.

Концентрация свободных электронов в зоне проводимости определяется интегралом

,

где подынтегральное выражение есть количество заполненных уровней в элементарном интервале энергий , расположенном в зоне проводимости, а множитель 2 означает, что на каждом уровне могут (по принципу Паули) находиться два электрона.

Подставив (1-2а) и (1-6a) под знак интеграла, после преобразований получим:

(1-7,a)

где - эффективная плотность состояний в зоне проводимости; - эффективная масса электрона; m – масса свободного электрона.

Концентрация свободных дырок в валентной зоне определяется интегралом

.

Подставив сюда (1-2.а) и (1-6.б), после преобразований получим:

, (1-7,б)

где - эффективная плотность состояний в валентной зоне.

Из выражений (1-7) следует, что

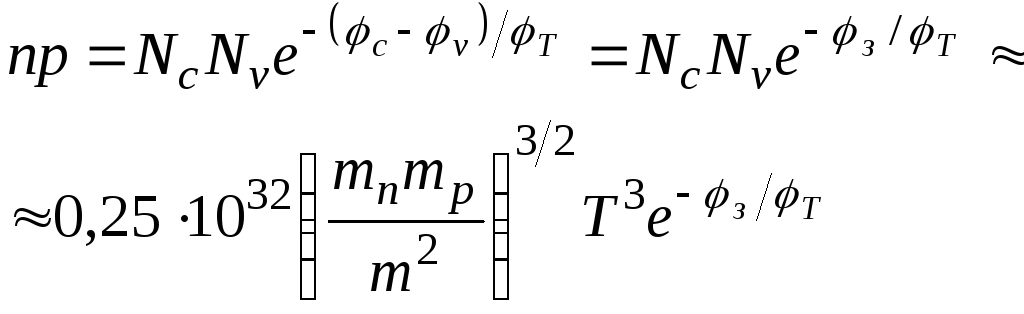(1-8)

где - ширина запрещенной зоны.

Ширина запрещенной зоны – один из важнейших параметров полупроводников: он определяет энергию, необходимую для образования электронно-дырочных пар. Ширина запрещенной зоны зависит от температуры: , где - ширина запрещенной зоны при ; - температурная чувствительность. Для кремния , , отсюда при комнатной температуре.

Так как при определенной температуре все члены, входящие в уравнение (1-8), постоянны то

.

Таким образом, следует важный вывод.

В равновесном состоянии произведение концентраций носителей зарядов для данного полупроводника при определенной температуре есть величина постоянная, не зависящая от концентрации и распределения примесей.

Из формул (1-7) легко получить отношение концентраций в следующем виде:

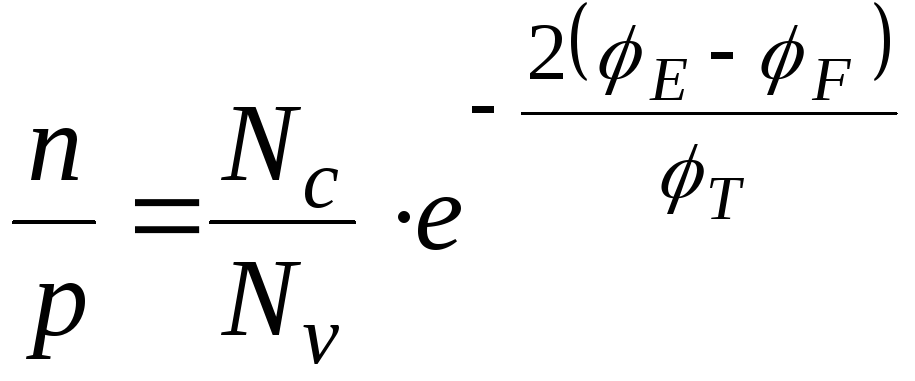(1-9)

где - потенциал середины запрещенной зоны, который называют также электростатическим потенциалом полупроводника.