Алгоритмы операций

Порядок выполнения команд в процессоре можно представить в следующем виде:

1. выборка команды из памяти и определение адреса следующей команды;

2. декодирование команды;

3. вычисление адреса операндов;

4. считывание операндов;

5. собственно выполнение команды и формирование признака результата;

6. запись результата.

В данном курсовом проекте считаем, что п.1-3 уже выполнены и адреса операндов уже известны.

1. Алгоритм операции FSubRP ST(i), ST.

Исходя из изложенного выше укрупненный алгоритм операции FSubRP ST(i), ST представим на рис.9. Соответственно разработка алгоритма состоит из 5 этапов.

Рис. 9. Укрупненный алгоритм операции FSubRP ST(i), ST

1. Первый этап. Чтение операндов в БОД.

Операнды читаются из вершины стека в рабочий регистр RG1: RG1=ST(i), RG2: RG2=ST. Разность формируется в RG3. Регистр операндов RG1 и RG2, и регистр разности RG3 подразделяются на субрегистры знаков: (S1,S2,S3), порядков (E1,E2,E3) и мантисс (M1,M2,M3). Регистры мантисс расширены до 68 бит для увеличения точности вычислений. Окончательный результат округляется до 32 бит.

2. Второй этап. Уравнивание порядков.

Прежде чем сделать операцию вычитания мантисс, необходимо уравнять порядки. Для этого вначале находим ∆Е = E1 – E2. Если ∆Е > 0, то производится сдвиг М2 на ∆Е вправо (dec ∆Е), если ∆Е < 0, то сдвигаем М1 на ∆Е вправо (inc ∆Е). Уравнивание заканчивается при ∆Е = 0. Если ∆Е > 67, то сразу обнуляем сдвигаемую мантиссу, чтобы исключить ненужные сдвиги. Порядок результата Е3 равен большему из Е1 и Е2. Алгоритм чтения операндов и уравнивания порядков приведен на рис. 10.

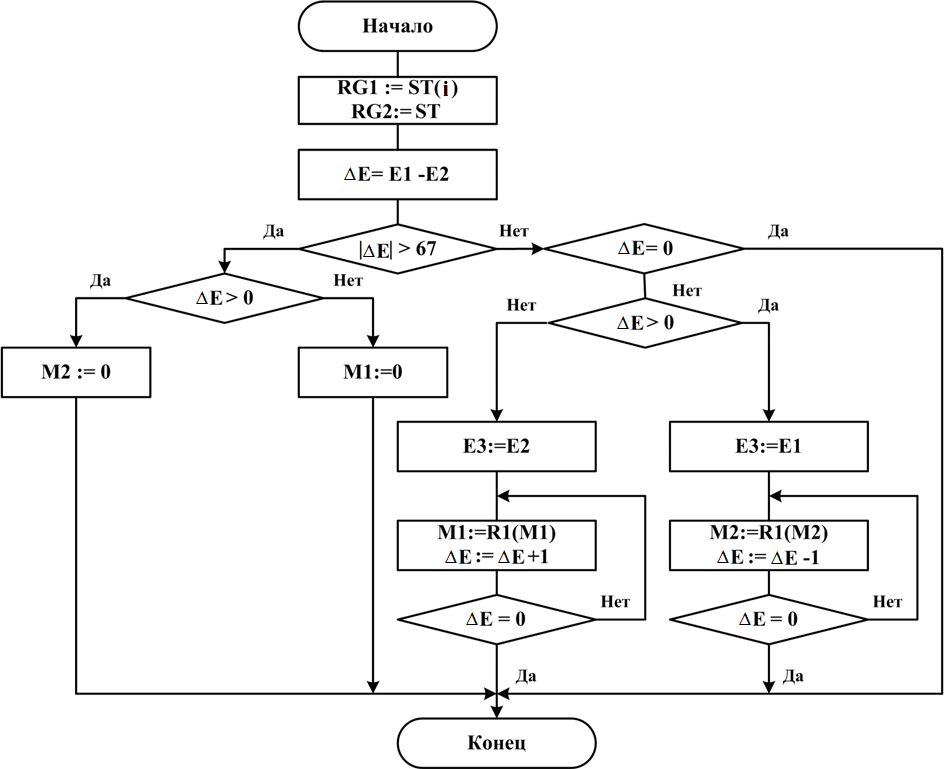
Рис. 10. Алгоритм чтения операндов и уравнивания порядков

3. Третий этап. Вычитание мантисс.

Обработка мантисс зависит от их знаков и происходит в соответствии с табл.1, где Sm – знак разности мантисс.

_{Обработка мантисс Таблица 1}

S1	S2	Действие над мантиссами	S3
0	0	M1-M2	Sm
0	1	M1+M2	0
1	0	M1+M2	1
1	1	M2-M1	Sm

В зависимости от знаков операндов (табл.1) производим сложение или вычитание мантисс. Алгоритм вычитания мантисс приведен на рис. 11.

Рис. 11. Алгоритм вычитания мантисс

4. Четвертый этап. Формирование результата.

Операция обратного вычитания FsubRP завершается нормализацией и округлением результата:

• если М3 получился в ДК, то М3 преобразуется в прямой код (ПК) M3 = not M3 + 1;

• если произошло переполнение мантиссы, то делаем нормализацию вправо: М3 = R1(M3), E3= E3 +1;

• если отсутствует явный бит в М3, то делаем нормализацию влево: М3 = Lk(M3), E3= E3 – k, где k – число ведущих нулей;

• округление М3 до 32 бит в зависимости от режима округления – поле RC (табл. 2), r – двоичный код в отбрасываемых битах мантиссы.

Округление результата _{Таблица 2}

RC	Режим	Действие округления
00	К ближайшему	Если r < 1000, то отбросить младшие биты. Если старший отбрасываемый бит 1 (r >=1000), то прибавить 1 к младшему сохраняемому биту.
10	Вверх
01	Вниз	При любом значении r отбрасываются младшие биты
11	Усечение

При нормализации возможны следующие особые случаи:

• мантисса М3 = 0 (потеря значимости);

• при инкременте Е3 возникает переполнение порядка;

• при декременте Е3 возникает антипереполнение порядка.

При возникновении подобных случаев фиксируются следующие признаки результата:

Z – нулевой результат;

S – знак результата;

P – потеря точности;

O– переполнение порядка;

U – антипереполнение порядка.

Маскированные реакции на особые случаи:

Z – запись в ST истинного нуля;

O– запись кода бесконечности: E=11...1 и M=1.000..0

U – запись кода нуля или денормализованного значения.

Алгоритм формирования результата представлен на рис. 12.

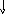
Рис. 12. Алгоритм формирования результата

5. Пятый этап. Запись результата в стек.

После нормализации и округления производится запись результата в стек, и извлечение из него: TOP ← TOP + 1.

Алгоритм записи результата представлен на рис. 13.

Начало

ST(I):=RG3

RG3:=TOP

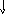
ТОР:=ТОР+1

Конец

Рис. 13. Алгоритм записи результата

2. Алгоритм операции FLd m32real.

Укрупненный алгоритм операции FLd m32real представим на рис. 14. Соответственно разработка алгоритма состоит из 3 этапов.

Рис. 14. Укрупненный алгоритм операции FLd m32real

1. Первый этап. Декремент поля TOP.

TOP ← TOP – 1.

2. Второй этап. Чтение операнда из ОП.

Адрес данного к началу операции уже вычислен и находится в адресном регистре EAR. По заданию длина слова ОП 64 бит. Поэтому операнд выбирается в регистр чтения RGR за один такт.

RGRW := MEM[EAR];

RGD[64; 0] := RGRW.

3. Третий этап. Запись операнда в вершину стека.

Перед загрузкой и декрементом TOP производится проверка тега регистра ST(7). Он должен быть пуст, так как этот регистр станет новой вершиной после декремента TOP, и его тег должен содержать код 11. В противном случае фиксируется переполнение. После чего происходит загрузка операнда в вершину стека. Алгоритм операции FLd m32real представлен на рис. 15.

Рис. 15. Алгоритм операции FLd m32real