Релятивистская механика

1. В направлении движения длина тела, движущегося со скоростью V относительно некоторой системы отсчета, связана с длиной тела, неподвижного в данной системе, соотношением

,

где c – скорость света.

2. Промежуток времени в системе, движущейся со скоростью V по отношению к наблюдателю, связан с промежутком времени в неподвижной для наблюдателя системе соотношением

.

3. Полная энергия тела массой m₀, движущегося со скоростью :

.

Если тело покоится (V = 0), то его энергия – это энергия покоя E₀:

.

4. Релятивистский импульс

.

5. Соотношение полной энергии, импульса и массы тела представляется выражением

.

Сочетание при любых скоростях тела остается неизменным, поскольку равно и называется инвариантом движения.

Легко запомнить связь между полной энергией, импульсом и энергией покоя с помощью прямоугольного треугольника (см. рисунок).

Рисунок к вопросу 5

По теореме Пифагора .

6. Релятивистская кинетическая энергия тела – это разность между полной энергией тела и его энергией покоя:

.

7. Связь между импульсом тела p, его массой m₀ и кинетической энергией задается соотношением

.

8. Преобразования Лоренца. Инерциальная система движется относительно инерциальной системы K вдоль оси Х со скоростью Переход от одной системы отсчета к другой позволяет производить следующие соотношения:

; ;

; ;

; ;

; ;

;

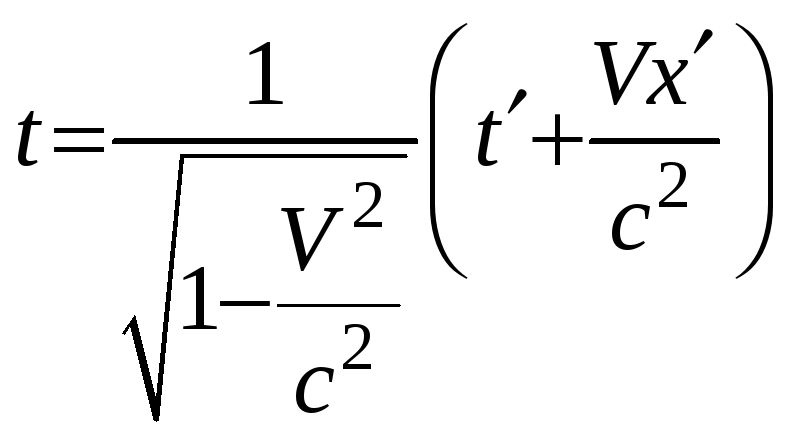
9. Интервал между событиями:

,

где – расстояние между точками пространства; – промежуток времени между событиями. Записанный в таком виде интервал инвариантен по отношению к преобразованиям от одной инерциальной системы к другой, т. е.

.

10. Изменение массы системы на соответствует изменению энергии системы

.

Молекулярная физика

1. Давление идеального газа

,

где – концентрация молекул; – средняя кинетическая энергия поступательного движения одной молекулы; – температура газа.

2. Средняя кинетическая энергия поступательного и вращательного движения одной молекулы

,

где i – число степеней свободы молекулы. Это число равно 3 для одноатомных молекул (три поступательных степени свободы), 5 – для двухатомных (три поступательных степени свободы и две вращательных) и 6 для трех- и многоатомных молекул (без учета колебаний молекул).

3. Барометрическая формула, выражающая зависимость давления идеального газа от высоты h над поверхностью Земли, есть

,

где – давление на высоте ; – молярная масса; – масса одной молекулы.

4. Распределение Больцмана (распределение концентрации молекул в силовом поле):

,

где – потенциальная энергия в точке пространства, где концентрация молекул газа равна .

5. Скорости молекул:

– средняя квадратичная;

– средняя арифметическая;

– наивероятнейшая.

6. Теплоемкость одного моля газа:

– при постоянном объеме;

– при постоянном давлении;

– показатель адиабаты.

Термодинамика

1. Внутренняя энергия идеального газа:

,

где – масса газа.

2. Первое начало термодинамики:

,

где – теплота, сообщенная газу; – изменение внутренней энергии газа; – работа, совершенная газом:

• при изохорическом процессе ()

, ;

;

• при изобарическом процессе ()

;

;

• при изотермическом процессе ()

,

, ;

• при адиабатическом процессе ()

,

.

3. Уравнение Пуассона. При адиабатическом процессе давление, объем и температура связаны следующими соотношениями:

.

4. Энтропия состояния равна , где W – термодинамическая вероятность состояния системы; k – постоянная Больцмана. Изменение энтропии системы при переходе из одного состояния в другое:

,

где 1 и 2 – пределы интегрирования, соответствующие начальному и конечному состояниям системы.