10.5.2. Зависимость спроса от дохода. Функции Торнквиста
В теории потребительского спроса
используются функции, моделирующие
связь между величиной дохода
потребителей и величиной их спроса
на различные товары (функции
Торнквиста). В зависимости от цены
на товары, эти функции имеют следующий
вид (рис. 10.3):
а) для малоценных товаров
;
б) для товаров первой необходимости
;
в
)
для товаров второй необходимости
(относительной роскоши)
;
г) для предметов роскоши
.
Величины
,
,
являются параметрами модели. Значение
показывает уровень насыщения спроса
малоценными товарами, товарами первой
или второй необходимости. Значение
показывает уровень дохода потребителей,
с которого начинается потребление
товаров второй необходимости и предметов
роскоши.
Теоретический материал: [1, гл. 5, 6], [2, гл. 4], [3, гл. 3, 3.6–3.9], [5], [8], [10], [12, гл. 3], [17], [19], [21], [27], [33, ч. 1, гл. 6], [40, т. 1, гл. 4].
Задания для решения на практическом занятии
1. Найти область определения функции:
а)
,
б)
,
в)
,
г)
.
2. Установить четность или нечетность функции:
а)
,
б)
,
в)
,
г)
.
3*. Найти наименьший положительный период функции:
а)
,
б)
.
4. С помощью преобразований построить график функции:
а)
,
б)
,
в)
,
г)
.
5. Показать, что функция
непрерывна в точке
двумя способами:
а)
,
;
б)
,
;
в)
,
.
6. Найти точки разрыва функции и указать их тип:
а)
,
б)
,
в)
,
г)
д)
.
7. Спрос и предложение на некоторый товар
на рынке описываются линейными
зависимостями вида
,
.
Определить равновесную цену. Установить
графическим способом, является ли
паутинная модель рынка «скручивающейся».
Заданы значения параметров
,
,
,
:
а)
;
б)
;
в)
;
г)
.
Задания для самостоятельной работы
1. Найти область определения функции:
а)
,
б)
,
в)
,
г)
.
2. Установить четность или нечетность функции:
а)
,
б)
,
в)
,
г)
.
3*. Найти наименьший положительный период функции:
а)
,
б)
.
4. С помощью преобразований построить график функции:
а)
,
б)
,
в)
,
г)
.
5. Показать, что функция непрерывна в
точке
двумя способами:
а)
,
;
б)
,
.
6. Найти точки разрыва функции и указать их тип:
а)
,
б)
,
в)
,
г)
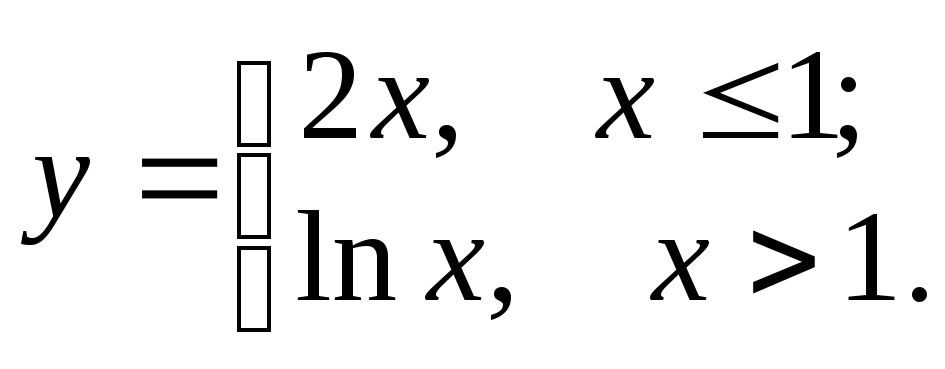
7. Спрос и предложение на некоторый товар
на рынке описываются линейными
зависимостями вида
,
.
Определить равновесную цену. Установить
графическим способом, является ли модель
паутинного рынка «скручивающейся»,
если заданы значения параметров
,
,
,
:
а)
;
б)
;
в)
;
г)
.
Тема 11. Производная и дифференциал. Производные высших порядков
11.1. Производная и дифференциал
Пусть функция
определена на множестве
,
,
,
точка
является предельной для множества
.
Определение 1. Производной
функции
в точке
называют предел отношения приращения
функции в этой точке к приращению
аргумента при 
(при условии, что этот предел
существует):
.
Определение 2. Функцию
называют дифференцируемой в точке
,
если ее приращение в этой точке можно
представить в виде
,
где
– вещественное число,
.
Теорема 1. Для того, чтобы функция
являлась дифференцируемой в точке
,
необходимо и достаточно, чтобы
.
Определение 3. Дифференциалом
функции
в точке
называют главную линейную относительно
часть приращения функции в этой точке:
.
Определение 4. Дифференциалом
независимой переменной называют
приращение
этой переменной:
.
Основные правила вычисления производных
1. Если функции
,
дифференцируемы в точке
,
то сумма (разность), произведение и
частное (при условии
)
этих функций также дифференцируемы в
точке
,
причем справедливы следующие формулы:
,
,
.
2. Если функция
дифференцируема в точке и
– число, то
.
3. Пусть функция
имеет производную в точке
,
а функция
имеет производную в точке
.
Тогда сложная функция
имеет производную в точке
и справедлива формула
.
4. Если функция
определена, непрерывна и строго монотонна
на отрезке
,
то у нее существует обратная функция
,
производная которой вычисляется по
формуле
.
Таблица производных основных элементарных функций
|
1.
|
2.
|
3.
|
|
4.
|
5. |
6. |
|
7.
|
8.
|
9.
|
|
10.
|
11.
|
12. |
|
13.
|
14.
|
15.
|
.
.
,
.
.
,
.
,
.
.
.
.
.
.
.
.
.
.Основные правила вычисления дифференциалов
1. Если функции
,
дифференцируемы в точке
,
принадлежащей их общей области
определения, то сумма (разность),
произведение и частное (при условии
)
этих функций также дифференцируемы в
этой точке, причем справедливы следующие
формулы:
,
,
.
2.
Если функция
дифференцируема
в точке
и
,
то
.
3. Пусть функция
дифференцируема в точке
,
а функция
дифференцируема в точке
.
Тогда сложная функция
дифференцируема в точке
и справедлива формула
.
Таблица дифференциалов элементарных функций
|
1.
|
2.
|
3.
|
|
4.
|
5.
|
6.
|
|
7.
|
8.
|
9.
|
|
10.
|
11.
|
12.
|
|
13.
|
14.
|
|
.
.
.
,
.
,
.
,
.
.
.
.
.
.
.
.
.
Пример 1. Вычислить производную
функции
.
Решение.
.
Пример 2. Найти первый дифференциал
функции
в точке
.
Решение. 1) Вычислим производную
функции
:
.
2) Вычислим значение производной функции
в точке
:
.
3) Тогда
.
Уравнение касательной к графику
функции
в точке
:
.
Определение 5. Нормалью к графику
функции
в точке
называют прямая, перпендикулярную к
касательной к графику функции
в точке
.
Уравнение нормали к графику функции
в точке
:
.
Геометрический смысл производной:
значение производной функции
в точке
равно тангенсу угла наклона к положительному
направлению оси
касательной к графику этой функции в
точке
.
Пример 3. Составить уравнения
касательной и нормали к графику функции
в точке
.
Решение. 1) Вычислим
при
:
.
2) Вычислим значение производной функции
в точке
:
.
3) Составим уравнение касательной:
или
.
4) Составим уравнение нормали:
или
.
Экономический смысл производной:
производная объема произведенной
продукции по времени
есть производительность труда в момент
.