Решение. В условиях этой задачи система (15.2) принимает

вид

3x² + 6у² - 2 = 0,

^Х + ^у₃ + ^Z = ^1, (15.3) x+3 У z ^{v 7}

X + 3 y 2'

Решение задачи сводится к исключению переменных X, y, z из этой системы. Находим выражения для X, у, 2 через x, y, z, используя два последних соотношения системы:

_ = (x + 3) - 3у - 3z ₂ = 4у _ = 4z

^X = (x + 3) + у + z ^,У = (x + 3)+ у + z^,Z = (x + 3)+ у + z'

Подставляем эти выражения в первое уравнение системы (15.3). Получаем

3[(x + 3) - 3у - 3z]² + 96у² - 4z[(x + 3)+ у + z] = 0 -

искомое уравнение конической поверхности. Как видим, это уравнение однородно относительно (x + 3), , z.

Ответ: 3[(x + 3) - 3у - 3z]² + 96у² - 4z[(x + 3) + у + z] = 0.

x — 2 у z 15.4. Прямая —3— =2=6 вращается вокруг оси OX.

Найдите уравнение описанной ею поверхности.

Решение. Точка прямой Mq(2;0;0) находится на оси OX. Поэтому все прямые, полученные при вращении данной пря­мой вокруг оси OX, проходят через точку Мо(2;0;0). Следо­вательно, это коническая поверхность с вершиной в точке Мо.

Косинус угла, который образует данная прямая с осью OX,

₃₃

равен cos a = = —. Так как все образующие

V3² + 2² + 6^{2 7}

23. m n p

24. 3

25. то — = = - или 49m² = 9(m² + n² + p²), откуда

26. V m² + n² + p^{2 7}

27. следует, что 40m² - 9n² - 9p² = 0. Поскольку m = (x - 2)t,

наклонены к оси OX под этим же углом,

n = yt, p = zt, где t принимает любые значения, то уравнение 40(x - 2)² - 9y² - 9z² = 0 является искомым.

Ответ: 40(x - 2)² - 9y² - 9z² = 0.

Поверхность, описываемую вращением некоторой плоской кривой L вокруг оси l, расположенной в этой же плоскости, называют поверхностью вращения. Для записи уравнения по­верхности вращения декартову систему координат выберем спе­циальным образом. Одну из координатных плоскостей совме­стим с плоскостью, в которой расположена кривая L, а одну из осей координат направим по оси вращения l. При таком вы­боре системы координат кривая L может быть задана тремя способами: либо f (x,y) = 0, либо tp(x,z) = 0, либо ip(y,z) = 0 в соответствующей координатной плоскости.

Ось вращения в каждом из трёх случаев можно выбрать двумя способами. В книге [6] Каплана приведено простое пра­вило записи уравнения поверхности вращения для всех шести возможных случаев: "Чтобы записать уравнение поверхности вращения, нужно в уравнении кривой L, заданном в одной из координатных плоскостей, переменную, соответствующую оси вращения, оставить без изменения, а вторую переменную заме­нить на корень квадратный из суммы квадратов двух других координат, взятым со знаком ±." Впрочем, это правило следу­ет из вида уравнения поверхности вращения, полученного в [5] на стр. 110.

15.5. Запишите уравнение поверхности вращения, получен-

_x² _y²

ной вращением гиперболы — 9 = 1: а) вокруг оси OX;

б) вокруг оси OY.

Решение: а) согласно сформулированному правилу, пере-

_x² _y²

менную x в уравнении — — = 1 оставляем без изменения, а

9 "

переменную y заменяем на ±\/y² + z². В результате получим x^{2 2} + z^{2 2} + z² x²

искомое уравнение = 1 или = — 1. Эта

4 9 9 4

поверхность называется двуполостным гиперболоидом враще­ния. Он получается вращением гиперболы вокруг её действи­тельной оси;

б) в этом случае переменную оставляем без изменения, а переменную x заменяем на ±\/x² + z². Получаем искомое урав-

_x² _{+ z}^{2 2}

нение 4 9 = 1. Эта поверхность называется однопо-

лостным гиперболоидом вращения. Он получается вращением гиперболы вокруг её мнимой оси.

Двуполостной гиперболоид вращения и однополостной ги­перболоид вращения - частные случаи поверхностей второго порядка.

² _{+ z}² _x² _x² _{+ z}^{2 2}

Ответ: а) = —1, б) = 1.

15.6. Запишите уравнение поверхности, полученной враще­нием параболы z = у² а) вокруг оси OZ; б) вокруг оси OY.

Решение: а) заменяя переменную у на ±л/x² + у², получаем искомое уравнение z = x² + ². Такая поверхность называется эллиптическим параболоидом вращения. Она также является частным случаем поверхностей второго порядка;

б) в этом случае переменную z надо заменить на ±\/x² + z². Получаем ±\/x² + z² = у² или x² + z² = у⁴. Поверхность, за­данная этим уравнением, не является поверхностью второго порядка.

Ответ: а) z = x² + ², б) x² + z² = ⁴.

Нетрудно записать, пользуясь указанным правилом, урав-

_x2 2

нения поверхностей вращения эллипса +—= = 1 вокруг его

a² b²

осей симметрии OX и OY. В результате получим поверхность, называемую эллипсоидом вращения, также являющуюся част­ным случаем поверхностей второго порядка.

Задачи для самостоятельного решения

Охарактеризовать поверхности, заданные в декарто­вой системе координат OXYZ следующими уравнениями:

а) y² + z² = 4; б) ^x- + ^ = 1;

_x2 _y2 ^{4 16}

в) ^x_r - ^У_г = 1; г) y² = 6z;

д) y² - xy = 0; е) x² - z² = 0;

ж) x² + y² = 0; з) x² + 8y² + 16 = 0;

и) x² + z² - 4z = 0; к) y² + z² = -4z.

Нарисуйте эти поверхности.

Найдите уравнение цилиндра, проектирующего ок­ружность

Г x² + (y - 2)² + (z - 1)² = 25,

x² + y² + z² = 16,

на плоскость OXY.

Ответ: x² + 5y² - 8y - 12 = 0.

Найдите уравнение цилиндрической поверхности, на-

_x² _{+ y}² _{= 25,}

правляющей которого служит окружность _{z = 0,} а образующая параллельна вектору 1(5; 3; 2). Ответ: (2x - 5z)² + (2y - 3z)² = 100.

Найдите уравнение цилиндрической поверхности, зная что она проходит через кривую

(x - 1)² + (y + 3)² + (z - 2)² = 25, x + y - z = 2, а её образующая параллельна оси OY.

Ответ: (x - 1)² + (z - x + 5)² + (z - 2)² = 25.

Найдите уравнение цилиндрической поверхности, зная что её образующие составляют равные углы с тремя осями координат и касаются сферы x² + y² + z² = 1.

Ответ: (2x — y — z)² + (2y — x — z)² + (2z — x — y)² = 9.

15.12. Запишите уравнение конической поверхности, вер­шина которой находится в начале координат, а направляющая

x² + У² + (z — 5)² = 9,

дана системой уравнений ^ ^ Ответ: 2x² + 2y² + z² = 1.

Найдите уравнение конической поверхности с вер-

( ^У- + ^z- = ₁

шиной в точке (4; 0; —3), и направляющей < 25 9 ^,

[ x = 0.

y² [3(x — 4)+4(z + 3)]² ,

Ответ: — + ^ '- i ^>А- = (x — 4)².

25 9

Запишите уравнение конической поверхности с вер-

{z² x² i у = 0.

Ответ: + ^{(У b 2} =0.

a² b² c²

Запишите уравнение круговой конической поверхно­сти, проходящей через все три координатные оси.

мер, окружность

I ^x + ^y + ^z — ^1. Ответ: xy + xz + yz = 0.

Запишите уравнение поверхности вращения, образо­ванной вращением кривой y = e^x а) вокруг оси OX; б) вокруг оси OY.

Ответ. y² + z² = e^2x; y = e±^x2+^z2.

Найдите уравнение поверхности вращения, образо­ванной вращением прямой x + y = 2 а) вокруг оси OX; б) вокруг оси OY.

Указание. В качестве направляющей можно взять, напри-x² + y² + z² = ,

Ответ: (x - 2)² - y² - z² = 0; (y - 2)² - x² - z² = 0. 15.18. Запишите уравнение поверхности вращения, образо­ванной вращением прямой | ^ вокруг оси OZ.

Ответ: x² + y² = 1.

16. Поверхности второго порядка

Предлагается изучить по пособию [5] подразделы 2.9, 1.3.11 и 1.6.6.

Поверхностью второго порядка называется поверхность, ко­торая в декартовой системе координат может быть задана урав­нением

anx² + а22У² + a33z² + 2an>xy + 2ai3xz + 2a23yz+ , 1) +2aoix + 2ao2y + 2ao3 z + aoo = 0. ^(.)

Первая группа из шести слагаемых

aiix² + a22y² + a33z² + 2ai2xy + 2ai3xz + 2a23yz (16.2)

образует квадратичную форму, а следующие три слагаемых

2aoix + 2ao2y + 2ao3z -

линейную форму.

Упрощение уравнения (16.1) проводится по той же схеме, что и для кривых второго порядка. Сначала приводим квадра­тичную форму к главным осям, для чего находим собственные числа Ai, А2, A3 её матрицы и ортонормированный базис, состо­ящий из собственных векторов этой матрицы. После перехода к новому базису уравнение (16.1) примет вид

Aixi + А2У² + A3z² + aoi xi + ao2yi + ao3zi + aoo = 0. (16.3)

Дальнейшее упрощение уравнения (16.3) осуществляется пу­тём преобразования параллельного переноса системы коорди­нат в новое начало. В результате уравнение (16.1) будет при­ведено к каноническому виду.

Всё сказанное проиллюстрируем примерами.

16.1. Относительно правой декартовой системы координат задана поверхность S своим уравнением

6x² - 2y² + 6z² + 4zx + 8x - 4y - 8z + 1 = 0.

Охарактеризуйте поверхность S, приведя её уравнение к кано­ническому виду.

Решение. Полную характеристику поверхности можно дать, приведя её уравнение к каноническому виду. Для этого нахо­дим главные оси квадратичной формы

B = 6x² - 2y² + 6z² + 4zx. Записываем матрицу этой квадратичной формы

6 0 2

0 -2 0 206

Из характеристического уравнения

6 - A 0 2

33. (-2 - А)(А² - 12А + 32) = 0.

0 -2 - А 0 2 0 6 - А

Находим собственные числа: A = 4, A2 = 8, A3 = -2. Далее на­ходим единичные собственные векторы, отвечающие этим соб­ственным числам. Для А! =4 получаем систему

Г 2xi + 2x3 = 0,

-6x2 = 0.

34. 11

35. ного вектора ix, 11 = ( —=; 0; —

36. 22

1

/2'"' 72,

Аналогично, полагая А = А2 =8, получаем систему

^Г -2x + 2x3 = 0, -10x2 = 0

для координат собственного вектора, отвечающего собствен­ному числу Л2 = 8. Видим, что вектор (а, 0, а) - собствен­ный. В качестве второго базисного вектора можно принять век­тор ji = ( 77=; 0; 7= J. Поскольку матрица B симметрична, а 22

собственные числа различны, то её собственные векторы по свойству симметрического линейного оператора взаимно орто­гональны.

Третий собственный вектор, отвечающий собственному чис­лу Л3 = —2, можно найти таким же способом, как и первые два. Но можно поступить проще, найдя орт вектора [ii, ji].

—j.

Мы получили ki = (0; —1;0). Переходим от ортонормирован-ного базиса O, i, j, k к новому ортонормированному базису O, ii, ji, ki. Ортогональная матрица перехода Q и её обратная матрица Q~^l = Q^T имеют вид

Новые координаты x\,y\,z\ и старые x, y, z связаны соотноше­ниями

В подробной записи эти соотношения имеют вид

xi + yi

-z

-xi + yi

В декартовой системе (O, x , y , z ) уравнение данной поверх­ности принимает вид

4x² + 8y² - 2z² + 8 • + 4zi - 8 •

+1=0

39. 16

4x² + 8y² - 2z² + ^ • xi + 4zi + 1 = 0.

2

Выделяя полные квадраты, находим

4 (xi + ² + 8y² - 2(zi - 1)² = -1 + 4 • 2 - 2 = 5.

Проведём преобразование параллельного переноса в новое на­чало O₂ по формулам

x2 = xi + \/2,

^y2 ^{= y , z}2 ^{= z - 1.}

В декартовой системе координат (O2, x2, y2, z2) уравнение по­верхности примет вид

^4x2^{2 + 8y}2^{2 - 2z}2^{2 = 5,}

где

x2

x - z + 2

x+z

^y2

L z2 = -У - 1.

Уравнение поверхности легко записать в каноническом виде

^x2 + ^{y2 z2} = 1

5/4 5/8 5/2 = '

Таким образом, поверхность является однополостным ги­перболоидом. Плоскости x₂ = x z + 2 = 0, y₂ = x + z = 0, z2 = —y — 1 = 0 являются её плоскостями симметрии. Эти плос­кости пересекаются в центре симметрии O₂ - в начале новой системы координат. Решая систему

x — z — 2 = 0, x + z = 0, У + 1 = 0,

находим x = 1, y = 1, z = 1, т.е. новое начало O₂ находится в точке ( 1; 1; 1).

Используя полученные данные, легко представить располо­жение гиперболоида относительно старой системы координат. Его ось симметрии параллельна вектору j, а центр симметрии находится в точке ( 1; 1; 1).

16.2. Приведите к каноническому виду уравнение поверх­ности 2x² + 2y² + 3z² + 4xy + 2zx + 2yz — 8x + 12y — 4z + 3 = 0. Охарактеризуйте эту поверхность. Укажите соответствующие формулы преобразования координат.

Решение. Поступаем также, как и при решении задачи 16.1. Для квадратичной формы

B = 2x² + 2y² + 3z² + 4xy + 2zx + 2yz записываем матрицу

" 2 2 1

221 113

и находим её собственные числа и собственные векторы. Для этого решаем характеристическое уравнение

2- X 2 1

2- X

1

-X³ + 7X² - 10X = 0.

1 1 3 - X

Его корни X_i = 2, X₂ = 5, X₃ = 0.

Находим единичные собственные векторы. Для Xi =2 ко­ординаты собственного вектора (xi,x2,x3) удовлетворяют си­стеме

2x2 +x3 = 0, 2x_i +x₃ = 0,

x +x2 +x3 = 0,

40. 1 1 2 —j= ; =; —р I, т.е. орт

41. v/б х/6 у/в/

вектора ii можем взять вектор ii

вектора (а, а, -2а).

Аналогично, при X2 = 5, получаем систему

3x +2x2 +x3 = 0, 2x -3x2 +x3 = 0, x +x2 -2x3 = 0,

фундаментальная система решений которой также содержит одно решение вида (а, а, а). В качестве второго базисного век-

_{( )} • ( 1 1 1 ^

тора можно принять орт вектора (а, а, а), л = 1 = ; —= ; —= I.

333

В качестве третьего базисного вектора k_i примем орт век­тора

^[ii^{, j}i^]

1 . 1 .

⁷2^{i — 7}2^j

т.е. вектор ki

7=; ^;0) . Новый ортонормированный

22

базис i_i, j_i, k_i найден. Переходим от старого базиса i, j, k к но­вому. Матрицы перехода Q и её обратная матрица Q^-1 = Q^T имеют вид

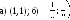
^Q

45. 0

^6

x + y + z x — У

⁷2 ^,

x + y 2z

49. ^y1 ^z1

x=

^y

z=

x1 + л/2у1 + \/3z1

x1 + \/2у1 — \/3z1 —2x1 + У2у1

⁷6 '

В декартовой системе координат (0,xi,yi,zi) уравнение дан­ной поверхности примет вид

xi + \/2yi + V3zi xi + \/2yi - \/3zi

8 • = + 12 • —

x/6 x/6

2x² + 5y² + 2\/6xi - 10\/2zi + 3 = 0. Выделяя полные квадраты, находим

²(xi + +5У²

1^\/2zi - 3 + 3 = 0.

Проведём преобразование параллельного переноса в новое на­чало O2 по формулам

x2 = x +

^y2 ^{= y , z}2 ^{= z .}

~2~^,

Получим