Завдання

1. Ознайомитись з будовою приладу ПМТ-3 та методикою вимірювань мікротвердості на ньому.

2. Користуючись методикою, викладеною в описі приладу ПМТ-3, нанести на поверхню досліджуваних зразків кремнію та виміряти значення діагоналей відбитків при навантаженнях P = 30 г. Час навантаження t = 10 c.

3. Провести вимірювання п.2 для запропонованих в роботі композиційних матеріалів при навантаженнях P = 100 г та часі навантаження t = 5-10 c.

4. За формулою (1.2) розрахувати мікротвердість досліджуваних матеріалів. Порівняти отримані значення з табличними даними.

5. Визначити похибку вимірювання мікротвердості за формулою:

. (1.3)

В розрахунках прийняти, що ∆Р ≈ 1 г. При навантаженнях 0.1 – 0.5 кг з високою точністю можна вважати, що ∆d ≈ 1 мкм.

Список літератури

1. Григорович В.К. «Твердость и микротвердость металлов». – М.: Наука, 1976. – 230 с.

Лабораторна робота № 4

Дослідження температурної залежності рухливості дислокацій та визначення енергії активації їхнього руху

Мета роботи: Вивчити особливості руху дислокацій в кремнії під дією температури, електричного струму та механічного навантаження на кристал.

Обладнання: мікротвердомір ПМТ-3, мікроскоп МИМ-8М, установка для деформації зразків.

Теоретичні відомості

У досконалому кристалі правильне періодичне розташування атомів (молекул, іонів) має місце у всьому об’ємі. В реальних кристалах спостерігається порушення правильного розташування атомів при збереженні цілісності кристалу. Ці порушення отримали назву дефектів. Розрізняють наступні типи дефектів:

1. Нульвимірні або точкові дефекти: вакансії, атоми занурення, домішкові атоми.

2. Одновимірні або лінійні дефекти – дислокації.

3. Двохвимірні або поверхневі дефекти: границі зерен та двійників, міжфазні границі, дефекти упаковки.

4. Тривимірні або об’ємні дефекти: порожнини, включення другої фази.

Наявність дефектів та їхня структура істотно впливають на фізичні властивості кристалів та їх механічні характеристики.

Найпростішими типами дислокацій є крайова та гвинтова. На рис. 3.1.а зображено схематичну будову ідеального кристалу у вигляді паралельних атомних площин. Якщо одна з цих площин обривається всередині кристалу (рис. 3.1.б), то місце обриву утворює крайову дислокацію. У випадку гвинтової дислокації характер зміщення атомних площин інший. Тут відсутній обрив всередині кристала якої-небудь атомної площини, але самі площини являють собою систему, подібну до гвинтових сходинок (рис. 3.1.в). Будь-яка дислокація може бути представлена у вигляді суми крайової та гвинтової дислокацій.

Рис. 3.1. Схематичне зображення атомних площин ідеального кристалу (а), та кристалу з крайовою (б) і гвинтовою (в) дислокаціями.

Відомо [1], що рух дислокацій в початково бездислокаційних кристалах вимагає подолання силових бар’єрів двох типів, які істотно різняться між собою. Перший тип регулярних лінійних бар’єрів пов'язаний з існуванням періодичного силового поля кристалічної решітки – це рельєф Пайєрлса. Другий тип бар’єрів обумовлений локальними дефектами кристалічної решітки, котрі слугують центрами закріплення. Такими дефектами можуть бути не тільки поодинокі точкові дефекти, але й преципітати, мікровиділення іншої фази, вакансійно-домішкові скупчення.

Згідно теорії Пайєрлса енергія положення дислокації в кристалі визначається, так званим, потенціалом Пайєрлса, що змінюється з періодичністю решітки. В одному кристалі різним системам ковзання можуть відповідати різні потенціали або бар’єри Пайєрлса. У реальному кристалі енергетичний рельєф, по якому рухається дислокація (рельєф Пайєрлса), має вигляд складної сітчастої структури.

Процес термічного переходу дислокації з однієї долини потенціалу Пайєрлса в іншу схематично показано на рис.3.2. Він починається в результаті термічної флуктуації з перекидання в сусідню долину короткої ділянки дислокації. При цьому утворюються два різнойменні перегини (кінки), які розповсюджуються у двох протилежних напрямках. Процес руху перегинів визначається періодичністю решітки у напрямку їх розповсюдження. Потенціал, який відповідає напрямку руху перегинів, названо потенціалом Пайєрлса ІІ-го роду. Енергія та форма перегинів обумовлена висотою та формою потенціального рельєфу решітки. При розрахунках вони часто вибираються цілком емпірично.

Енергія активації руху дислокацій у напівпровідниках складається з енергії активації процесу утворення та енергії активації розповсюдження парних перегинів. На жаль, експериментально визначають лише загальну енергію активації руху дислокації. Точно визначити внесок кожної складової окремо неможливо. Результати дослідів з легованими кристалами вказують на те, що ці енергії сильно залежать від електронних станів перегинів.

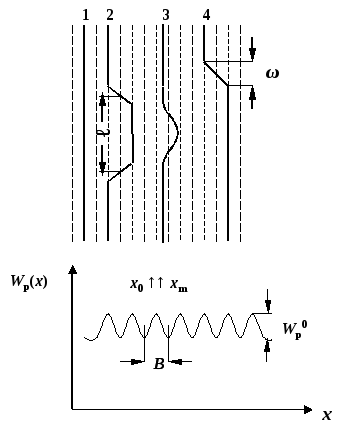
Рис. 3.2. Конфігурація лінії дислокації в періодичному потенціалі Wp(x) кристалічної решітки при утворенні подвійного (2, 3) та одиничного (4) перегинів: 1 – термічні флуктуації відсутні; 2 – подвійний перегин довжиною ℓ та шириною ω, який утворюється на дислокації за допомогою термоактиваційних процесів при  ≤ 0.1 p (p – напруження Пайєрлса); 3 – подвійний перегин при  > 0.1 p; 4 – одиничний перегин шириною ω біля поверхні кристалу при  << 0.1 p; Wp0 – енергія Пайєрлса; В – відстань між сусідніми долинами рельєфу Пайєрлса.

На практиці швидкість руху дислокацій описують емпіричною формулою, в якій шляхом підбору параметрів можна добитися не тільки якісного, але й кількісного збігу з результатами експерименту:

V = V₀·( / ₀) ^m ·exp(-E/kT), (3.1)

де Е – енергія активації руху дислокацій, яка дорівнює 1.5 еВ для германію та  2 еВ для кремнію, V₀ та ₀ деякі константи, m лежить у межах 1 - 2 у широкому інтервалі зовнішніх напружень (для Si m = 1.3÷1.45).

Однак, навіть перші експериментальні дослідження руху дислокацій, проведені на монокристалах кремнію та германію, які вважались найкращими модельними матеріалами для вивчення закономірностей руху дислокацій в рельєфі Пайєрлса, показали, що є істотні протиріччя між експериментальними даними та теоретичними розрахунками. Основні з них такі: експериментально спостережувані значення швидкостей руху дислокацій на два порядки перевищують розраховані значення. Не знаходить пояснення в рамках теорії Пайєрлса і факт існування стартових напружень для руху дислокацій, а також факт існування часів затримки початку їх руху.

Експериментально не виявлено залежності швидкості руху дислокацій від їх довжини (при довжинах ℓ > 100 мкм), яка передбачалась теорією Пайєрлса. Було одержано також сильний вплив електрично-активних домішок на швидкість руху дислокацій в монокристалах Si та Ge.

У зв’язку з існуванням вказаних протиріч були зроблені спроби удосконалити теорію Пайєрлса. Частково зняти їх вдалось лише в теоретичних роботах, які в явному вигляді враховують взаємодію рухомої дислокації з настільки потужними локальними перешкодами, що вони викликають довготривалу затримку та скупчення на них подвійних перегинів, що розповсюджуються по дислокації.

Експериментально також встановлено, що рухливість дислокацій пов’язана не тільки з особливостями пружної взаємодії з центрами закріплення, але й з ефектами електронного збудження кристалів, електроніки дефектів у напівпровідниках. Відомо, що дислокації в напівпровідникових кристалах є зарядженими і за умовою електронейтральності вони оточені областями просторового заряду (так званий циліндр Ріда [1]). Атмосфера точкових зарядів навколо дислокацій включає в себе і центри закріплення, які дислокація долає на початку свого руху. При електричному збудженні, зокрема, проходженні електричного струму через кристал, змінюється зарядовий стан центрів закріплення внаслідок їх часткової чи повної нейтралізації. Це обумовлює зміну потенціального бар’єру, зв’язаного з кулонівською взаємодією і проявляється в зміні енергії активації руху дислокацій у порівнянні з незбуреними кристалами.

В даній роботі передбачається вивчення руху дислокацій, що виникають навколо концентраторів напружень (подряпин) в кристалах кремнію та визначення енергії активації руху дислокацій. Крім того, пропонується дослідити вплив електричного струму на динамічну поведінку дислокацій в кристалах кремнію.