
- •По теории вероятностей
- •Содержание
- •Некоторые формулы комбинаторики
- •Случайные события. Классическое определение вероятности
- •Относительная частота события. Статистическое определение вероятности
- •Сложение вероятностей
- •Умножение вероятностей независимых событий
- •Зависимые события. Условная вероятность. Формула полной вероятности
- •Тогда нужная вероятность будет
- •Формула Бернулли
- •Формула Пуассона
- •Случайные величины
- •Закон распределения дискретной случайной величины
- •Числовые характеристики дискретной случайной величины
- •В частности, из свойств дисперсии следует, что
- •Найдем ее математическое ожидание, дисперсию и среднеквадратичное отклонение.
- •Биномиальный закон распределения дискретной случайной величины
- •Дискретной случайной величины
- •Непрерывной случайной величины. Плотность распределения
- •По определению
- •Воспользуемся формулой .
- •Числовые характеристики непрерывной случайной величины
- •Закон равномерного распределения вероятностей непрерывной случайной величины
- •Найдем функцию распределения .
- •Числовые характеристики равномерного распределения
- •Нормальный закон распределения непрерывной случайной величины
- •В дальнейшем нам потребуется интеграл Пуассона
- •Числовые характеристики нормального распределения
- •Функция Лапласа. Функция распределения случайной величины х, имеющей нормальное распределение
- •Вероятность попадания случайной величины х, имеющей нормальное распределение, в заданном интервале
- •Литература
Функция Лапласа. Функция распределения случайной величины х, имеющей нормальное распределение
В дальнейшем будем использовать функцию Лапласа, определяемую равенством
 .
.
Составлены подробные таблицы значений этой функции.
Укажем некоторые свойства функции Ф(х).
-
Ф(х) определена при всех значениях х.
-
Ф(0)=0.
3.
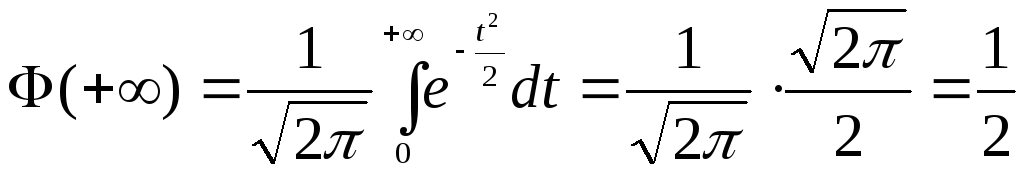 .
.
4.
![]() .
.
-
Ф(х) монотонно возрастает при всех
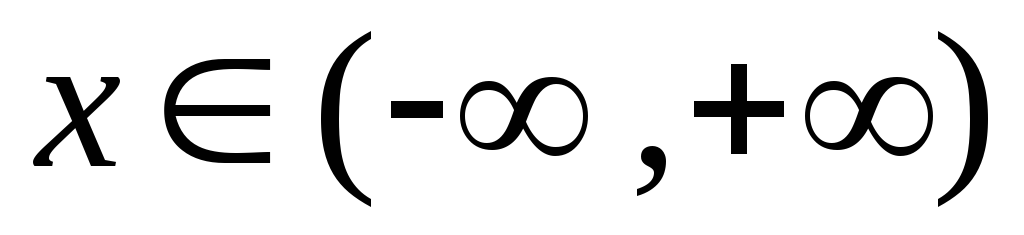 .
. -
Ф(х) – функция нечетная: Ф(-х)= - Ф(х).
Определим функцию распределения случайной величины Х, имеющей нормальное распределение.
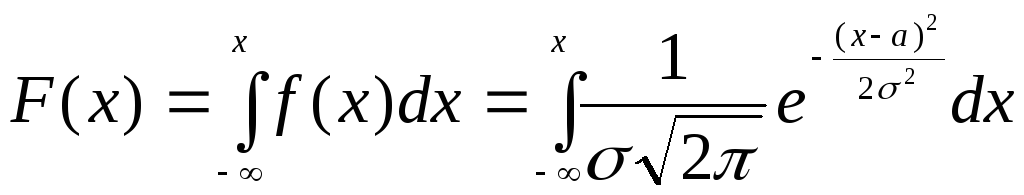 .
.
Обозначив
![]() получим
получим
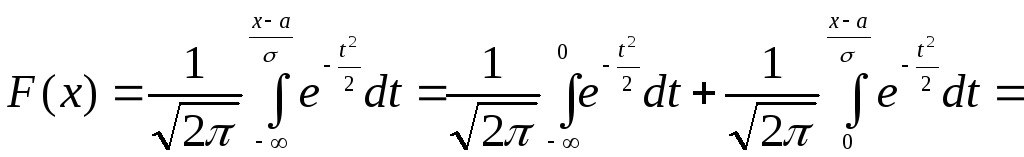
![]() .
.
Итак, функция распределения случайной величины Х имеет вид
![]() .
.
Вероятность попадания случайной величины х, имеющей нормальное распределение, в заданном интервале
Используя функцию распределения случайной величины Х, найдем вероятность попадания ее значений в интервал (α, β).
![]()
![]() .
.
Таким
образом,
![]() .
.
Пример.
Плотность распределения вероятностей
случайной величины Х
имеет вид
![]() .
Найти: γ,
M[X],
D[X],
F(x),
.
Найти: γ,
M[X],
D[X],
F(x),
![]() .
.
Случайная величина Х имеет нормальное распределение. Поэтому приведем плотность распределения f(x) к виду
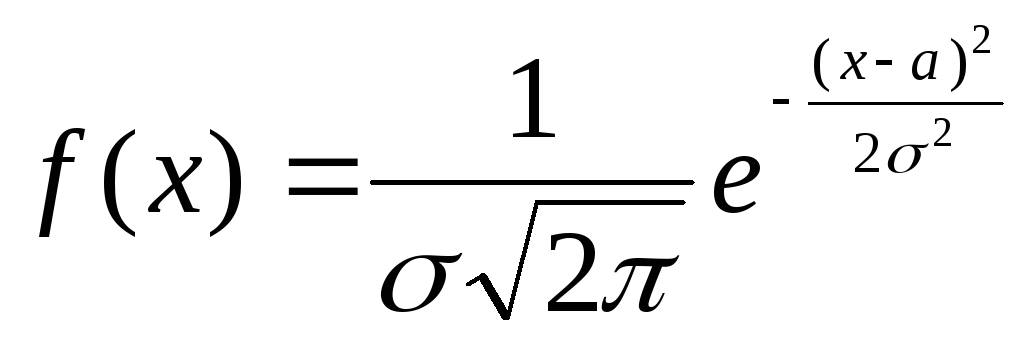 .
.
Выделим в показателе заданной функции полный квадрат
![]() .
.
Следовательно,
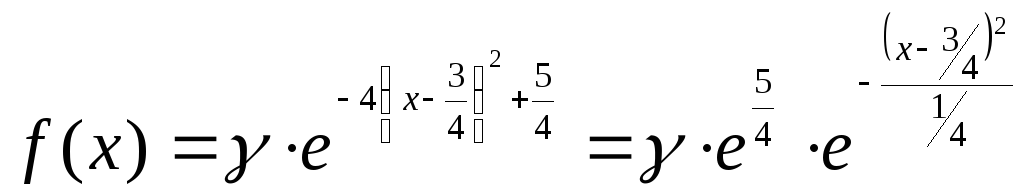 .
.
Сравним
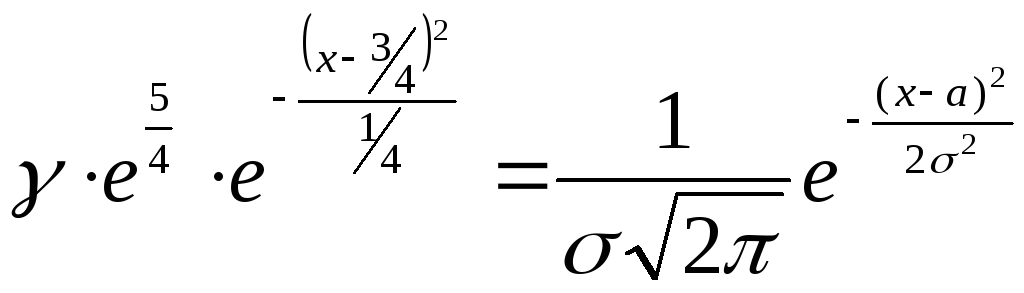 .
.
Из последнего равенства получаем
![]() .
.
![]() ,
т.е.
,
т.е.
![]() .
.
 ,
,
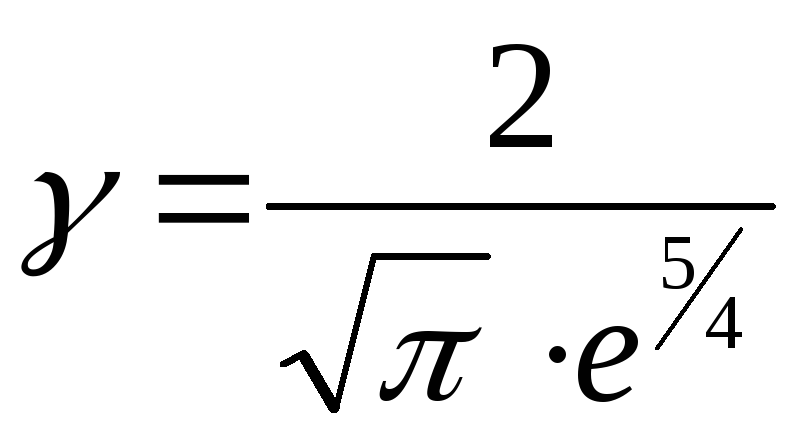 .
.
![]() .
.
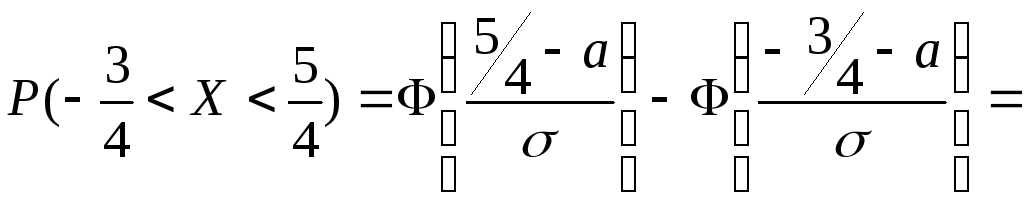
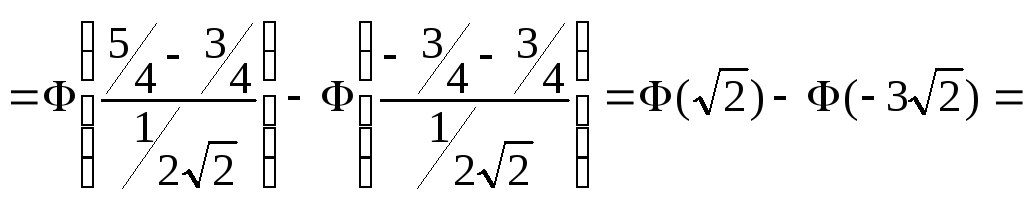
![]() .
.
В
последнем равенстве при вычислении
![]() и
и
![]() использованы таблицы значений функции
Ф(х).
использованы таблицы значений функции
Ф(х).
Итак:
 ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Литература
-
Пискунов Н.С. Дифференциальное и интегральное исчисления для ВТУЗОВ. М., 1962.
-
Гмурман В.Е. Теория вероятностей и математическая статистика.
-
Румшиский Л.З. Элементы теории вероятностей. М., 1966.
-
Севастьянов Б.А. Курс теории вероятностей и математической статистики. М., 1982.
-
Чистяков В.П. Курс теории вероятностей. М., 1982.
-
Гмурман В.Е. Руководство по решению задач по теории вероятностей и математической статистике. М., 1975.
