Дискретной случайной величины

Этот закон определяется формулой Пуассона

, где λ=np.

Случайная величина Х – число появлений события А в n испытаниях при большом n и малой вероятности р имеет распределение Пуассона

Х	0	1	2	…	n
Р				…

Можно показать, что для распределения Пуассона

M[X]= D[X]=λ=np.

Функция распределения

Непрерывной случайной величины. Плотность распределения

Рассмотрим непрерывную случайную величину Х, заданную а некотором интервале (а, b). Закон распределения вероятностей для такой величины должен позволять находить вероятность попадания ее значения в любой интервал (х₁, х₂).

Функция распределения непрерывной случайной величины Х называют функцию F(x), определяющую для каждого значения вероятность того, что случайная величина Х примет значение, меньшее х, т.е. .

Функция распределения обладает следующими свойствами:

1. Как любая вероятность .

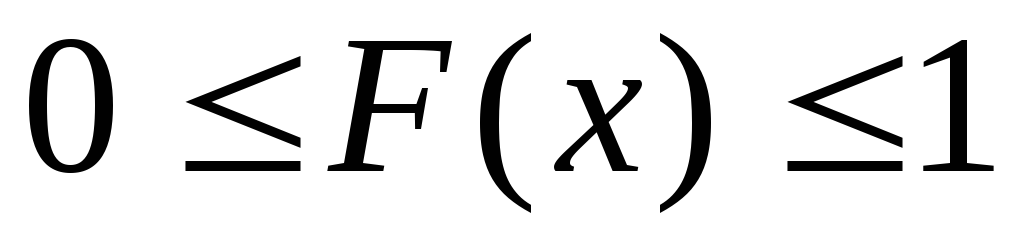2. F(x) – неубывающая функция, т.е. если х₁< х₂, то F(x₁)≤ F(x₂).

3. .

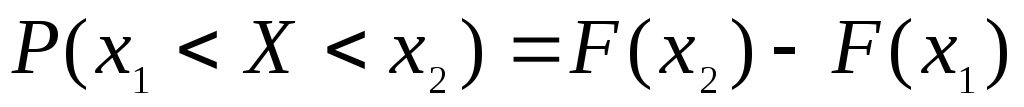4. Р(Х= x₁)=0.

5. Если все возможные значения случайной величины Х находятся на интервале (а, b), то F(x)=0 при х≤а и F(x)=1 при .

6. , .

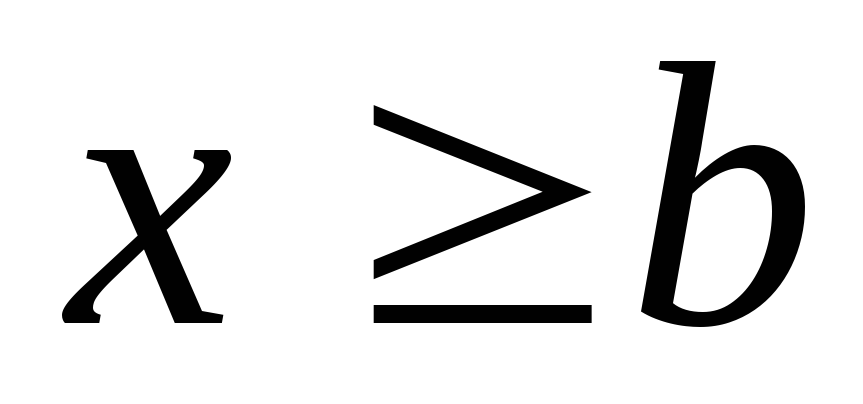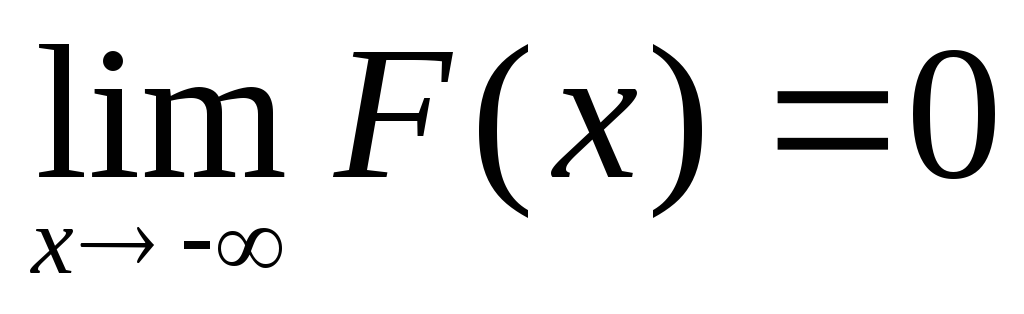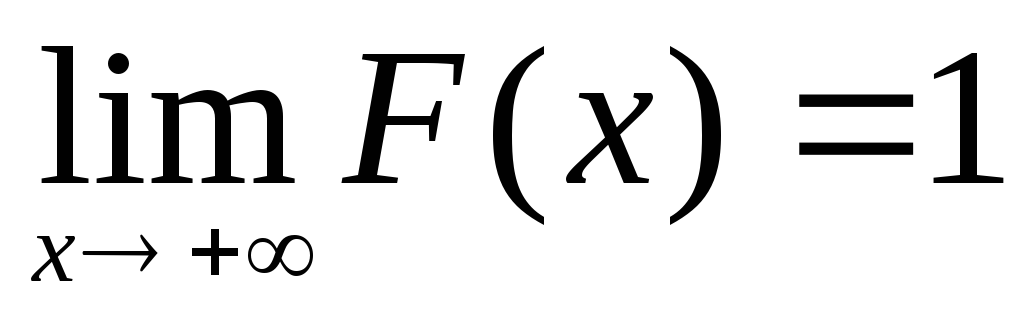Плотностью распределения непрерывной случайной величины Х называют производную от функции распределения: .

Плотность распределения непрерывной случайной величины Х обладает свойствами:

1. f(x)≥0.

2. .

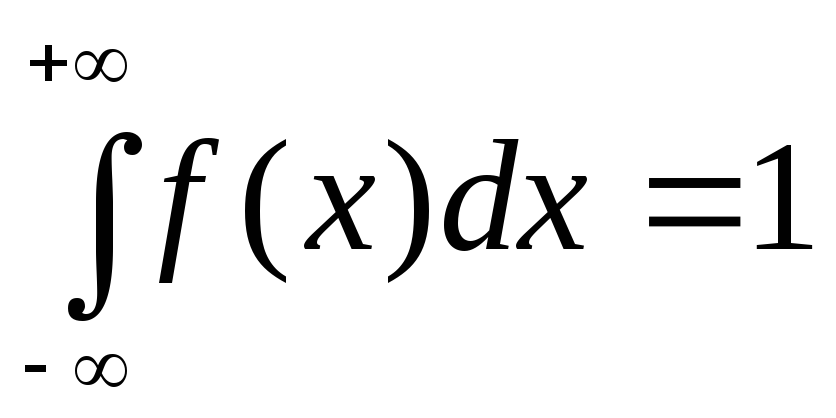3. Зная плотность распределения, можно найти функцию распределения случайной величины .

4. .

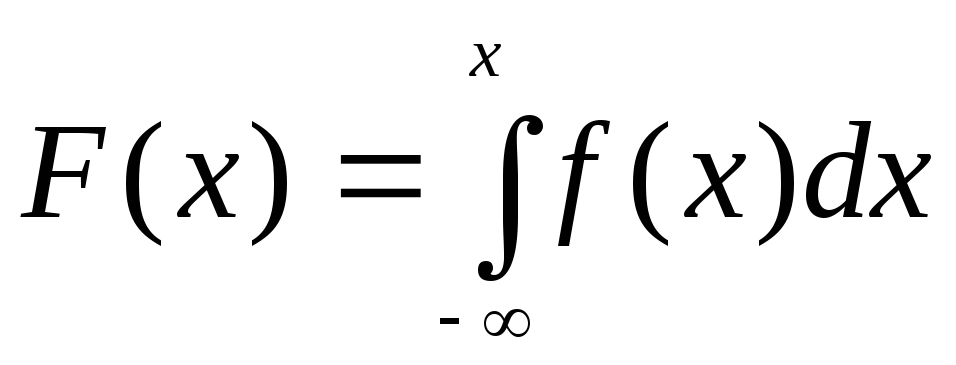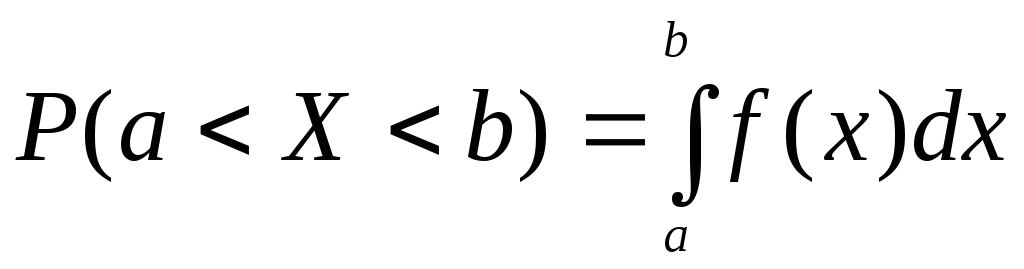Примеры. 1. Случайная величина Х задана функцией распределения

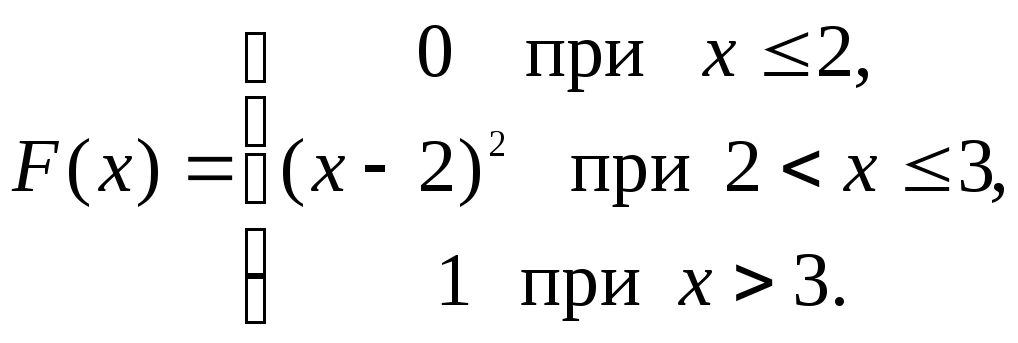
Найти плотность распределения этой случайной величины и вероятность попадания ее в интервал (1; 2,5).

По определению

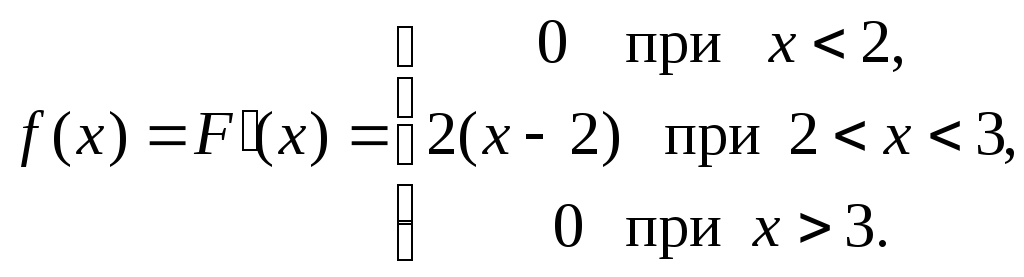
Требуемая вероятность будет

.

2. Дана плотность распределения непрерывной случайной величины Х:

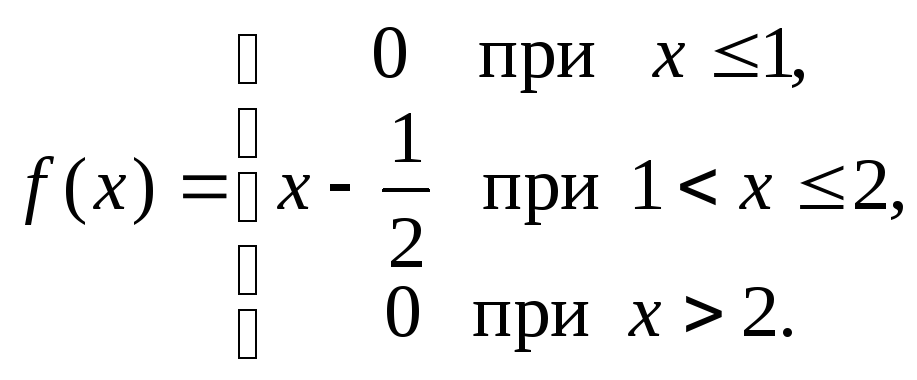
Найти функцию распределения этой величины.

Воспользуемся формулой .

Если х≤1, то f(x)=0, следовательно, .

Если 1<x≤2, то

.

Если х>2, то

.

Итак, искомая функция распределения имеет вид

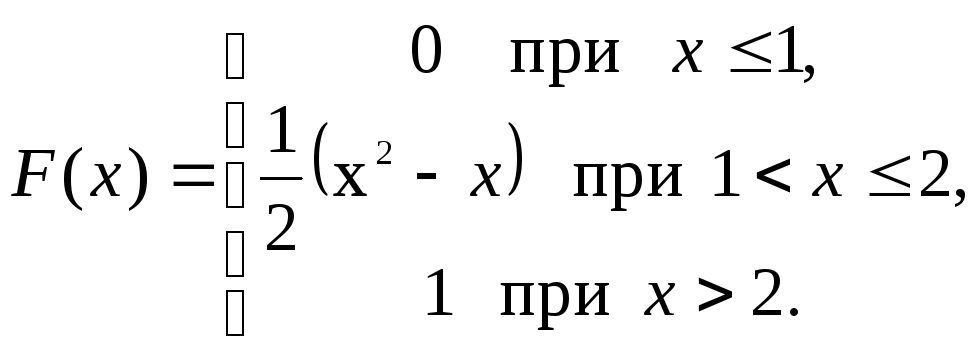
3. Составить функцию распределения F(x) дискретной случайной величины Х с законом распределения:

Х	2	4	7
Р	0,5	0,2	0,3

Если х≤2, то F(x)=0, так как значений меньших 2 величина Х не принимает. Поэтому при х≤2 F(x)=Р(Х<x)=0.

Если 2<x≤4, то F(x)=0,5, так как Х может принимать значение 2 с вероятностью 0,5.

Если 4<x≤7, то F(x)= Р(Х<x)= Р(Х=2)+ Р(Х=4)=0,5+0,2=0,7 (по теореме сложения вероятностей несовместных событий).

Если х>7, то F(x)=1, так как событие Х≤7 достоверное.

Итак, искомая функция распределения имеет вид

Числовые характеристики непрерывной случайной величины

Аналогично тому, как это было сделано для дискретной случайной величины, определим числовые характеристики непрерывной случайной величины Х с плотностью распределения f(x).

Математическим ожиданием непрерывной случайной величины Х с плотностью распределения f(x) называется выражение

.

Если случайная величина Х может принимать значения только на конечном отрезке [a, b], то .

Дисперсия непрерывной случайной величины Х определяется равенством

,

или равносильным равенством

.

Все свойства математического ожидания и дисперсии, указанные для дискретных величин, сохраняются и для непрерывных величин

Среднеквадратичным отклонением случайной величины Х называется корень квадратный из дисперсии

.

Значение случайной величины Х, при котором плотность распределения f(x) имеет наибольшее значение называется модой М₀[X].

Медианой М_е[X] непрерывной случайной величины Х, называют ее значение, определяемой равенством

или

.

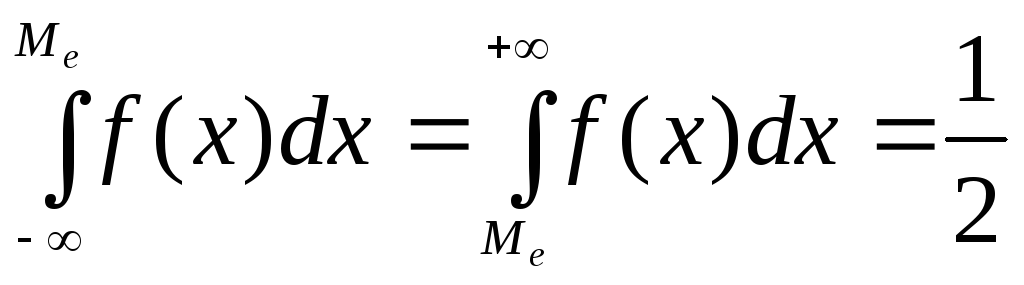Пример. Случайная величина Х задана плотностью распределения

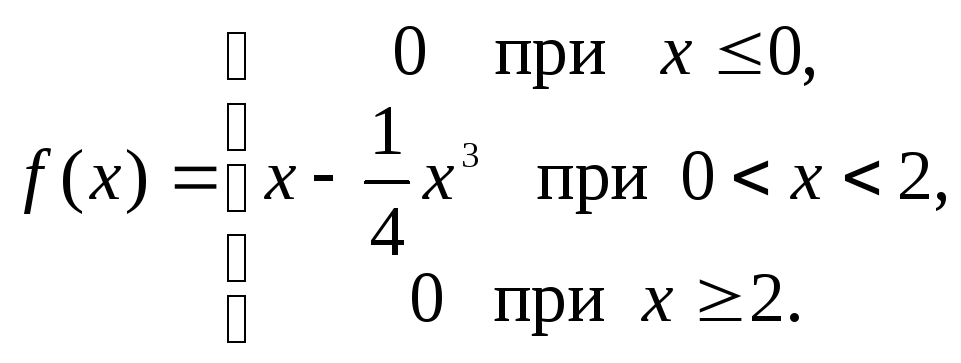
Найти математическое ожидание, дисперсию и среднеквадратичное отклонение величины Х.

Воспользуемся определениями.

.

.

.

.