4.2.Прямокутна система координат. Вектори, що задані своїми координатами

Нехай (рис. 4.3) три взаємно перпендикулярні прямі, які мають напрямки та масштаб. Для кожної точки простору існує її радіус-вектор , початок якого є початок координат , а кінець є дана точка .

Означення. Під декартовими прямокутними координатами точки розуміємо проекції її радіус – вектора на відповідні осі координат, тобто . Точка з координатами позначається через . Для знаходження координат точки треба побудувати прямокутний паралелепіпед з діагоналлю (рис.4.3).

Рис. 4.3

Довжина діагоналі паралелепіпеда: . Якщо позначити через кути, що утворені радіусом – вектором з координатними осями, то будемо мати

; .

Косинуси , , називаються напрямними косинусами радіус – вектора . Властивість їх легко доводиться:

.

Якщо у просторі задано вільний вектор , проекції його на осі в координати вектора

; ; .

Довжина вектора :

.

Напрямні косинуси можна знайти із рівнянь:

; ; .

Приклад. Знайти довжину на напрямок вектора .

Маємо

; ; .

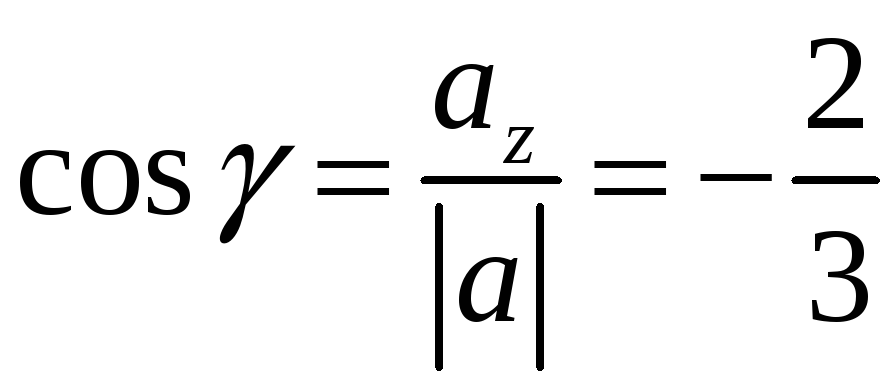Приклад. Знайти відстань між двома точками, що задані своїми координатами , . Нехай точка це початок відрізка , а його кінець (рис.4.4). Точки та можна задати їх радіусами – векторами та .

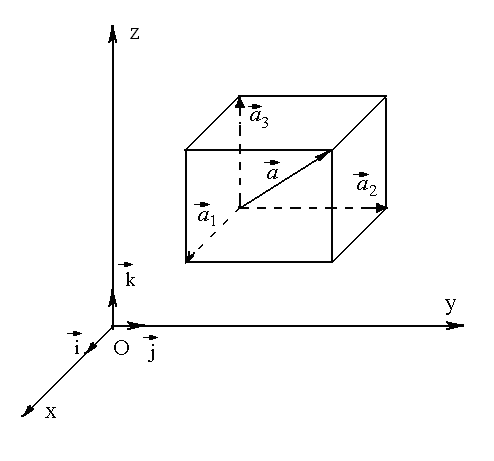
Рис.4.4. Рис.4.5.

Тоді вектор . Якщо цю векторну рівність спроектуємо на осі координат, то на основі властивостей проекцій будемо мати:

; ; .

Таким чином, довжина відрізка або довжина вектора буде:

.

Відзначимо основні дії над векторами, які задані координатами. Нехай вектор задано своїми проекціями на осі координат . Побудуємо паралелепіпед (рис.4.5), діагоналлю якого є вектор , а ребрами будуть його компоненти відносно відповідних координат осей. Маємо розклад: . Якщо введемо одиничні вектори осей (орти) , які напрямлені по осях координат, то на основі зв’язку між компонентами вектора та його проекціями будемо мати:

; ; .

Запишемо координатну форму вектора

.

Якщо вектор , то

.

Тоді розглянуті вище лінійні операції над векторами можна записати у такому вигляді:

1)

або

,

скаляр. Таким чином, при множенні вектора на скаляр координати вектора треба помножити на цей скаляр.

2)

або так:

.

Таким чином, при додаванні (або відніманні) векторів їх відповідні координати додаються (або віднімаються).

Приклад. Знайти координати точки , що ділить відрізок у відношенні (рис.4.6)

.

Нехай точками відповідають радіус-вектори . Тоді вектор , або

.

З цієї векторної рівності знайдемо вектор

,

або у координатах

.

Звідси, якщо відрізок точки поділити на дві рівні частини, то

.

Рис. 4.6

4.3. Скалярний добуток векторів та його властивості

Визначення. Скалярним добутком двох векторів та називається число, яке дорівнює добутку довжин даних векторів та косинусу кута між ними, тобто

, де .

На основі першої властивості проекції можна записати

.

Скалярний добуток має такі властивості:

1. .

2. .

3. .

4. .

5. , (скаляри).

З визначення скалярного добутку можна знайти косинус кута між двома ненульовими векторами

.

Скалярний добуток векторів можна записати у координатній формі. Нехай вектори задані так:

.

Знайдемо добуток цих векторів як многочленів (із властивостей скалярного добутку):

.

Для косинуса кута між векторами одержимо:

.

Умова колінеарності двох векторів

,

у координатах , або

.

Таким чином, вектори колінеарні тільки у тому випадку, коли їх відповідні координати пропорційні.

Для перпендикулярних векторів і /2) їх скалярний добуток дорівнює нулю.

.