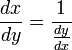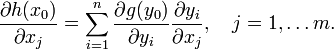- •Числовая последовательность
- •Определение
- •Примеры
- •Операции над последовательностями
- •Подпоследовательности
- •Примеры
- •Свойства
- •Предельная точка последовательности
- •Предел последовательности
- •Некоторые виды последовательностей
- •Ограниченные и неограниченные последовательности
- •Критерий ограниченности числовой последовательности
- •Свойства ограниченных последовательностей
- •Бесконечно большие и бесконечно малые последовательности
- •Свойства бесконечно малых последовательностей
- •Сходящиеся и расходящиеся последовательности
- •Свойства сходящихся последовательностей
- •Монотонные последовательности
- •Фундаментальные последовательности
- •Предел числовой последовательности
- •История
- •Определение
- •Обозначения
- •Свойства
- •Свойства Арифметические свойства
- •Свойства сохранения порядка
- •Другие свойства
- •Предел на бесконечности по Коши
- •Окрестностное определение по Коши
- •Обозначения
- •Свойства пределов числовых функций
- •Примеры
- •Бесконечно малая и бесконечно большая
- •Исчисление бесконечно малых и больших
- •Бесконечно малая величина
- •Бесконечно большая величина
- •Свойства бесконечно малых
- •Сравнение бесконечно малых
- •Определения
- •Примеры сравнения
- •Эквивалентные величины Определение
- •Теорема
- •Примеры использования
- •Исторический очерк
- •Замечательные пределы
- •Первый замечательный предел
- •Второй замечательный предел
- •Раскрытие неопределённостей
- •Числовой ряд
- •Определение
- •Операции над рядами
- •Критерий абсолютной сходимости
- •«O» большое и «o» малое
- •Определения
- •Обозначение
- •Другие подобные обозначения
- •Примеры использования
- •История
- •Непрерывная функция
- •Определения
- •Комментарии
- •Связанные определения Точки разрыва
- •Свойства Локальные
- •Глобальные
- •Полунепрерывность
- •Односторонняя непрерывность
- •Непрерывность почти всюду
- •Производная функции
- •Геометрический и физический смысл производной Тангенс угла наклона касательной прямой
- •Скорость изменения функции
- •Производные высших порядков
- •Способы записи производных
- •Примеры
- •Правила дифференцирования
- •Производная вектор-функции по параметру
- •Примеры
- •Касательная прямая
- •Строгое определение
- •Замечание
- •Касательная как предельное положение секущей
- •Касательная к окружности
- •Свойства
- •Вариации и обобщения Односторонние полукасательные
Примеры
-
Пусть f(x) = x2. Тогда
![]()
-
Пусть f(x) = | x | . Тогда если
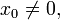 то
то
f'(x0) = sgn x0,
где sgn обозначает функцию
знака. Если x0 = 0, то
![]() а
следовательно f'(x0) не
существует.
а
следовательно f'(x0) не
существует.
Правила дифференцирования
Операция нахождения производной называется дифференцированием. При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций», то есть сложными функциями. Исходя из определения производной, можно вывести правила дифференцирования, облегчающие эту работу. Если C — постоянное число и f=f(x), g=g(x) — некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:
-
C' = 0
-
x' = 1
-
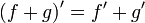 [2]
[2] -
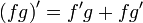 [3]
[3] -
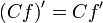
-
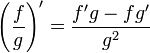 …(g
≠ 0)
…(g
≠ 0) -
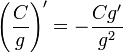 (g
≠ 0)
(g
≠ 0) -
Если функция задана параметрически:
![]() ,
то
,
то
![]()
Основная статья: Дифференцирование сложной функции
-
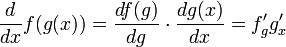
-
Формулы производной произведения и отношения обобщаются на случай n-кратного дифференцирования (формула Лейбница):
![]() где
где
![]() —
биномиальные
коэффициенты.
—
биномиальные
коэффициенты.
Следующие свойства производной служат дополнением к правилам дифференцирования:
-
если функция дифференцируема на интервале (a,b), то она непрерывна на интервале (a,b). Обратное, вообще говоря, неверно (например, функция y(x) = | x | на [ − 1,1]);
-
если функция имеет локальный максимум/минимум при значении аргумента, равном x, то f'(x) = 0 (это так называемая лемма Ферма);
-
производная данной функции единственна, но у разных функций могут быть одинаковые производные.
-
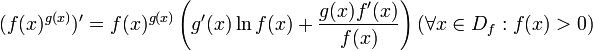
Доказательство
y = f(x)g(x)
ln y = g(x)ln f(x)
![]()
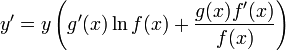
![]() ■
■
Таблица производных некоторых функций
Основная статья: Таблица производных
|
Функция
|
Производная
|
Примечание |
|
|
|
Доказательство:
Фиксируем
|
|
|
|
Доказательство:
Фиксируем
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Производная вектор-функции по параметру
Определим производную вектор-функции
![]() по
параметру:
по
параметру:
![]() .
.
Если производная в точке
![]() существует,
вектор-функция называется дифференцируемой
в этой точке. Координатными функциями
для производной будут
существует,
вектор-функция называется дифференцируемой
в этой точке. Координатными функциями
для производной будут
![]() .
.
Свойства производной вектор-функции (всюду предполагается, что производные существуют):
-
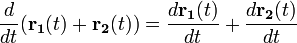 —
производная суммы есть сумма производных.
—
производная суммы есть сумма производных.
-
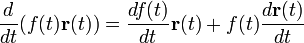 —
здесь
—
здесь
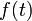 —
дифференцируемая скалярная функция.
—
дифференцируемая скалярная функция.
-
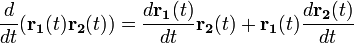 —
дифференцирование скалярного
произведения.
—
дифференцирование скалярного
произведения.
-
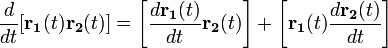 —
дифференцирование векторного
произведения.
—
дифференцирование векторного
произведения.
-
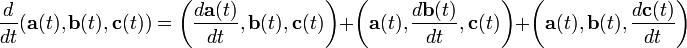 —
дифференцирование смешанного
произведения.
—
дифференцирование смешанного
произведения.
Таблица производных
Вычисление производной — важнейшая операция в дифференциальном исчислении. Эта статья содержит список формул для нахождения производных от некоторых функций.
В этих формулах f и g — произвольные дифференцируемые функции вещественной переменной, а c — вещественная константа. Этих формул достаточно для дифференцирования любой элементарной функции.
|
Содержание
|
Производные простых функций
Вывод
(cx)' = cx' = c
-
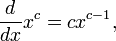 когда
когда
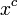 и
и
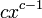 определены,
определены,
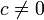
Вывод
(x + h)c = xc + (xc)'h + o(h)
(x + h)c − xc = (xc)'h + o(h)
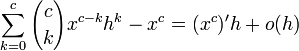
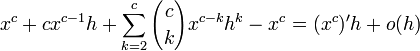
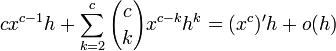
cxc − 1h + o(h) = (xc)'h + o(h)
![]()
cxc − 1 = (xc)'
Вывод
Так
как
![]() ,
то пусть
,
то пусть
![]() и
и
![]()
Тогда
![]()
Производные экспоненциальных и логарифмических функций
Вывод
![]()
Вывод
loga(x + h) = logax + (logax)'h + o(h)
loga(x + h) − logax = (logax)'h + o(h)
![]()
![]()
Производные тригонометрических и обратных тригонометрических функций
Вывод
sin(x + h) = sin x + (sin x)'h + o(h)
sin(x + h) − sin x = (sin x)'h + o(h)
![]()
![]()
(cos x)h + o(h) = (sin x)'h + o(h)
cos x = sin 'x
Производные гиперболических функций
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Правила дифференцирования общих функций
![]()
![]()
![]()
![]() (частный
случай формулы
Лейбница)
(частный
случай формулы
Лейбница)
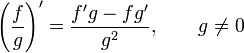
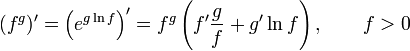
![]() —
Правило
дифференцирования сложной функции
—
Правило
дифференцирования сложной функции
![]()
![]()
Дифференцирование сложной функции
Цепное правило (правило дифференцирования сложной функции) позволяет вычислить производную композиции двух и более функций на основе индивидуальных производных. Если функция f имеет производную в точке x0, а функция g имеет производную в точке y0 = f(x0), то сложная функция h(x) = g(f(x)) также имеет производную в точке x0.
|
Содержание
|
Одномерный случай
Пусть даны функции, определённые в
окрестностях на числовой прямой,
![]() где
y0 = f(x0), и
где
y0 = f(x0), и
![]() Пусть
также эти функции дифференцируемы:
Пусть
также эти функции дифференцируемы:
![]() Тогда
их композиция также дифференцируема:
Тогда
их композиция также дифференцируема:
![]() и
её производная имеет вид:
и
её производная имеет вид:
![]()
Замечание
В обозначениях Лейбница цепное правило для вычисления производной функции y = y(x), где x = x(t), принимает следующий вид:
![]()
Инвариантность формы первого дифференциала
Дифференциал функции z = g(y) в точке y0 имеет вид:
![]()
где dy — дифференциал тождественного
отображения
![]() :
:
![]()
Пусть теперь
![]() Тогда
Тогда
![]() ,
и согласно цепному правилу:
,
и согласно цепному правилу:
![]()
Таким образом, форма первого дифференциала остаётся одной и той же вне зависимости от того, является ли переменная функцией или нет.
Пример
Пусть
![]() Тогда
функция
Тогда
функция
![]() может
быть записана в виде композиции
может
быть записана в виде композиции
![]() где
где
![]()
![]()
Дифференцируя эти функции отдельно:
![]()
![]()
получаем
![]()
Многомерный случай
Пусть даны функции
![]() где
y0 = f(x0), и
где
y0 = f(x0), и
![]() Пусть
также эти функции дифференцируемы:
Пусть
также эти функции дифференцируемы:
![]() и
и
![]() Тогда
их композиция тоже дифференцируема, и
её дифференциал имеет вид
Тогда
их композиция тоже дифференцируема, и
её дифференциал имеет вид
dh(x0) = dg(y0) * df(x0).
В частности, матрица Якоби функции h является произведением матриц Якоби функций g и f:
![]()
Следствия
-
Якобиан композиции двух функций является произведением якобианов индивидуальных функций:
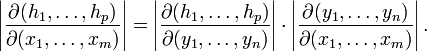
Для частных производных сложной функции справедливо
Производная обратной функции
Пусть
![]() -
дифференцируемая
функция от аргумента x в некотором
интервале
-
дифференцируемая
функция от аргумента x в некотором
интервале
![]() .
Если в уравнении
.
Если в уравнении
![]() y
считать аргументом, а x - функцией, то
возникает новая функция
y
считать аргументом, а x - функцией, то
возникает новая функция
![]() ,
где
,
где
![]() -
функция
обратная данной.
-
функция
обратная данной.
|
Содержание
|
Теорема (о дифференцировании обратной функции)
Для дифференцируемой функции с производной, отличной от нуля, производная обратной функции равна обратной величине производной данной функции, т.е
![]()
Доказательство
Пусть
![]() -
дифференцируемая функция,
-
дифференцируемая функция,
![]() .
Пусть
.
Пусть
![]() -
приращение независимой переменной y и
Δx
- соответствующее приращение обратной
функции
-
приращение независимой переменной y и
Δx
- соответствующее приращение обратной
функции
![]() .
Напишем
тождество
.
Напишем
тождество
![]()
Переходя в этом
равенстве к пределу при
![]() ,
которое влечет за собой стремление
,
которое влечет за собой стремление
![]() к
нулю (
к
нулю (![]() ),
получим:
),
получим:
![]() ,
где x'y
- производная обратной функции.
,
где x'y
- производная обратной функции.
Замечание Если пользоваться обозначениями Лейбница, то выше доказанная формула примет вид