Расчет вала вибратора на статическую прочность

Вал выполнен из стали 45 улучшенной. При диаметре вала d<120мм твёрдость поверхности HB269…302, , , , , , .

Рис. 15 Расчетная схема

Коэффициент запаса принимаем равным n_T=3.

Диаметр вала найдем из условия

, или

, где

- момент сопротивления изгибу, - максимальный изгибающий момент,

Принимаем.

Окончательно получаем ,

.

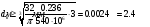Примем диаметр вала равным.

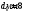
Расчет пружин

При осевом нагружении в пружине круглого поперечного сечения и малого угла подъема α возникают касательные напряжения τ, эпюра распределения которых по сечению дана на Рис.9 . Поскольку волокна элемента на внутренней стороне витка короче, чем на наружной, то углы сдвига при деформации пружины , а следовательно и напряжения в точке А будут больше, чем в точке В.

Наибольшее напряжение τ_мах возникает в точке А, расположенной на внутренней стороне витка, и его величина может быть определена по формуле

где К зависит от индекса пружины с =D/d .

Рис.16 эпюра касательных напряжений по сечению

Для пружины с малым углом подъема α=0-100 крутящий момент Мк=РD/2, полярный момент инерции круглого сечения

Wp=πd3/16, и формула примет вид:

где

Итак, расчет на прочность пружины может быть произведен по формуле

Тогда с=40/6=26,66 тогда посчитаем допустимое напряжение на кручение с коэффициентом запаса nT=1,5

тогда

Условие прочности выполнено.

Определение напряжений при сжатии пружин с витками малого угла подъема круглого поперечного сечения

При сжатии в пружине возникают касательные напряжения

где Р – вес конструкции, действующей на пружину.

В нашем случае на пружину действует вес траверсы и двух вибраторов, прикреплённых к траверсе.

Тогда напряжения

Расчет пружин на усталость

Рисунок 17

F₁=22H; F₂=209H;

D₁=46 мм; D₂=34 мм; D =40 мм; d=6 мм;

l₁= 75,4мм; l₂= 62,3мм; l₀=76,7 мм;

Коэффициент запаса

,

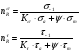где - коэффициенты снижения предела выносливости;

, , , , ;

, - амплитудное значение цикла;

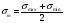, - среднее значение;

Тогда

.

Так как пружина изготовлена из стали 365С2ВА, то

Максимальные и минимальные напряжения определяются из учёта приложенной нагрузки. В нашем случае, касательные напряжения возникают от приложенного момента и силы веса, а нормальные напряжения – от того же момента и от сдвигающей силы.

Рассмотрим отдельно напряжения, возникающие от момента:

нормальные

.

касательные

.

Максимальные касательные и минимальные нормальные напряжения возникают при :

.

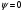Минимальные касательные и максимальные нормальные напряжения возникают при

.

С учётом напряжений от сдвигающей силы и от силы веса

.

Тогда

, .

С учётом полученных результатов коэффициент запаса

.

Список литературы

1. Дунаев П.Ф., Леликов О.П. Конструирование узлов и деталей машин. Л., Высшая школа, 2000.

2. Л.П. Варламова, И.А. Огринчук Выполнение курсовых проектов на кафедре «Детали машин», учебное пособие, часть 1, Цилиндрические соосные, цилиндровервячные и конические передачи. М., МГТУ им Н.Э. Баумана, 1985г.

3. Тибанов В.П., Варламова Л. П. Методические указания к выполнению домашнего задания по разделу «Соединения». М., МГТУ им. Н.Э. Баумана, 1999.

4. Детали машин. Атлас конструкций. Часть 1, 2. Под ред. Решетова Д.Н. М., Машиностроение, 1992.

5. Иванов В. Н., Баринова В. С. Выбор и расчеты подшипников качения. М., МВТУ, 1988

6. «Подшипники качения», справочник. Под редакцией В.Н.Нарышкина. Издательство «Машиностроение».

7. В.Л.Бидерман “Прикладная теория механических колебаний”. Издательство “Высшая школа” Москва-1972г.

Стр. 24