Расчет траверсы на изгиб

Рис. 9 Расчетная схема.

Напряжения: ,

1. для прямоугольного сечения

Рассмотрим вариант с l=500мм, h=2a

Где - момент сопротивления сечения траверсы.

Траверса изготовлена из стали 40Х, для которой после термической обработки 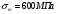. Коэффициент запаса по текучести

2. для двутаврого сечения

Рассмотрим вариант с l=500мм, h=2a, s=3мм

Выбираем двутавровое сечение траверсы, длина траверсы l=500мм, h=2a, s=3мм, а=38.8мм

Расчет вибратора

Вибратор служит для получения возмущающей силы, необходимой для создания вынужденных колебаний в колебательной системе.

Вынуждающий момент на траверсе: .

Усилие, необходимое для создания в образце напряжения

,

где - масса вибратора, кг;

- объём неуравновешенной массы, м³;

h – высота неуравновешенных масс, м;

– расстояние от оси неуравновешенной массы до её центра масс, м.

рис. 10 Схема массы вибратора

Расстояние от оси неуравновешенной массы до центра масс определяем следующим образом:

, где

- статический момент большей площади, м³;

- статический момент меньшей площади, м³;

- площадь неуравновешенной массы, м².

Тогда

.

Тогда

.

Для определения высоты неуравновешенной массы воспользуемся тем, что

.

Принимаем толщину неуравновешенной массы h=0,008 м, =0,008 м, тогда

=0,021 м

По полученным размерам вибратора его масса получается равной

Уточненный расчет вибратора (лист 2)

Рис. 11 Расчетная схема

Инерционная сила остается постоянной

, а значит и .

Значение новой высоты неуравновешенных масс

, где

h_в- высота неуравновешенной массы с вырезом, находящаяся посередине,

h_бв - высота двух неуравновешенных масс с вырезом, находящиеся по бокам.

h_в определим из соотношения , где

- статический момент инерции площади, находящейся посередине.

У нас r₁=8 мм, r₂=21 мм.

Примем , . Тогда получаем ,

,

Высоту найдем из условия , получаем

.

Высоту h_бв найдем из соотношения , где

- статический момент инерции площади с вырезом.

,

Из окончательно находим h_бв

.

Суммарное значение высоты неуравновешенных масс

.

Уточненный расчет траверсы

Рис. 12 Уточненный вид траверсы.

Масса одного вибратора m=0,027 кг.

Будем считать, что вибратор имеет форму цилиндра.

Крепление образца в траверсе представляет собой тонкостенную коробку.

Найдем уточненные размеры траверсы.

Расстояние между дальними точками двутаврового сечения 0,48 м.

Получили расстояние между осями вибраторов равное 0,6 м

Рассчитаны размеры уравновешивающей массы

Рис. 13 Уравновешивающая масса.

Расчет подшипников вибратора

Рис. 14 Расчетная схема.

где - усилие в вибраторе;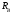и - реакции в опорах подшипников.

Предположим, что подходит шариковый радиальный однорядный подшипник особо легкой серии №18 по ГОСТ 8338. У него:

Наиболее нагруженной является опора Г, следовательно весь дальнейший расчёт будет производится по этой опоре.

Проведём расчёт по динамической грузоподъёмности .

Эквивалентная динамическая радиальная нагрузка подшипника в опоре Г при постоянном режиме нагружения:

где - т.к. вращается внутреннее кольцо подшипника;

- коэффициент безопасности, учитывающий влияние перегрузок на ресурс подшипника;

- температурный коэффициент.

Проверим, можно ли пользоваться уравнением долговечности:

- верно.

Проверим подшипники по статической грузоподъёмности.

Учтём переменный режим нагружения: где - коэффициент эквивалентности, учитывающий типовой режим нагружения.

По уравнению долговечности:

где L – ресурс подшипника;

- коэффициент усиления работы,

a₂ – коэффициент, учитывающий особенности металла и конструкции подшипника;

a₃ – коэффициент, учитывающий характер смазки и наличие перекосов.

Найдем по уравнению долговечности требуемую грузоподъёмность:

Так как у подшипника №18 ,то выбранный нами подшипник подходит.