Задание для самостоятельной работы
Найти решение методом Гаусса(в двух вариантах) следующих систем линейных алгебраических уравнений:
№1
Ответ:
№2
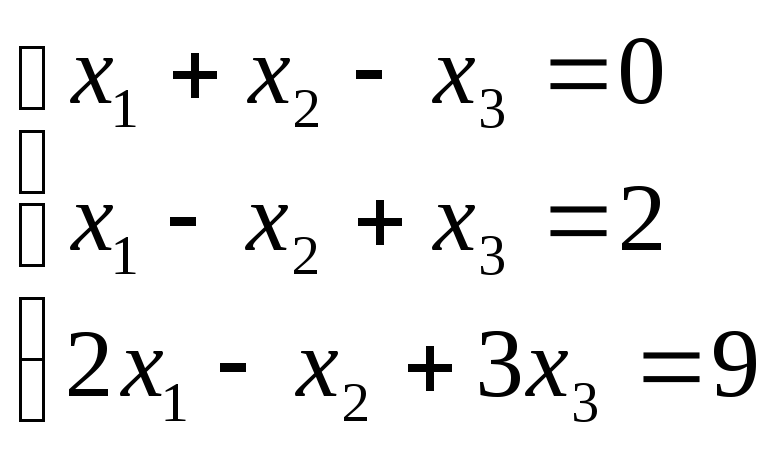
Ответ:
№3
Ответ:
№4
Ответ:
№5
Ответ:
№6
Ответ:
№7
Ответ:
Существо метода Крамера
В отличие от метода Гаусса метод Крамера применяется к системам, у которых число уравнений совпадает с числом неизвестных.
Пусть дана система из n линейных уравнений с n неизвестными:
В матричной форме её можно записать так: A*X=B.Основная матрица такой системы квадратная. Определитель данной матрицы выглядит так
det A=
Он называется определителем системы.
Если
,
то система невырождена.
Отыщем решение приведенной выше
системы уравнений при условии
в матричной форме A*X=B,
где А-матрица коэффициентов
,
а В-матрица свободных членов
.Для
этого умножим обе части матричного
уравнения слева на обратную матрицу
.
Получим
.
Так как
(единичная
матрица), а
,
полученное уравнение преобразуется к
виду
.
Это так называемый матричный способ
решения систем уравнения . Напомним,
что
,
где
-
союзная матрица –матрица, составленная
из алгебраических дополнений
Используя матричное равенство
и выражение для обратной матрицы
легко показать, что в этих уравнениях
детерминанты
получены из det A
заменой соответствующего столбца
коэффициентов столбцом свободных
членов.
Например,
.
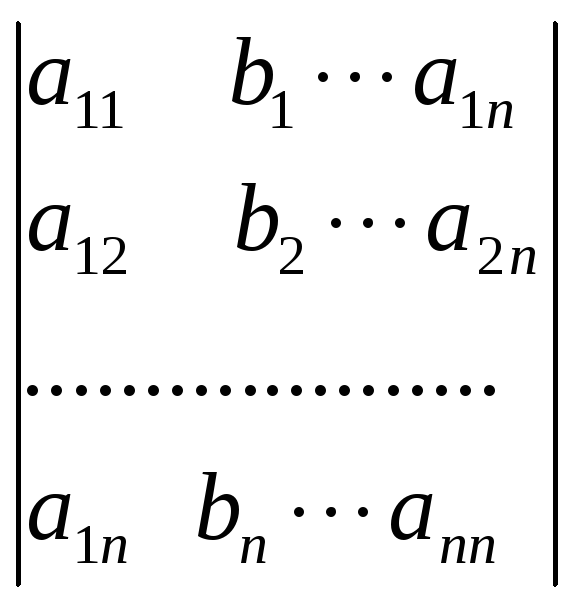Решение невырожденных систем линейных уравнений методом Гаусса
Эти формулы называются формулами
Крамера. В компактной форме они
записываются так:
где
i-меняется от 1 до n.
Примеры:
№1
Исследовать на совместимость и найти решение системы , приведенных ниже уравнений методом Крамера:
Решение:
Для определения совместности нужно найти ранг матрицы коэффициентов и ранг расширенной матрицы (теорема Кронекера - Капелли).
1.Составим основную и расширенную матрицу системы:
2.Определим ранг матрицы коэффициентов( основной матрицы). Для этого вычислим её определитель:
Отсюда следует, что rang A=2.
3.Теперь определим ранг расширенной
матрицы rang
.
Определителя у этой матрицы не существует, поскольку она не квадратная.
4.Тогда найдем и вычислим её миноры 2-ого
порядка. Их общее число - три
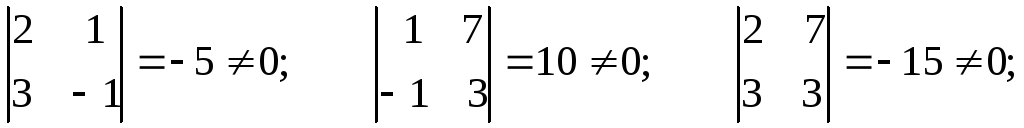
Все они не равны нулю.
Таким образом, rang
=2.
Следовательно, rang
=rang
A. Значит , система совместна.
Решим систему методом Крамера. Для этого
из определителя det A
получим детерминант
заменой
1-ого столбца на столбец свободных
членов:
Значит,
6. Из определителя det A
путём замены 2-ого столбца столбцом
свободных членов определим
:
Отсюда следует, что
7. Проверка:
7=7; 3=3, то есть, получаем верные равенства.
Ответ:
№2
Исследовать на совместимость и решить систему методом Крамера:
Решения:
Для определения совместности нужно найти основной и расширенной матриц.
1.Составим основную A и
расширенную
матрицы:
2.Определим ранг матрицы коэффициентов (основной матрицы). Для этого вычислим её определитель:
Отсюда следует, что rang A=3.
3.Определим ранг расширенной матрицы
(rang
).
Для чего сначала вычислим её миноры
третьего порядка. Их общее число -
четыре
.
Все они не равны нулю.
Таким образом, rang
=3.
Следовательно, rang A=rang
.
Это значит, что исследуемая система
совместна.
4.Решим данную систему методом Крамера.
Для этого из определителя det
A получим детерминант
заменой
1-ого столбца на столбец свободных
членов:
Значит,
5. Из определителя detA путём
замены 2-ого столбца столбцом свободных
членов, получаем детерминант
:
Значит,
6. Из определителя det A
путём замены 3-ого столбца столбцом
свободных членов определим
:
Значит,
Проверка:
Подставляем найденные значения неизвестных в исходную систему:
Получаем верные неравенства: 0=0
2=2
9=9
Ответ: