Решение:

Этим методом решение осуществляется путём последовательного исключения неизвестных из системы уравнений.

Приведём систему к ступенчатому виду. Для этого используем следующие элементарные преобразования системы. Из второго уравнения почленно вычтем первое уравнение, умноженное на 2.Затем из третьего уравнения вычтем первое, умноженное на 3, а из четвертого уравнения вычтем первое уравнение, умноженное на 5.

Получим:

Разделим обе части третьего уравнения на (-2), а четвертого на (-6).

Получим: Систему вида:

Она имеет единственное решение, которое является точнее решением исходной системы.

Получим решение заданной системы другим способом, т.е. в матричном виде. Для этого составим её расширенную матрицу:

Подвергнем её элементарным преобразованиям , приводящим к эквивалентным матрицам. С использованием первой строки преобразуем следующие. Для этого из второй строки вычтем первую, умноженную на 2.

Далее из третьей строки вычтем первую, умноженную на 3

Из четвертой строки вычтем первую, умноженную на 5

Затем с использованием второй строки преобразуем все оставшиеся. Для этого к третьей строку прибавим вторую, умноженную на 2.

К четвертой строке прибавим вторую, умноженную на 6.

Теперь воспользуемся третьей строкой, а именно к четвертой строке прибавим третью, умноженную на (-3)

Полученной матрице соответствует система:

Осуществляя, соответствующие подстановки, получим:

Таким образом, обоими способами получены одни и те же решения.

Произведем проверку, подставляя полученные значения неизвестных в исходную систему:

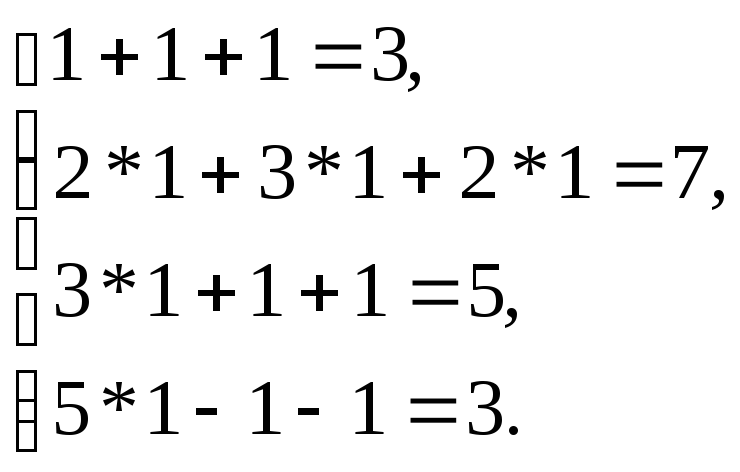
Получаем верные равенства :3=3

7=7

5=5

3=3

Ответ:

№2

Решить методом Гаусса ( в двух вариантах)следующую систему линейных алгебраических уравнений:

Решение

Приведем систему к ступенчатому виду, то есть исключим неизвестное из всех уравнений кроме первого. Для этого используем элементарные преобразования заданной системы, из второго уравнения вычтем первое, умноженное на 3;Из третьего уравнения вычтем первое, умноженное на 2; Из четвертого уравнения вычтем первое, умноженное на 2.

Получим систему:

Теперь с использованием второго уравнения преобразуем третье и четвертое уравнение системы, к третьему уравнению прибавим второе, умноженное на (-1), к четвертому уравнению прибавим второе, умноженное на (-3/4);

Получим:

Из четвертого уравнения вычтем третье, умноженное на 2/4:

Получим конечную ступенчатую форму исходной системы и её единственное решение.

Осуществим решение заданной системы другим способом.

Для этого составим её расширенную матрицу:

Подвергнём её элементарным преобразованиям, приводящим к эквивалентным матрицам, из второй строки вычтем первую, умноженную на 3:

Из третьей строки вычтем первую, умноженную на 2:

;

Из четвертой строки вычтем первую строку, умноженную на 2:

,

Теперь воспользуемся для элементарных преобразований второй строкой,

из третьей строки вычтем вторую строку, умноженную на 1:

;

Из четвертой строки вычтем вторую, умноженную на ¾:

Далее воспользуемся третьей строкой, а именно, из четвертой строки вычтем третью, умноженную на 2/4:

Полученной матрице соответствует система:

Совершая подстановки, получим:

Проверка:

Получим верные неравенства: 5=5

0=0

9=9

-1=-1

Ответ: