Решение:

По теореме Кронекера – Капелли система совместна только тогда, когда rang A=rang

Находим rang A и rang и затем исследуем на совместимость систему.

1.Запишем основную и расширенную матрицу:

2.Вичислим миноры основной матрицы. Она имеет три столбца, поэтому в первую очередь ищем определители третьего порядка. Их общее число- четыре

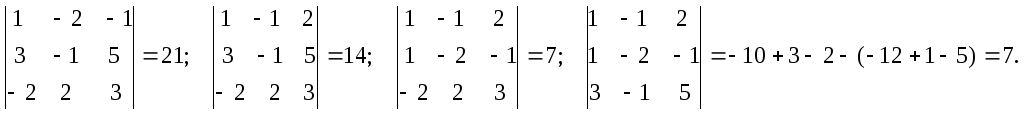
Все миноры третьего порядка не равны нулю.

Значит rang A=3.

3.Для определения rang Вычислим миноры расширенной матрицы. Она имеет четыре строки и столбца. Поэтому в первую очередь вычислим её определитель четвертого порядка:

det A=

Он не равен нулю. Значит rang =4.

Вывод: Так как rangA rang , то по теореме Кронекера – Капелли, эта система несовместна.

Задание для самостоятельной работы:

Показать, что система совместна( или несовместна)используя теорему Кронекера – Капелли :

№1

Ответ: система совместна.

№2

Ответ: система совместна.

№3

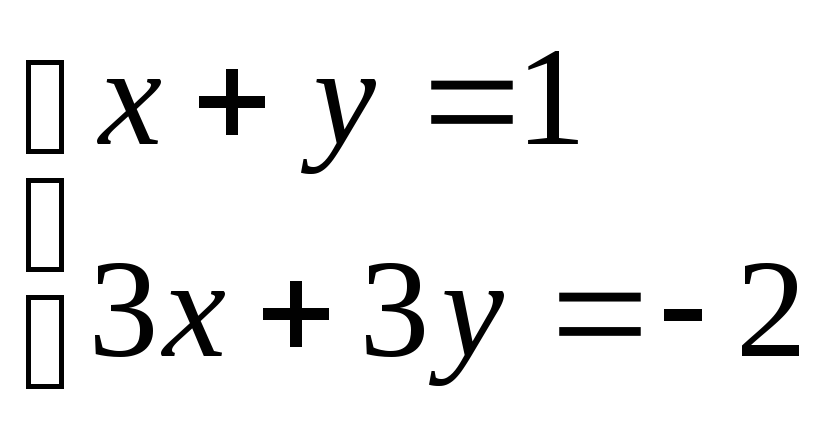
Ответ: система несовместна.

№4

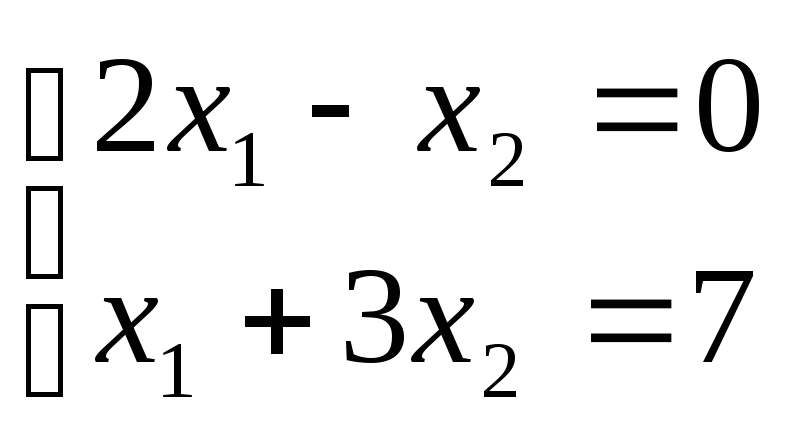
Ответ: система совместна

№5

Ответ: система совместна.

Решение систем линейных алгебраических уравнений методом Гаусса.

Решение системы линейных уравнений методом Гаусса является одним из самых универсальных и эффективных методов решения систем линейных алгебраических уравнений.

Осуществляется он путем последовательного исключения неизвестных из системы уравнений.

Пусть дана следующая система линейных алгебраических уравнений, содержащая n-неизвестных и m-уравнений:

Процесс решения таких систем по методу Гаусса состоит из двух этапов:

На первом этапе: система приводится к ступенчатому , в частности , к треугольному виду. В ступенчатой форме система может быть записана следующим образом:

В ней , коэффициенты и называется главными элементами системы.

На втором этапе: из этой ступенчатой системы последовательно определяются неизвестные.

Существо метода Гаусса.

Будем считать, что элемент , если он равен нулю, то первым в системе уравнений запишем то из них, у которого коэффициент перед неизвестным отличен от нуля. Преобразуем систему, исключив неизвестное .Из всех уравнений, кроме первого. Для этого используем элементарное преобразование системы. Например, обе части первого уравнения домножим на величину и сложим почленно со вторым уравнением системы.

Затем обе части первого уравнения умножим на величину . И сложим с третьим уравнением.

Продолжая эту процедуру(насколько возможно), из исходной системы получаем эквивалентную ступенчатую систему вида, показанной ниже:

В ней коэффициенты и свободные члены– это новые значения, полученные после исключения из уравнений системы неизвестного.

Аналогичным образом, считая главным элементом коэффициент исключаем из уравнений системы неизвестное, кроме первого и второго уравнений.

То же самое осуществляется для неизвестных и т.д.

Процедура длится пока она возможна . Если в процессе приведения системы к ступенчатому или треугольному виду появляются уравнения типа:0=0, то такие уравнения отбрасываются. Если же в процессе приведения системы к ступенчатому виду появятся уравнения типа:0=, где , то это будет свидетельствовать о том, что система уравнений заданного вида несовместна. В этом существо первого этапа.

Второй этап: заключается в решении ступенчатой системы уравнений. Отметим, что , вообще говоря, любая ступенчатая система имеет бесконечное множество решений. Для получения общего решения системы в последнем её уравнении выражаем первое неизвестное через все остальные:. Затем полученное значение подставляем в предыдущее уравнение и выражаем неизвестное через. Продолжаем эту процедуру до определения через неизвестные . Получаем общее решение ступенчатой системы. Затем свободным неизвестным присваиваем некоторые призвольные значения. В результате этого получаем одно из частных решений. Задавая новые произвольные значения свободных неизвестных , получаем второе, третье и др. частные решения.

Замечание 1:если ступенчатая система оказывается треугольной , т.е k=n,то она имеет единственное решение .

Замечание 2:на практике удобнее работать не с системой уравнений, а с соответствующей ей расширенной матрицей .При этом только над её строками осуществляются элементарные преобразования. Удобно также, когда первая строка расширенной матрицы начинается с единицы. Если это не так, то переставляют строки , добиваясь желаемого результата , либо обе части первого уравнения системы делят напри условии, что .

Примеры:

№1

Решить методом Гаусса(в двух вариантах)следующую систему линейных алгебраических уравнений: