Математика. Лекция №7

1.1 Кривые второго порядка

1.1.1 Окружность – геометрическое место точек, равноудалённых от одной данной точки (центра). Пусть С(a,b)– центр окружности, R– её радиус, а М(х,у) – произвольная точка окружности. R = СМ. Тогда

СМ = , или

= R² – уравнение окружности

В частным случае, если С (a,b)= О (0,0), то уравнение окружности примет вид:

х² +у² = R² (1)

Для точки М(х,у), лежащей внутри окружности получим:

< R²

для точки М(х,у), лежащей вне окружности:

> R²

1.1.2 Эллипс

И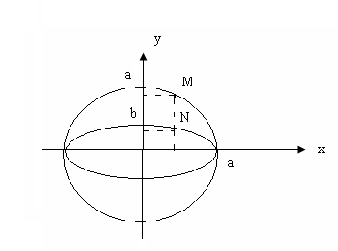з формулы (1) следует: . Знак «+» соответствует верхней полуокружности,

«-» - нижней.

Будем сжимать окружность следующим образом: из точки

М(х; ) будем получать точку

N(x,. Тогда ордината точки N будет составлять некоторую часть от ординаты точки М (b< a). Так, например, точка (0; а) перейдёт в точку (0; ) = (0; b). Все точки N образуют геометрическое место точек эллипса. Построение эллипса – сжатие окружности к горизонтальному диаметру. Из построения получим, что точки эллипса должны удовлетворять уравнению:

– каноническое уравнение эллипса

a – большая полуось, b – малая. Оси симметрии эллипса называются его осями, точки пересечения осей с эллипсом – вершинами эллипса.

О форме эллипса говорит эксцентриситет:

При b = a e =0. Т.е. окружность – это эллипс с нулевым эксцентриситетом.

Эллипс можно задать, как геометрическое место точек, сумма расстояний от каждой из которых до двух данных точек F и F₁ (фокусов) постоянно и равно 2а (рисунок 1).

Рисунок 1.

При этом расстояния

Если a < b, т.е. большой полуосью является b, то фокусы находятся на оси Оу и при этом:

Директрисы эллипса – прямые, определяемые формулами:

(если a > b) и

1.1.3 Гипербола

Гипербола - геометрическое место точек, разность расстояний от каждой из которых до двух данных точек F и F₁ (фокусов) постоянно и равно 2а (рисунок 2). 0<2a<FF₁.

– каноническое уравнение гиперболы (2)

Рисунок 2.

Осями симметрии гиперболы, заданной уравнением (2) являются оси координат, а – вещественная (действительная) полуось, b – мнимая. Ось Ох пересекает гиперболу в точках А(а;0) и А₁(-а;0) – вершинах гиперболы. с = OF=OF₁

>1 – эксцентриситет гиперболы

Прямые - асимптоты гиперболы

Ветви гиперболы подходят к асимптотам бесконечно близко, но не пересекаются с ними.

Фокальные радиус-векторы произвольной точки М(х; у) определяются формулами:

Гиперболы и называются сопряжёнными. Если гипербола задана уравнением , директрисы гиперболы – прямые, заданные уравнениями:

Если гипербола задана уравнением , директрисы гиперболы задаются уравнениями:

1.1.4 Парабола

Парабола – геометрическое место точек, каждая из которых равноудалена от данной точки F (фокуса) и от данной прямой (директрисы).

Канонические уравнения:

1). Для параболы, симметричной относительно Ох (рисунок 3)

(3)

Фокус параболы F лежит на оси Ох, директриса имеет уравнение

Фокальный радиус-вектор точки М (х; у)

2). Для параболы, симметричной относительно Оу (рисунок 4) каноническое уравнение: (4)

Фокус параболы F лежит на оси Оу, директриса имеет уравнение

Фокальный радиус-вектор точки М (х; у)

Рисунок 3. Рисунок 4.

Каноническое уравнение задаёт параболу, вершина которой находится в начале координат.