- •1 Таганрог 2011
- •1. Изучаемое физическое явление:
- •2. Формулировка поставленной задачи:
- •3. Таблица характеристик измерительных приборов:
- •4. Описание лабораторной установки и вывод расчетных формул.
- •5. Результаты измерений и их обработка.
- •6. Формулы для оценки погрешностей косвенных измерений.
- •7. Запись окончательного результата.
ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ
ЮЖНОГО ФЕДЕРАЛЬНОГО УНИВЕРСИТЕТА
Кафедра физики
Лабораторная работа № 102
ИЗМЕРЕНИЕ МОМЕНТА ИНЕРЦИИ.
ПРОВЕРКА ТЕОРЕМЫ ШТЕЙНЕРА
студента: ___________________________________ группы: _______
|
ДОПУСК |
ВЫПОЛНЕНИЕ |
||
|
дата |
подпись |
дата |
подпись |
|
|
|
|
|
1 Таганрог 2011
1. Изучаемое физическое явление:
Динамика вращательного движения твердого тела, момент силы, момент инерции, момент импульса материальной точки и твердого тела, основной закон динамики вращательного движения твердого тела.
2. Формулировка поставленной задачи:
Измерить момент инерции маховика и вкладыша. Проверить теорему Штейнера.
3. Таблица характеристик измерительных приборов:
|
Название прибора |
Диапазон измерений |
Число делений |
Класс точности |
Приборная погрешность |
Цена деления |
|
линейка |
|
|
|
|
|
|
секундомер |
|
|
|
|
|
4. Описание лабораторной установки и вывод расчетных формул.
Для измерения моментов инерции маховика и вкладыша, а также для проверки теоремы Штейнера используется экспериментальная установка, изображенная на рис. 1: при измерении времени ускоренного вращения маховика (рис. 1а) и при измерении времени замедленного вращения маховика (рис. 1б).
Экспериментальная установка состоит из массивного маховика 1, представляющего собой диск с восемью цилиндрическими отверстиями для вкладышей 2, расположенными симметрично оси маховика. Маховик насажен на вал 3, закрепленный горизонтально в подшипниках качения 4. В вале 3 маховика имеется отверстие, в которое вставляется штырь, прикрепленный к одному из концов нити 5. К другому концу нити 5 прикреплен крючок, на который подвешивается груз 6. Нить наматывается на вал 3 маховика и перебрасывается через легкий блок 7, который установлен на верхнем конце вертикальной стойки 8. Блок 7 можно поворачивать вокруг оси стойки с помощью поворотного устройства 9. В необходимое положение блок устанавливается рукоятками 10 и фиксируется прижимным винтом 11. На вертикальной стойке также закреплена линейка 12 для измерения перемещения груза при его движении. Перемещение груза отсчитывается от его нижнего основания в момент касания верхней точки клавиши выключателя В1 или В2. Время движения груза измеряется электронным секундомером. Включение и выключение секундомера осуществляется выключателями В1 и В2 соответственно. В исходном состоянии должны быть нажаты левая сторона клавиши выключателя В1 (контакты В1 разомкнуты) и правая сторона клавиши выключателя В2 (контакты В2 замкнуты).
В исходном состоянии груз 6 поднят на заданную высоту Н и удерживается в этом положении посредством внешнего воздействия на маховик. Если освободить маховик от внешнего воздействия, то система под действием сил, указанных на рис. 1, придет в движение.
Запишем второй закон Ньютона для опускающегося груза
![]() ,
,
где m
– масса груза;
![]() – ускорение груза;
– ускорение груза;
![]() – сила натяжения нити.
– сила натяжения нити.
В проекции на ось OZ (рис. 1) это уравнение имеет вид:
![]() .
(1)
.
(1)
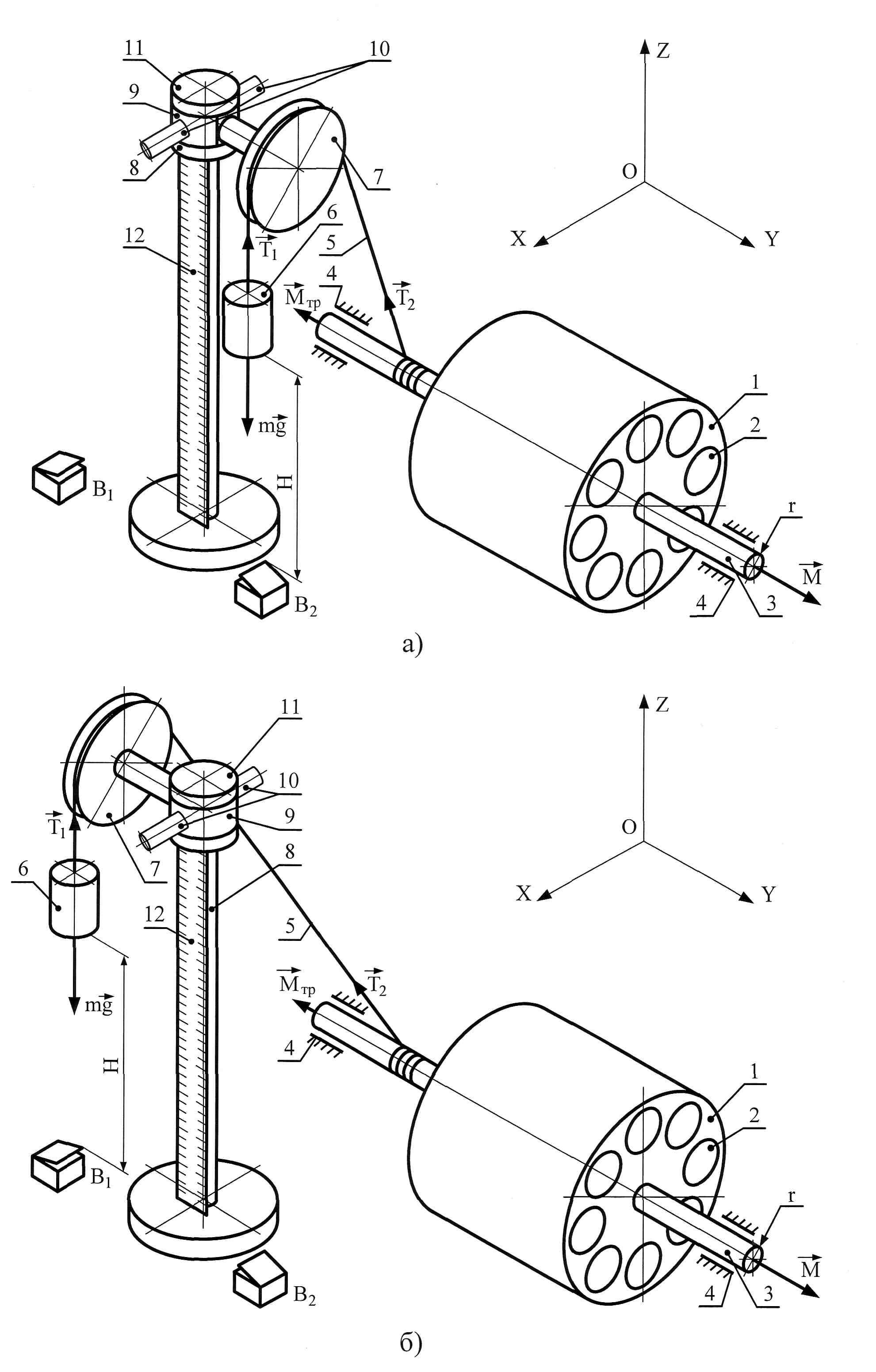
Рис. 1. Экспериментальная установка:
а) – при измерении времени ускоренного вращения маховика;
б) – при измерении времени замедленного вращения маховика
Запишем основной закон динамики вращательного движения для маховика
![]() ,
,
где ![]() – угловое ускорение маховика при
ускоренном движении;
– угловое ускорение маховика при
ускоренном движении;
![]() – вращающий момент силы T2;
– вращающий момент силы T2;
![]() – момент сил трения в подшипниках 4.
– момент сил трения в подшипниках 4.
В проекциях на ось OY (рис. 1)
![]() .
(2)
.
(2)
Здесь M и Mmp – моменты относительно оси маховика; направление вращающего момента M определяется правилом правого винта (M = T2r, r – радиус вала маховика); момент сил трения Mmp направлен в обратную сторону.
Пренебрегая массами блока 6, нити 5, а также трением в подшипниках оси блока, можно записать, что T1 = T2 = T. Тогда уравнения (1) и (2) примут вид
![]() ,
(3)
,
(3)
![]() .
(4)
.
(4)
Для нерастяжимой
нити величина ускорения
![]() груза будет равна касательному ускорению
точек поверхности вала маховика, т.е.
груза будет равна касательному ускорению
точек поверхности вала маховика, т.е.
![]() .
.
Учитывая, что
![]() и
и
![]() ,
получим
,
получим
![]() .
(5)
.
(5)
Решая совместно уравнения (3) – (5), получим
![]() .
(6)
.
(6)
Ускорение опускающегося груза можно определить, зная высоту H и время опускания груза t1, по соотношению
![]() .
(7)
.
(7)
Соотношение, связывающее искомую величину I с экспериментально определяемыми m, r, H и t1, получим из (6) с учетом (7):
![]() .
(8)
.
(8)
В экспериментальной установке длина нити подобрана так, что в момент касания грузом выключателя нить отделяется от вала маховика. С этого момента на маховик действует только момент сил трения в подшипниках вала. Поэтому уравнение движения маховика на основании основного закона динамики вращательного движения примет вид
![]() ,
(9)
,
(9)
где ε2 – угловое ускорение равнозамедленного движения маховика.
Поскольку конечная угловая скорость равноускоренного вращения маховика ω1 равна начальной угловой скорости его равнозамедленного вращения ω2 (ω1 = ω2), то, зная время равнозамедленного вращения t2, можно записать:
![]() ,
откуда
,
откуда
![]() .
(10)
.
(10)
Подставляя (10) в (9) с учетом (5) и (7), получим соотношение для Mmp:
![]() .
(11)
.
(11)
Из (8) и (11) получим расчетное соотношение для момента инерции маховика
![]() .
(12)
.
(12)
Величины m, r и H, входящие в расчетную формулу (12), являются параметрами экспериментальной установки и заданы в табл. 1, а t1 и t2 необходимо измерить опытным путем.
Поскольку момент инерции – величина аддитивная (момент инерции целого равен сумме моментов инерции отдельных частей), то момент инерции маховика с вкладышами относительно оси вращения маховика равен
![]() ,
(13)
,
(13)
где In – момент инерции маховика с n вкладышами относительно оси вращения маховика;
I0 – момент инерции маховика без вкладышей относительно оси вращения маховика;
Iв – момент инерции одного вкладыша относительно оси вращения маховика;
n – число вкладышей (n ≤ 8).
Таким образом, экспериментальное значение момента инерции одного
вкладыша Iв относительно оси вращения маховика можно определить по результатам экспериментальных измерений In и I0 по формуле
![]() .
(14)
.
(14)
Вкладыш маховика является прямым круговым цилиндром. Это позволяет непосредственно по радиусу вкладыша rв, массе вкладыша mв, а также расстоянию
|
Рис. 2. |
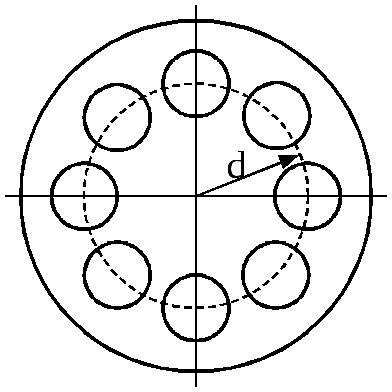
между осью вращения маховика и осью симметрии вкладыша d (см. рис. 2) рассчитать теоретическое значение момента инерции одного вкладыша относительно оси вращения маховика Iвт по теореме Штейнера. Согласно теореме Штейнера момент инерции тела относительно любой оси равен сумме момента инерции этого тела относительно оси, параллельной данной, но проходящей через центр масс, и произведения массы тела на квадрат расстояния между осями
где Iв0 – момент инерции вкладыша маховика относи- |
тельно оси симметрии вкладыша, который равен
![]() .
.
С учетом последнего соотношения получим окончательную формулу для рас-
чета теоретического значения момента инерции одного вкладыша относительно оси вращения маховика
![]() .
(16)
.
(16)
Для проверки справедливости теоремы Штейнера необходимо:
1) по экспериментально измеренному моменту инерции маховика без вкладышей I0 и моменту инерции маховика с вкладышами In вычислить экспериментальное значение момента инерции одного вкладыша относительно оси вращения маховика Iв по формуле (14);
2) вычислить теоретическое значение момента инерции одного вкладыша относительно оси вращения маховика IвТ по формуле (16);
3) сравнить полученные экспериментальное и теоретическое значения моментов инерции вкладыша маховика между собой.