5. Аналитические функции

Определение 5.7. Функция f(z) называется аналитической в точке, если она дифференцируема в некоторой окрестности этой точки.

Определение 5.8. Функция f(z) называется аналитической в области Ω, если она дифференцируема в каждой ее точке, а ее производная непрерывна в этой области.

Замечание. Условие непрерывности производной аналитической функции в дальнейшем можно будет снять, поскольку аналитическая функция комплексной переменной оказывается бесконечно дифференцируемой (см. ниже свойство 5.6).

Из теоремы 4.1 и из условий дифференцируемости функций двух переменных вытекает следующий критерий аналитичности: Для аналитичности функции f(z) = u(x,y) + i v(x,y) в области Ω необходимо и достаточно, чтобы в этой области существовали непрерывные частные производные функций u(x,y) и v(x,y), удовлетворяющие условиям Коши – Римана (4.1).

1. Свойства аналитических функций

Ряд свойств дифференцируемых функций действительного переменного легко переносится на аналитические функции из - за идентичности определения производных. Но имеются и ряд специфических свойств (см. далее свойства 3,4,5).

Свойство 5.1. (об арифметических действиях над аналитическими функциями). Если f₁(z) и f₂(z) аналитические в области Ω, то их сумма, разность, и произведение являются аналитическими функциями. Функция является аналитической всюду в области Ω, где f₂(z)  0.

Свойство 5.2. (об аналитичности суперпозиции). Если w = f(z) аналитическая функция в области Ω(z) комплексной плоскости, а в области ее значений Ω(w) определена аналитическая функция  = (w), то функция F(z) = (f(z)), является аналитической в области Ω(z).

Свойство 5.3. (об аналитичности обратной функции). Пусть w = f(z) аналитическая функция в области Ω(z), причем. Тогда в области ее значений Ω(w) определена обратная функция z = f ^– 1(w), являющаяся аналитической функцией в области Ω(w) и имеет место равенство.

С

Рис. 3. Пути интегрирования при вычислении криволинейного интеграла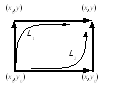

войство 5.4. (о восстановлении аналитической функции). Действительная (мнимая) части аналитической функции в некоторой области восстанавливаются с точностью до аддитивной константы по известной мнимой (действительной) части этой функции.

Доказательство. Пусть, например, известна действительная часть u(x,y) аналитической функции f(z) = u(x,y) + i v(x,y). Условия Коши – Римана (5.1) позволяют найти полный дифференциал неизвестной мнимой части: . Остается воспользоваться правилом восстановления функции по ее полному дифференциалу

,

которое определит функцию v(x,y) c точностью до константы. При вычислении криволинейного интеграла, учитывая, что подынтегральное выражение является полным дифференциалом и не зависит от пути интегрирования, выбран путь L₁ , показанный на рис.3. Аналогично можно получить формулу для восстановления действительной части аналитической функции:

Доказательство закончено.

Определение 5.9. Две линии называются ортогональными в точке пересечения, если ортогональны их касательные в этой точке.

Свойство 5.5. Пусть f(z) = u(x,y) + i v(x,y) аналитическая функция в области Ω. Семейства линий уровня действительной и мнимой части u(x,y) = C₁, v(x,y) = C₂ взаимно ортогональны:

(grad u, grad v) = 0.

Доказательство вытекает из условий Коши - Римана (5.1):

Свойство 5.6. Функция f(z), аналитическая в области Ω имеет в каждой точке этой области производные любого порядка.

Доказательство, основанное на представлении аналитических функций рядами Тейлора, мы опускаем. Отметим в этой связи, что возможность представления функции степенным рядом равносильна аналитичности и во многих учебниках такие функции по определению называются аналитическими (см, например книги [3, 4, 5]). Отметим также, что существование производных любого порядка от аналитической функции вытекает из формулы Коши, которая будет доказана в дальнейшем.