
- •Оглавление
- •Часть 1. Основы теории функций комплексной
- •Часть 2. Решение задач по теории функций
- •Предисловие
- •Часть 1. Основы теории функций комплексной переменной
- •Алгебра комплексных чисел
- •Различные формы представления комплексных чисел
- •Предел последовательности комплексных чисел
- •Расширение понятия комплексная плоскость
- •Сфера Римана
- •Функции комплексной переменной (фкп)
- •Степенные функции
- •Показательная функция
- •Тригонометрические функции
- •Гиперболические функции
- •Логарифмическая функция
- •Обратные тригонометрические функции
- •Предел, непрерывность, дифференцируемость
- •Аналитические функции
- •Свойства аналитических функций
- •Интеграл по комплексной переменной.
- •Основные свойства.
- •Теорема Коши
- •Неопределенный интеграл и формула Ньютона - Лейбница
- •Формула Коши
- •Представление аналитических функций степенными рядами
- •Ряды Тейлора.
- •Ряд Лорана.
- •Особые точки аналитической функции.
- •Классификация особых точек
- •Теоремы о вычетах
- •Об аналитическом продолжении
- •Вычисление интегралов типа
- •Вычисление интегралов типа
- •Леммы Жордано
- •Вычисление несобственных интегралов.
- •Интегралы типа
- •Контур Бромвича и интеграл Бромвича – Вагнера.
- •Функция Хевисайда и ее интегральные представления
- •Часть 2. Решение задач по теории функций комплексной переменной
- •Комплексные числа
- •Формы записи комплексных чисел
- •Примеры с решениями
- •Алгебраические операции над комплексными числами
- •Задачи для самостоятельного решения
- •Элементарные функции комплексного переменного
- •Представление элементарных функций комплексного переменного в алгебраической форме
- •Задачи для самостоятельного решения
- •Аналитические функции комплексного переменного
- •Дифференцируемость и аналитичность функций комплексного переменного.
- •Примеры с решениями
- •Задачи для самостоятельного решения
- •Интегрирование функций комплексного переменного
- •Вычисление интегралов. Теорема Коши. Интегральная формула Коши
- •Примеры с решениями
- •Задачи для самостоятельного решения.
- •Вычеты. Контурные интегралы
- •Классификация особых точек.
- •Примеры с решениями.
- •Вычеты. Вычисление контурных интегралов
- •Примеры с решениями
- •Задачи для самостоятельного решения
- •Вычисление определенных интегралов от действительных функций
- •Интегралы типа
- •Вычисление несобственных интегралов второго рода
- •Вычисление интегралов вида
- •Задачи для самостоятельного решения
- •Библиографический список
- •394000, Воронеж, пр. Революции, 19
Часть 1. Основы теории функций комплексной переменной
Введение
История появления комплексных чисел начинается с попыток найти всевозможные корни квадратного уравнения, но наибольший интерес к ним возник в связи с проблемами интегрирования рациональных функций: возможно ли представление любого многочлена с действительными коэффициентами в виде произведений линейных и квадратичных выражений также с действительными коэффициентами. Лейбниц утверждал, что это не так (1702 год, переписка с И. Бернулли, см. [1]) и в качестве подтверждения приводил пример разложения на множители
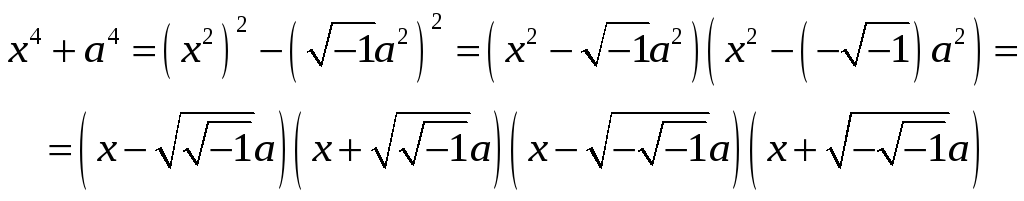
утверждая, что никакая пара из найденных четырех множителей не может дать в произведении многочлен с действительными коэффициентами.
Однако, как нетрудно убедиться, заключение
Лейбница ложно, поскольку![]() .
Поэтому проблема заключается в
интерпретации выражений вида
.
Поэтому проблема заключается в
интерпретации выражений вида![]() .
Развитие теории комплексных величин
дало ответ на этот вопрос.
.
Развитие теории комплексных величин
дало ответ на этот вопрос.
Длительный срок становления теории
комплексных чисел (почти сто лет) связан
с путаницей, которую вносили в
математические рассуждения два хорошо
известных алгебраических правила:![]() ,
,
![]()
![]() ,
справедливые для действительных чисел.
Эти правила позволяют трактовать
,
справедливые для действительных чисел.
Эти правила позволяют трактовать
![]() по-разному:
по-разному:
![]() или
или![]() .
.
Лишь с середины восемнадцатого века в
теории комплексных чисел наступает
(современный) порядок, с введением в
теорию в качестве аксиомы утверждения
![]() (Л.Эйлер). Интересно отметить, что в 1702
году отношение к комплексным числам
мировой научной мысли было (сформулировано
Лейбницем) как к «уродам из мира идей».
Но в тридцатых годах восемнадцатого
века комплексные числа прочно вошли в
обиход передовых научных исследований,
и к этому времени Эйлер практически
завершил создание теории элементарных
функций комплексного переменного
(«Введение в анализ бесконечно малых»,
1748 год).
(Л.Эйлер). Интересно отметить, что в 1702
году отношение к комплексным числам
мировой научной мысли было (сформулировано
Лейбницем) как к «уродам из мира идей».
Но в тридцатых годах восемнадцатого
века комплексные числа прочно вошли в
обиход передовых научных исследований,
и к этому времени Эйлер практически
завершил создание теории элементарных
функций комплексного переменного
(«Введение в анализ бесконечно малых»,
1748 год).
-
Алгебра комплексных чисел
Комплексным числом называется число
z = x + iy, где x
и y – действительные числа, и по
определению положено![]() .
Число x называется действительной
частью комплексного числа z,
обозначается Re z, а число y
называется мнимой частью числа z,
обозначается Im z. При этом два
комплексных числа z1 = x1 + iy1
и z2 = x2 + iy2
считаются равными, если x1 = x2
и y1 = y2. Следует
отметить необычную роль, которую играет
знак « + » в определении комплексного
числа. Этот знак разделяет x и y,
и мог быть заменен, например, запятой,
то есть комплексное число можно
рассматривать как упорядоченную пару
(x,y) действительных чисел (старое
русское название комплексного числа -
«комплект»). На множестве комплексных
чисел алгебраические операции сложения
и умножения определяются как для
многочленов (двучленов):
.
Число x называется действительной
частью комплексного числа z,
обозначается Re z, а число y
называется мнимой частью числа z,
обозначается Im z. При этом два
комплексных числа z1 = x1 + iy1
и z2 = x2 + iy2
считаются равными, если x1 = x2
и y1 = y2. Следует
отметить необычную роль, которую играет
знак « + » в определении комплексного
числа. Этот знак разделяет x и y,
и мог быть заменен, например, запятой,
то есть комплексное число можно
рассматривать как упорядоченную пару
(x,y) действительных чисел (старое
русское название комплексного числа -
«комплект»). На множестве комплексных
чисел алгебраические операции сложения
и умножения определяются как для
многочленов (двучленов):
z1 + z2 = x1 + x2 + i(y1 + y2 ), z1 z2 = x1 x2 – y1 y2 + i(x1 y2 + x2 y1).
Роль комплексного нуля выполняет число
0 = 0 + i0 а роль комплексной
единицы число 1 = 1 + i0. При
этом очевидно, что для каждого элемента
z противоположным элементом является
комплексное число – z:
z + ( – z) = 0. Легко
проверяется, что в случае, если z
0 обратный элемент z – 1
(т.е. такой, что z · z – 1 = 1)
единственным образом определяется по
формуле![]() ,
где
,
где![]() .
При этом действительное число
.
При этом действительное число
![]() называется модулем комплексного числа
z, а комплексные числа z и
называется модулем комплексного числа
z, а комплексные числа z и![]() –
комплексно сопряженными друг к другу.
Комплексное число можно рассматривать
как расширение понятия действительного
числа. Множество действительных чисел
1 можно
рассматривать как подмножество множества
комплексных чисел, которое обозначается
символом .
–
комплексно сопряженными друг к другу.
Комплексное число можно рассматривать
как расширение понятия действительного
числа. Множество действительных чисел
1 можно
рассматривать как подмножество множества
комплексных чисел, которое обозначается
символом .
При этом для комплексных чисел выполняются все основные законы справедливые для действительных чисел за исключением упорядоченности, то есть понятия «больше», «меньше» неприменимы к комплексным числам.
