
- •Оглавление
- •Часть 1. Основы теории функций комплексной
- •Часть 2. Решение задач по теории функций
- •Предисловие
- •Часть 1. Основы теории функций комплексной переменной
- •Алгебра комплексных чисел
- •Различные формы представления комплексных чисел
- •Предел последовательности комплексных чисел
- •Расширение понятия комплексная плоскость
- •Сфера Римана
- •Функции комплексной переменной (фкп)
- •Степенные функции
- •Показательная функция
- •Тригонометрические функции
- •Гиперболические функции
- •Логарифмическая функция
- •Обратные тригонометрические функции
- •Предел, непрерывность, дифференцируемость
- •Аналитические функции
- •Свойства аналитических функций
- •Интеграл по комплексной переменной.
- •Основные свойства.
- •Теорема Коши
- •Неопределенный интеграл и формула Ньютона - Лейбница
- •Формула Коши
- •Представление аналитических функций степенными рядами
- •Ряды Тейлора.
- •Ряд Лорана.
- •Особые точки аналитической функции.
- •Классификация особых точек
- •Теоремы о вычетах
- •Об аналитическом продолжении
- •Вычисление интегралов типа
- •Вычисление интегралов типа
- •Леммы Жордано
- •Вычисление несобственных интегралов.
- •Интегралы типа
- •Контур Бромвича и интеграл Бромвича – Вагнера.
- •Функция Хевисайда и ее интегральные представления
- •Часть 2. Решение задач по теории функций комплексной переменной
- •Комплексные числа
- •Формы записи комплексных чисел
- •Примеры с решениями
- •Алгебраические операции над комплексными числами
- •Задачи для самостоятельного решения
- •Элементарные функции комплексного переменного
- •Представление элементарных функций комплексного переменного в алгебраической форме
- •Задачи для самостоятельного решения
- •Аналитические функции комплексного переменного
- •Дифференцируемость и аналитичность функций комплексного переменного.
- •Примеры с решениями
- •Задачи для самостоятельного решения
- •Интегрирование функций комплексного переменного
- •Вычисление интегралов. Теорема Коши. Интегральная формула Коши
- •Примеры с решениями
- •Задачи для самостоятельного решения.
- •Вычеты. Контурные интегралы
- •Классификация особых точек.
- •Примеры с решениями.
- •Вычеты. Вычисление контурных интегралов
- •Примеры с решениями
- •Задачи для самостоятельного решения
- •Вычисление определенных интегралов от действительных функций
- •Интегралы типа
- •Вычисление несобственных интегралов второго рода
- •Вычисление интегралов вида
- •Задачи для самостоятельного решения
- •Библиографический список
- •394000, Воронеж, пр. Революции, 19
-
Формула Коши
Теорема 9.8.
Пусть функция f(z) аналитична в
замкнутой области
![]() и z0 Ω –
произвольная точка. Тогда имеет место
формула Коши
и z0 Ω –
произвольная точка. Тогда имеет место
формула Коши
![]() ,
(9.1)
,
(9.1)
где C – произвольный замкнутый
контур, целиком лежащий в
![]() и содержащий точку z0 внутри
себя.
и содержащий точку z0 внутри
себя.
Доказательство. Пусть ε – произвольное достаточно малое число, такое, что окружность этого радиуса с центром в точке z0 целиком лежит внутри контура C. Подынтегральная функция аналитична в области |z – z0| < ε. Поэтому можно применить следствие теоремы 7.3. Таким образом

 .
.
Используя очевидное равенство![]() ,
получим
,
получим
![]()
![]() ,
где
максимум берется по всем
,
где
максимум берется по всем![]() .
.
Левая часть этого неравенства не зависит от ε, правая же часть может быть произвольно мала при малом ε (ввиду непрерывности f(z)). Такая ситуация возможна лишь в случае когда левая часть равна нулю. Доказательство закончено.
Следствие 1. При выполнении условий теоремы 9.1 аналитическая функция имеет производные любого порядка и
![]() . (9.2)
. (9.2)
Доказательство. Предполагая, точку z0 переменной и продифференцировав равенство (9.1) n раз по z0, получим (9.2). О возможности дифференцирования по параметру под знаком интеграла смотрите в [3], стр. 51 – 52.
Пример 9.1.
Вычислить интеграл![]() ,
если С – окружность a) |z| = 1,
b) |z| = 3. Ответ: a) 0; b)
2π i e2.
,
если С – окружность a) |z| = 1,
b) |z| = 3. Ответ: a) 0; b)
2π i e2.
Рассмотрим случай, когда точка
![]() лежит на контуре (см. рис. 7). Покажем, что
в этом случае
лежит на контуре (см. рис. 7). Покажем, что
в этом случае![]() .
Будем рассматривать далее контур C
как разорванный в точке
.
Будем рассматривать далее контур C
как разорванный в точке![]() .
Сразу заметим, что интегралы по дугам
полуокружностей
.
Сразу заметим, что интегралы по дугам
полуокружностей![]() ,
,
![]() вычисляются аналогично интегралу в
доказательстве теоремы 9.1.
вычисляются аналогично интегралу в
доказательстве теоремы 9.1.
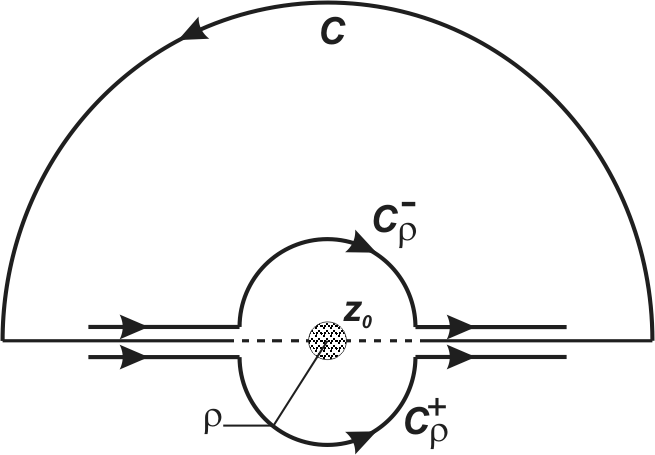
Рис. 7. Варианты обхода полюса.
Соответственно ,
,
 .
Рассмотрим интеграл по замкнутому
контуру
.
Рассмотрим интеграл по замкнутому
контуру![]() (
(![]() -
большая полуокружность в верхней
полуплоскости). В области, ограниченной
контуром подынтегральная функция не
содержит особых точек. Поэтому интеграл
по контуру равен нулю. С другой стороны,
-
большая полуокружность в верхней
полуплоскости). В области, ограниченной
контуром подынтегральная функция не
содержит особых точек. Поэтому интеграл
по контуру равен нулю. С другой стороны,
 .
.
При обходе особой точки снизу получим
 .
.
Как видим, любой вариант обхода приводит к одному и тому же результату для исследуемого интеграла. Следовательно, формулу Коши можно записать следующим образом
 (9.3)
(9.3)
-
Представление аналитических функций степенными рядами
-
Ряды Тейлора.
-
Представление функции в окрестности некоторой точки z0 в виде степенного ряда во многих учебниках по ТФКП служит определением аналитической функции. Из следующей теоремы, которую мы приведем без доказательства, и второй теоремы Абеля (об абсолютной сходимости степенного ряда внутри круга сходимости, см.[2], стр. 621) вытекает равносильность таких определений аналитичности.
Теорема 10.9
(Теорема Вейерштрасса) Пусть члены ряда
![]() являются аналитическими функциями в
некоторой области Ω, а сам ряд сходится
равномерно к функции f(z) в каждой
замкнутой подобласти Ω' области Ω. Тогда:
являются аналитическими функциями в
некоторой области Ω, а сам ряд сходится
равномерно к функции f(z) в каждой
замкнутой подобласти Ω' области Ω. Тогда:
1) f(z) является аналитической функцией в области Ω.
2)![]() .
.
3) Ряд
![]() сходится равномерно в любой замкнутой
подобласти Ω' области Ω.
сходится равномерно в любой замкнутой
подобласти Ω' области Ω.
Доказательство этого утверждения см. в [3], стр.61.
Теорема 10.10
(теорема Тейлора). Функция f(z),
аналитическая внутри круга |z – z0| <
R, может быть представлена в этом
круге сходящимся степенным рядом![]() ,
причем этот ряд определен однозначно.
,
причем этот ряд определен однозначно.
Доказательство. Выберем произвольную
точку z внутри круга
![]() и построим окружность Cρ
радиуса ρ
и построим окружность Cρ
радиуса ρ
![]() с центром в точке z0.
По формуле Коши имеем
с центром в точке z0.
По формуле Коши имеем
 .
.
Из теории рядов нам известно разложение![]() ,
которое справедливо в области |q| < 1.
Очевидно, что
,
которое справедливо в области |q| < 1.
Очевидно, что![]() .
Поэтому
.
Поэтому
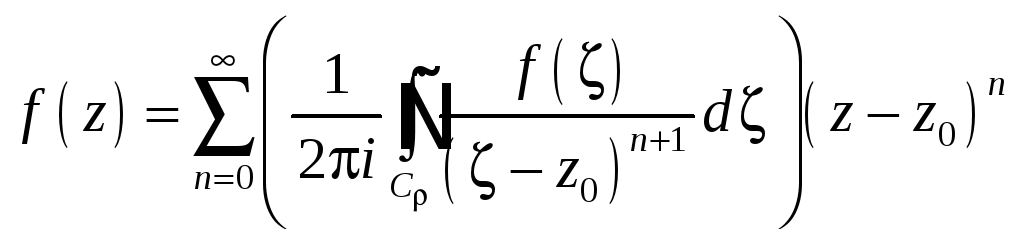 .
.
Теперь формула (9.2) дает нам ряд
![]() ,
,
![]() , (10.1)
, (10.1)
который, как нам уже известно, называется рядом Тейлора функции f(z). Единственность представления функции ее рядом Тейлора достаточно просто вытекает из единственности представления коэффициентов Тейлора (10.1). Доказательство закончено.
Замечание 10.1. f(z) – функция
аналитическая в точке z0 , если
( D > 0 )
( z{|z – z0| < D} )
![]()
