1.5. Компланарные векторы

Определение 7. Векторы называются компланарными, если их можно отложить в одной плоскости.

Свойства компланарных векторов.

1⁰. Коллинеарные векторы компланарны. Иными словами, во множество всех возможных компланарных между собой векторов вместе с каждым его вектором входят все векторы, коллинеарные с ним. В частности, нулевой вектор содержится в любом таком множестве и вместе с каждым вектором в это множество входит противоположный ему вектор. Отсюда же следует, что множество компланарных векторов замкнуто относительно операции умножения на действительное число.

2⁰. Сумма двух векторов есть вектор, компланарный с ними. Следовательно, множество компланарных векторов замкнуто относительно операции сложения.

3⁰. Три вектора компланарны тогда и только тогда, когда хотя бы один из них можно представить в виде линейной комбинации двух других.

Доказательство.  Пусть векторы компланарны. Возможны два случая.

1) Среди данных векторов есть хотя бы одна пара коллинеарных векторов. Пусть и коллинеарны. Тогда, по свойствам коллинеарных векторов, хотя бы один из них можно выразить через другой. Пусть . Тогда , т.е. вектор есть линейная комбинация векторов и .

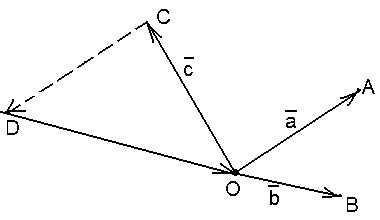
2) Данные векторы попарно не коллинеарны. Отложим их от одной точки О. Пусть , , . Отрезки ОА, ОВ, ОС попарно не параллельны. Проведём СD ОА так, что D  ОВ (прямой ОВ). Тогда , т.е. вектор есть линейная комбинация векторов и .

Рис. 7

 Пусть . По свойствам 1⁰ и 2⁰ следует, что вектор компланарен с векторами и .

4⁰. Если векторы и не коллинеарны, то любой компланарный с ними вектор можно представить в виде их линейной комбинации.

5⁰. Из свойств 1⁰ и 2⁰ следует, что множество всех возможных компланарных векторов относительно операций сложения векторов и умножения вектора на действительное число ведёт себя так же, как множество всех коллинеарных векторов и как множество всех геометрических векторов. Кроме того, для задания множества всех возможных компланарных векторов достаточно задать любые два не коллинеарные из них.

Задача 3.

1.6. Векторные пространства

Определение 8. Множество векторов V называется векторным пространством, если в нём определены две алгебраические операции: сложение векторов и умножение вектора на действительное число, удовлетворяющие следующим требованиям:

1. Множество V замкнуто относительно обеих операций.

2. для любых векторов и (коммутативный закон сложения).