З.И.Андреева
Аналитическая геометрия
(для направления «Прикладная математика и информатика»)
Содержание
Введение
I. Элементы векторной алгебры ……………………………………………………
1.1. Определение и свойства векторов ………………………………………………………..
1.2. Сложение векторов …………………………………………………………………………..
1.3. Умножение вектора на действительное число …………………………………………
1.4. Коллинеарные векторы ……………………………………………………………………….
1.5. Компланарные векторы ………………………………………………………………………
I. Элементы векторной алгебры
1.1. Определение и свойства векторов
Определение 1. Геометрический отрезок называется ориентированным, если указан порядок его концов.
Определение 2. Вектором (геометрическим вектором) называется ориентированный отрезок. При этом начало и конец ориентированного отрезка называются соответственно началом и концом вектора. Длина ориентированного отрезка называется длиной вектора.
Вектор обозначается
,
где А – начало, а В – конец вектора.
Если начало и конец вектора нас не
интересуют, то вектор обозначают
.
Длина вектора обозначается
или
.
Если начало и конец вектора совпадают,
то вектор называют нулевым и
обозначают
.
Если начало и конец вектора – различные
точки (А В), то
существует и только один луч с началом
А, проходящий через точку В. Этот луч
задаёт в пространстве направление,
которое называется направлением
данного вектора. Нулевой вектор не
имеет направления.
Определение 3. Два вектора называются равными, если они либо оба нулевые, либо имеют одинаковые длину и направление.
Равенство векторов обладает
следующими очевидными свойствами: 1)
рефлексивность (всякий вектор
равен сам себе); 2) симметричность
( если
,
то
);
3) транзитивность
(если
и
,
то
).
Множество всех равных векторов можно задать 1) одним из векторов (ориентированным отрезком); 2) упорядоченной парой точек; 3) длиной и направлением (в случае ненулевого вектора).
|
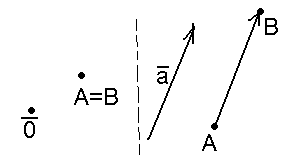
Пусть
даны вектор
|
Рис. 1 |
и точка А. Если
,
то существует и только один вектор с
началом в точке А, равный данному
вектору. Это вектор
(т.е. В = А). Если
,
то существует и только один луч,
сонаправленный с вектором
.
На этом луче существует и только одна
точка В, расстояние от которой до точки
А равно
.
Но тогда
(рис. 1). Будем говорить, что вектор
отложен от точки А. Итак, любой вектор
можно отложить от любой точки и только
единственным образом.
1.2. Сложение векторов
|
Пусть
А (
Свойства сложения векторов. |
Рис. 2 |
и
любые два вектора.
Чтобы к вектору
прибавить вектор
нужно
отложить вектор
от любой точки
),
от конца В полученного вектора отложить
вектор
(
).
Тогда вектор
будет вектором суммы, т.е.
.
Иными словами,
.
10. Для любых двух векторов их сумма определена и однозначна. (Следует из определения).
20.
=
для любого вектора
.
(Докажите).
30. Для любого вектора
существует противоположный вектор
(
)
такой, что
+
(
)
=
.
(Докажите).
40.
для любых векторов
и
.
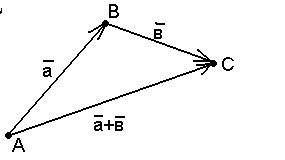
Доказательство. В случае, когда хотя бы один из векторов нулевой, утверждение следует из предыдущего свойства. Остаётся рассмотреть ненулевые векторы. При этом возможны следующие случаи.
|
а) Векторы
Отложим от точки А вектор
|
Рис. 3 |
и
не параллельны. Пусть
+
=
.
,
пусть
.
Так как
и
имеют одинаковые длины и направления,
то АВСD – параллелограмм.
Следовательно, отрезки АВ и DC
тоже имеют одинаковые длины и
направления. Следовательно,
.
По правилу сложения векторов
и
.
Отсюда
.
|
б) Векторы
|
Рис. 4 |
и
параллельны и одинаково направлены
(сонаправлены). В этом случае при
откладывании от точки А получим
,
(рис.4). Векторы
и
сонаправлены с вектором
,
поэтому сонаправлены между собой.
Очевидно,
.
Следовательно,
,
т.е.
.
в) Случай, когда векторы
и
параллельны и противоположно направлены,
рассмотрите самостоятельно.
Определение 4. Векторы называются коллинеарными, если их можно отложить на одной прямой.
Очевидно, два вектора неколлинеарны тогда и только тогда, когда они ненулевые и не параллельные. Из случая а) проведённого доказательства следует ещё одно правило сложения неколлинеарных векторов:
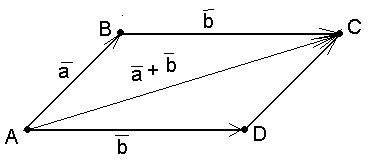
Чтобы сложить два неколлинеарных вектора, достаточно отложить их от одной точки, построить на них, как на сторонах, параллелограмм, тогда диагональ этого параллелограмма, идущая из данной точки, будет задавать вектор суммы.
|
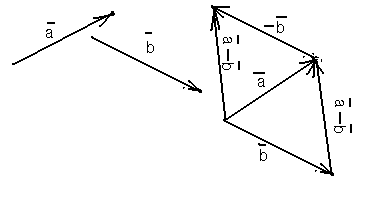
50.
Доказательство. Для левой части получим
|
Рис. 5 |
для любых векторов
.
Для правой части
.
Результаты равны.
Определение 5. Разностью упорядоченной пары векторов называется сумма первого вектора и вектора, противоположного второму, т.е.
.
|
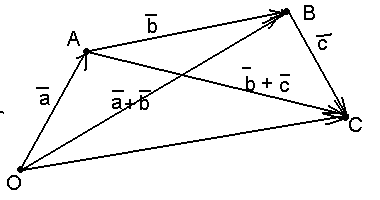
Чтобы вычесть из одного вектора второй, достаточно отложить оба вектора от одной точки. Тогда вектор, соединяющий концы полученных отрезков и направленный в сторону уменьшаемого, будет вектором разности (рис. 5). Очевидно, это правило не зависит от того, будут ли векторы коллинеарными или неколлинеарными. Свойства разности: |
Рис. 6 |
10. Для любой упорядоченной пары векторов их разность определена и однозначна.
20. Разность двух векторов антикоммутативна.
для любых векторов
и
.
30. Не выполняется ассоциативный закон, а именно
для любых векторов
,
и
.
40. Выполняются дистрибутивные законы:
и
для любых векторов
,
и любых действительных чисел ,
.
Задача 1.
