
- •Оглавление
- •Глава I. Алгебра матриц
- •1.1. Матрицы. Основные определения
- •1.2. Действия над матрицами
- •1.3. Задания для самостоятельной работы по главе 1
- •Глава 2. Определители
- •2.1. Перестановки и подстановки
- •2.2. Определители и их свойства
- •2.3. Миноры и алгебраические дополнения
- •2.4. Вычисление определителей n-го порядка
- •2.5. Задания для самостоятельной работы по главе 2
- •Глава 3. Алгебра матриц (продолжение)
- •3.1. Обратная матрица
- •3.2. Ранг матрицы
- •3.3. Линейная зависимость и независимость строк матрицы
- •3.4. Многочленные матрицы
- •3.5. Задания для самостоятельной работы по главе 3
- •Глава 4. Решение системы линейных уравнений
- •4.1. Система линейных уравнений
- •4.2. Методы решения системы n линейных уравнений с n неизвестными
- •4.3. Теорема Кронекера-Капелли
- •4.4. Метод Жордана-Гаусса
- •4.5. Однородные системы линейных уравнений
- •4.6. Задания для самостоятельной работы по главе 4
- •Глава 5. Векторные пространства
- •5.1. Понятие векторного пространства
- •5.2. Линейная зависимость и независимость векторов
- •5.3. Базис векторного пространства
- •5.4. Изоморфизм векторных пространств
- •5.5. Преобразование координат при изменении базиса
- •5.6. Евклидово пространство
- •5.7. Ортогональные преобразования
- •5.8. Выпуклые множества
- •5.9. Задания для самостоятельной работы по главе 5
- •Глава 6. Линейные операторы
- •6.1. Определение линейного оператора
- •6.2. Характеристический многочлен и характеристическое уравнение
- •6.3. Собственный вектор и собственное число линейного оператора
- •6.4. Задания для самостоятельной работы по главе 6
- •Глава 7. Квадратичные формы
- •7.1. Определение квадратичной формы
- •7.2. Линейное преобразование переменных в квадратичной форме
- •7.3. Ортогональное преобразование квадратичной формы к каноническому виду
- •7.4. Положительно определенные квадратичные формы
- •7.5. Задания для самостоятельной работы по главе 7
- •Глава 8. Элементы общей алгебры
- •8.1. Алгебраические операции
- •8.2. Полугруппы и моноиды
- •8.3. Группы: определение и примеры
- •8.4. Циклические группы. Группы подстановок
- •8.5. Кольца: определение, свойства, примеры
- •8.6. Поле
- •8.7. Задания для самостоятельной работы по главе 8
- •Глава 9. Элементы теории чисел
- •9.1. Наибольший общий делитель
- •9.2. Наименьшее общее кратное
- •9.3. Простые числа
- •9.4. Сравнения и классы вычетов
- •9.5. Функция Эйлера
- •9.6. Функция Мебиуса
- •9.7. Задания для самостоятельной работы по главе 9
- •Список литературы
1.2. Действия над матрицами
Две
матрицы
![]() и
и
![]()
![]() называются равными, А=В, если их
соответствующие элементы равны, т.е.
называются равными, А=В, если их
соответствующие элементы равны, т.е.
![]() =
=![]() ,
,![]()
Суммой
двух матриц
![]() и
и
![]() называется матрица C=A+B,
элементы которой сij
равны сумме соответствующих элементов
aij
и bij
матриц A и B, т.е.
называется матрица C=A+B,
элементы которой сij
равны сумме соответствующих элементов
aij
и bij
матриц A и B, т.е.
![]() .
Например,
.
Например,
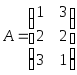 ,
,
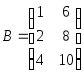 ,
,
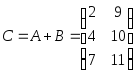 .
.
Для суммы матриц справедливы следующие свойства:
-
A+B=B+A – коммутативность;
-
A+(B+C)=(A+B)+C – ассоциативность;
-
A+О=A.
Произведением
матрицы
![]() на число
на число
![]() называется матрица
называется матрица
![]() ,
элементы которой равны произведению
соответствующих элементов матрицы A на
число
,
элементы которой равны произведению
соответствующих элементов матрицы A на
число
![]() ,
т.е.
,
т.е.
![]() .
Например, если
.
Например, если
![]() ,
а матрица
,
а матрица
![]() ,
то
,
то
![]() .
.
Пусть
A, B, C – матрицы,
![]() – числа. Из определения произведения
матрицы на число вытекают следующие
свойства:
– числа. Из определения произведения
матрицы на число вытекают следующие
свойства:
1.
![]() , 4.
, 4.
![]() ,
,
2.
![]() , 5.
, 5.
![]() ,
,
3.
![]() О, 6.
О, 6.
![]() .
.
Матрица
![]() называется
противоположной матрице A.
называется
противоположной матрице A.
Если
матрицы A и B одинаковых размеров, то их
разность равна
![]() .
.
Произведением
матрицы
![]() порядка
порядка
![]() на матрицу
на матрицу
![]() порядка
порядка
![]() называется матрица
называется матрица
![]() порядка
порядка
![]() ,
элементы которой с
,
элементы которой с![]() равны:
равны:
![]() ,
(
,
(![]() ;
;
![]() ).
).
Из определения произведения матриц следует: чтобы получить элемент, стоящий на пересечении i-ой строки и j-го столбца матрицы С, необходимо элементы i-ой строки матрицы А умножить на соответствующие элементы j-го столбца матрицы В и полученные произведения сложить.
Произведение АВ имеет смысл тогда и только тогда, когда число столбцов матрицы А равно числу строк матрицы В.
В результате получится матрица, у которой число строк совпадает с числом строк первого сомножителя, а число столбцов – с числом столбцов второго сомножителя.
Для произведения матриц справедливы следующие свойства:
|
1. A(BC) = (AB)C |
3. (A + B)C = AC + BC |
|
2.
|
4. C(A+B) = CA + CB |
Эти свойства легко доказываются на основе соответствующих определений.
Произведение
двух матриц некоммутативно, т.е. в общем
случае АВ![]() ВА.
В случае прямоугольных матриц легко
подобрать примеры, когда одно из этих
произведений не будет существовать
из-за невыполнения условия равенства
числа столбцов сомножителя, стоящего
первым, числу строк второго сомножителя.
Очевидно, что для квадратных матриц
порядка n
существуют АВ и ВА. Однако для всех n,
начиная с n=2,
можно привести примеры некоммутативных
(неперестановочных) матриц.
ВА.
В случае прямоугольных матриц легко
подобрать примеры, когда одно из этих
произведений не будет существовать
из-за невыполнения условия равенства
числа столбцов сомножителя, стоящего
первым, числу строк второго сомножителя.
Очевидно, что для квадратных матриц
порядка n
существуют АВ и ВА. Однако для всех n,
начиная с n=2,
можно привести примеры некоммутативных
(неперестановочных) матриц.
Пример. Найти произведение АВ и ВА матриц:
А
=
![]() ,
В =
,
В =
![]() .
.
Решение.
![]() ;
;
![]()
Пример. Найти произведение матриц А и В.
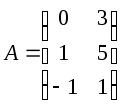 ,
,
![]() .
.
Решение:
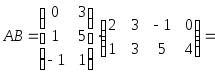
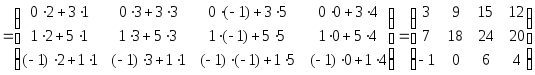
Если АВ=ВА, то матрицы А и В называются коммутативными. Так, например, единичная матрица Е коммутативна с любой квадратной матрицей того же порядка, причем АЕ=ЕА=А.
Скалярная матрица может быть представлена в виде произведения элемента матрицы, стоящего на ее главной диагонали, на единичную матрицу того же порядка:
А=![]() Е.
Е.
Легко видеть, что произведение любой квадратной матрицы на скалярную матрицу того же порядка коммутативно.
Квадратную
матрицу А можно возвести в степень n
, для чего ее надо умножить на саму себя
n
раз, т.е.
![]() .
.
Транспонирование матрицы – это такое преобразование, при котором строки заменяются соответствующими столбцами:
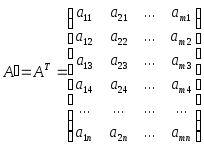
Транспонированная матрица обладает следующими свойствами, которые следуют из определения:
-
(А
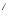 )
)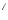 =А;
=А; -
(А+В)
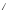 =А
=А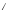 +B
+B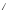 ;
; -
(AB)
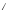 =B
=B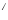 A
A .
.
Если
матрица А – симметрическая, то А![]() =А,
т.е. симметрическая матрица совпадает
со своей транспонированной.
=А,
т.е. симметрическая матрица совпадает
со своей транспонированной.
Очевидно,
что произведение С=АА![]() представляет собой симметрическую
матрицу. Действительно,
представляет собой симметрическую
матрицу. Действительно,
С![]() =(АА
=(АА![]() )
)![]() =(А
=(А![]() )
)![]() А
А![]() =АА
=АА![]() =С.
=С.
При этом А может быть и прямоугольной матрицей произвольного порядка, С же будет квадратной, порядка, соответствующего числу строк матрицы А.
В различных приложениях используется понятие нормы матрицы.
Под
нормой матрицы А=![]() понимается действительное число ||A||,
удовлетворяющее условиям:
понимается действительное число ||A||,
удовлетворяющее условиям:
а)
||A||![]() 0,
причем ||A|| = 0 тогда и только тогда, когда
А=О;
0,
причем ||A|| = 0 тогда и только тогда, когда
А=О;
б)
||![]() A||=|
A||=|![]() |
|![]() ||A||,
(
||A||,
(![]() - число) и, в частности ||-A||=||A||;
- число) и, в частности ||-A||=||A||;
в)
||A+B||![]() ||A||+||B||;
||A||+||B||;
г)
||AB||![]() ||A||
||A||![]() ||B||,
||B||,
где А и В – матрицы, для которых соответствующие операции имеют смысл.
Для
матрицы А=(а![]() )
)![]() произвольного типа рассматриваются
главным образом три вида норм:
произвольного типа рассматриваются
главным образом три вида норм:
|
1)
||A|| |
(m – норма); |
|
2)
||A|| |
(l – норма); |
|
3)
||A|| |
(k – норма). |
Все они удовлетворяют перечисленным выше условиям.
