
- •Оглавление
- •1. Задача № 7 3
- •Задача № 7
- •2. Задача № 10
- •3. Задача № 17
- •4. Вопрос № 46. Цифровые измерители сопротивления, емкости и добротности, в которых используются свойства затухающих процессов.
- •5. Вопрос № 36. Измерительные трансформаторы напряжения. Схема включения , основные уравнения, векторная диаграмма, погрешности.
- •6. Вопрос № 66. Мостовые схемы переменного тока для измерения емкости и угла потерь. Вывод условий равновесия. Особенности.
- •Литература
4. Вопрос № 46. Цифровые измерители сопротивления, емкости и добротности, в которых используются свойства затухающих процессов.
Ответ
4.1 Цифровые измерители сопротивления и ёмкости.
Цифровое
измерение параметров R,
C
осуществляется, либо прямым преобразование
их в напряжение, частоту или интервал
времени, например, с использованием
свойств затухающего процесса, либо
уравновешиванием с использованием
цифровых мостов постоянного и переменного
тока. Цифровые измерители R,
, C
с преобразованием
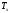 и
и
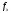 имеют менее сложную схему. Цифровые
измерители R,
C
на основе мостов переменного тока более
сложные по устройству, однако обладают
более высокой точностью. Их недостатком
является измерение R,
C
только на нескольких фиксированных
частотах. Разработаны широкодиапазонные
цифровые приборы переменного тока, при
помощи которых можно определять частотные
характеристики параметров R,
C
в широком частотном диапазоне.
имеют менее сложную схему. Цифровые
измерители R,
C
на основе мостов переменного тока более
сложные по устройству, однако обладают
более высокой точностью. Их недостатком
является измерение R,
C
только на нескольких фиксированных
частотах. Разработаны широкодиапазонные
цифровые приборы переменного тока, при
помощи которых можно определять частотные
характеристики параметров R,
C
в широком частотном диапазоне.
В
апериодическом затухающим процессе
интервал времени между началом процесса
затухания, когда напряжение равно
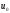 , и моментом, когда напряжение уменьшается
до
, и моментом, когда напряжение уменьшается
до
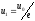 ,
равен постоянной времени цепи
,
равен постоянной времени цепи
 . Постоянная времени активно-емкостной
цепи равна RC.
Следовательно, при известном постоянном
значении R
и С постоянная времени пропорциональна
С или R.
. Постоянная времени активно-емкостной
цепи равна RC.
Следовательно, при известном постоянном
значении R
и С постоянная времени пропорциональна
С или R.
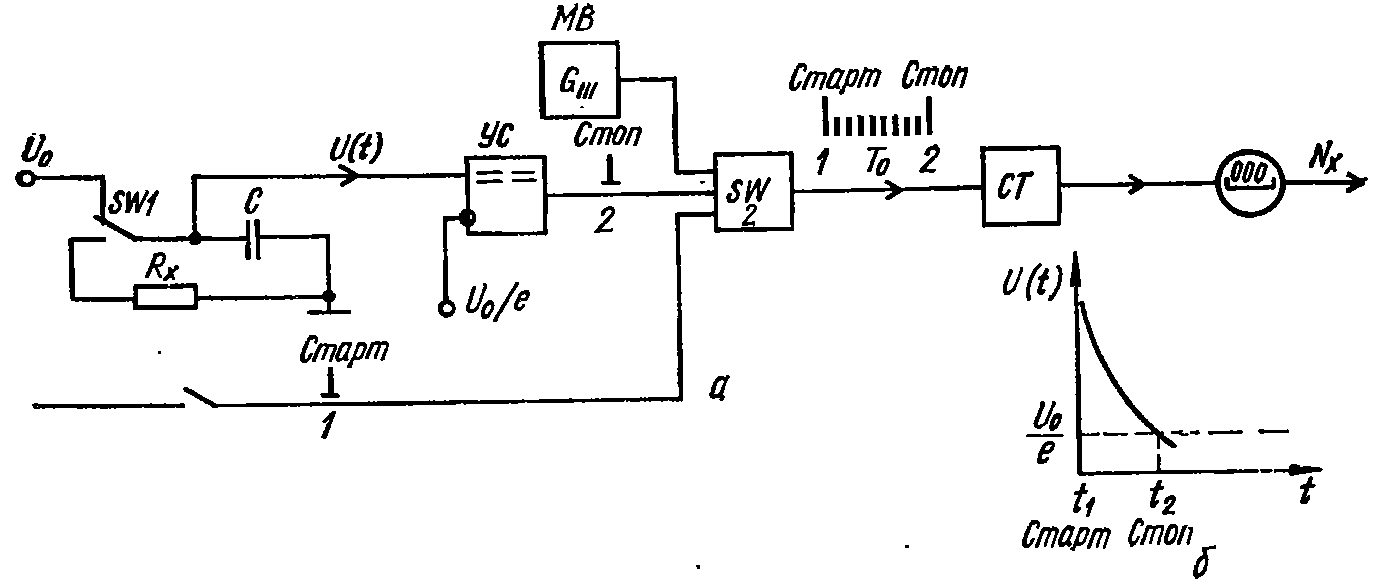
Рисунок 4.1 - Структура цифрового измерителя сопротивления и ёмкости.
Например,
в таком цифровом омметре измеряемое
сопротивление
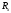 включается(рис 4.1 а,б) параллельно
конденсатору с постоянной и известной
емкостью С. В момент начала измерения
включается(рис 4.1 а,б) параллельно
конденсатору с постоянной и известной
емкостью С. В момент начала измерения
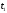 конденсатор С, заряженный до напряжения
конденсатор С, заряженный до напряжения
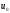 ,
подключается к сопротивлению
,
подключается к сопротивлению
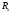 ,
открывается ключ SW
и через него начинают поступать на
счётчик квантующие импульсы
,
открывается ключ SW
и через него начинают поступать на
счётчик квантующие импульсы
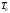 .
Напряжение на конденсаторе снижается,
и в момент
.
Напряжение на конденсаторе снижается,
и в момент
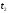 ,
когда это напряжение становится равным
,
когда это напряжение становится равным
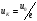 , срабатывает УС и закрывает ключ SW.
, срабатывает УС и закрывает ключ SW.
Интервал
времени между моментами
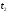 и
и
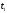 равен постоянной времени цепи
равен постоянной времени цепи
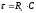 . Тогда отсчёт счетчика импульсов
. Тогда отсчёт счетчика импульсов
![]()
Если
С известно и постоянно, то показания
счётчика можно представить в Омах. При
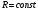 прибор можно использовать для цифрового
измерения С.
прибор можно использовать для цифрового
измерения С.
4.2 Цифровые измерители добротности
Принцип действия цифрового измерителя добротности основан на постоянстве логарифмического декремента затухания амплитуд и периода колебаний- важных свойств затухающих колебаний.
Логарифмический декремент затухания
![]() (4.1)
(4.1)
где
N-
число периодов колебаний между амплитудами
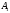 и
и
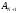 ;
;
 -
амплитуда первого колебаний;
-
амплитуда первого колебаний;
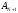 -амплитуда
(N+1)-го
колебаний;
-амплитуда
(N+1)-го
колебаний;
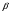 -
степень затухания колебаний.
-
степень затухания колебаний.
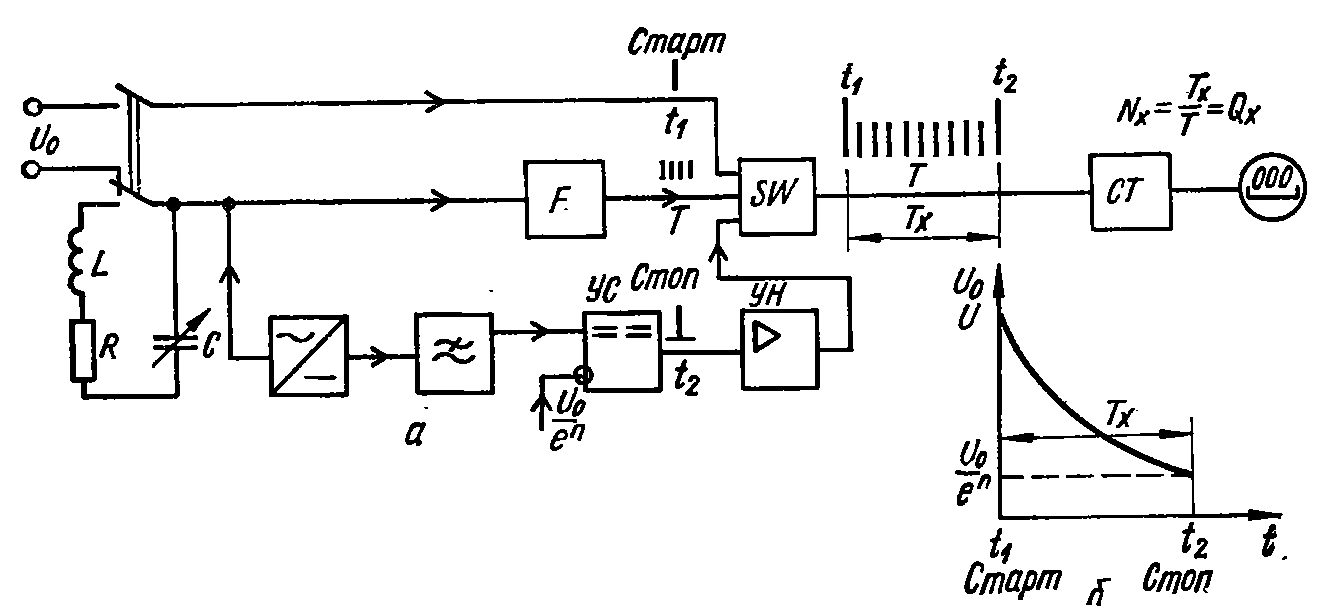
Рисунок 4.2 - Структура цифрового измерителя добротности.
Измеряемой
величиной является добротность катушки
индуктивности
![]() .
Эта катушка включается в колебательных
контур на входе прибора(рис 4.2 а,б) .
.
Эта катушка включается в колебательных
контур на входе прибора(рис 4.2 а,б) .
Перед
запуском цифрового измерителя добротности
конденсатор входного колебательного
контура С заряжен до потенциала, равного
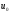 .
В момент запуска
.
В момент запуска
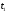 открывается ключ SW,
входной колебательный контур замыкается
и на формирователь F
подаются затухающие колебания с частотой
открывается ключ SW,
входной колебательный контур замыкается
и на формирователь F
подаются затухающие колебания с частотой
 ,
которые возникают во входном колебательном
контуре. С выхода формирователя на
счётчик через ключ SW
проходят импульсы с периодом повторения
,
которые возникают во входном колебательном
контуре. С выхода формирователя на
счётчик через ключ SW
проходят импульсы с периодом повторения
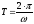 . Эти же затухающие колебания подаются
на выпрямитель и фильтр на выделения
огибающей, которая подается на первых
вход УС. На второй вход УС подано
постоянное напряжение
. Эти же затухающие колебания подаются
на выпрямитель и фильтр на выделения
огибающей, которая подается на первых
вход УС. На второй вход УС подано
постоянное напряжение
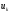 .
В момент
.
В момент
 ,
когда напряжение огибающей колебаний
после фильтра станет равным и, срабатывает
УН и выдает стоп-импульс, который
закрывает ключ SW.
Покажем, что число импульсов
,
когда напряжение огибающей колебаний
после фильтра станет равным и, срабатывает
УН и выдает стоп-импульс, который
закрывает ключ SW.
Покажем, что число импульсов
 с периодом повторения
с периодом повторения
 ,
подсчитанных за это время счётчиком,
при определённых условиях равно числовому
значению добротности катушки индуктивности
,
подсчитанных за это время счётчиком,
при определённых условиях равно числовому
значению добротности катушки индуктивности
![]() . Из уравнения для логарифмического
декремента затухания (4.1) получаем:
. Из уравнения для логарифмического
декремента затухания (4.1) получаем:
![]() (4.2)
(4.2)
Где
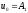 –амплитуда
первого колебания;
–амплитуда
первого колебания;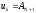 -амплитуда (N+1)-го
колебания.
-амплитуда (N+1)-го
колебания.
Для электрического колебательного контура степень затухания
![]() (4.3)
(4.3)
где
![]() -
период свободных, не затухающих колебаний
контура при отсутствии потерь.
-
период свободных, не затухающих колебаний
контура при отсутствии потерь.
После подстановки (4.3) в (4.2) получим:
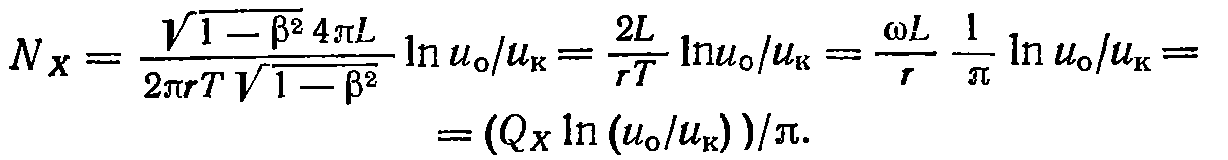
Если
выполнено условие
 ,
то
,
то
![]() .
.
Прибор,
представленный на рис 4.2 , про постоянстве
добротности контура может быть использован
для измерения напряжения
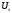 или малых токов
или малых токов
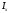 .
.
Цифровой отсчет счётчика
![]()
где t- время зарядки емкости С током .
Нестабильность Q создаёт погрешность в показаниях.
Время открытого состояния ключа
![]()
Тогда
после цифрового измерения
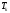 получим:
получим:
![]()
На этом принципе основан, цифровой измеритель типа LCR фирмы «Good Will Instrument Co., Ltd», который имеет вид показанный на рисунке 4.3 и основные характеристики приведенные в таблице 4.1.

Рисунок 4.3 - Передняя панель цифрового измерителя типа LCR
Таблица 4.1-Основные характеристики измерителя типа LCR
|
Характерис тики |
Параметры |
Значения |
|
Измеряемые параметры |
Сопротивление (R,Z,X) |
До 100 МОм с разрешением 0,1 мОм |
|
Сопротивление на постоянном токе (Rdc) |
До 100 МОм с разрешением 0,01 мОм |
|
|
Проводимость (G,Y,B) |
До 1000 См с разрешением 10 нСм |
|
|
Ёмкость (C) |
До 1 Ф с разрешением до 0,01 пФ |
|
|
Индуктивность (L) |
До 100 кГн с разрешением до 0,1 нГн |
|
|
Добротность (Q) |
0,1 – 10000 |
|
|
Тангенс угла потерь (D) |
0,00001 – 1000 |
|
|
Фазовый
сдвиг ( |
-180…180 |
|
|
Базовая погрешность |
|

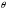 )
)
 0,1
% (R, Z, X, G, Y, B, L, C)
0,1
% (R, Z, X, G, Y, B, L, C)