6. Наибольшее и наименьшее значения функции на отрезке
Теорема. Непрерывная на отрезке функция достигает на этом отрезке своих наибольшего и наименьшего значений. Наибольшее и наименьшее значения функция имеет либо в точках экстремума, либо на концах отрезка.
Согласно этому утверждению можно использовать следующий алгоритм исследования на нахождение наибольшего (наименьшего) значения функции на отрезке:
1) проверить непрерывность функции на отрезке;
2) определить точки, подозрительные на экстремум;
3) вычислить значения функции в точках п. 2 и на концах отрезка;
4) выбрать наибольшее и наименьшее значения функции из значений п. 3;
5) записать ответ.
Пример 5.13. Найти наибольшее и
наименьшее значения функции
,
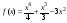заданной на отрезке
.
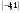Решение.
1. Функция
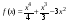непрерывна.
2. Вычислим производную
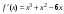и, приравняв ее к нулю, найдем точки,
подозрительные на экстремум:
.
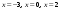Других точек, подозрительных на экстремум
нет. Точка
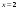не принадлежит заданному отрезку,
следовательно, остаются две точки внутри
области и граничные точки, в которых и
вычислим функцию.
3.
.
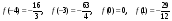4. Выбираем наибольшее и наименьшее
значения:
.
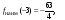
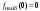Ответ:
.
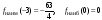Пример 10. Найти наибольшее и наименьшее
значения функции
,
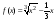заданной на отрезке
.
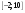Решение.
1. Функция
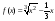непрерывна.
2. Вычислим производную
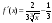и, приравняв ее к нулю, найдем точку,
подозрительную на экстремум:
.
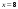Кроме этой точки есть еще точка
,
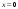в которой возможен экстремум, так как
в этой точке не существует конечная
производная.
3. Вычислим значения функции в найденных точках и на концах отрезка:
.
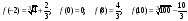4. Выбираем наибольшее и наименьшее значения.
Ответ:
.
Индивидуальное задание
Каждый студент должен построить два графика:
1.
,
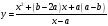2.
.
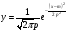Параметры:
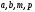- для каждого студента заданы в таблице
согласно номеру в журнале .
|
№ |
a |
b |
m |
p |
№ |
a |
b |
m |
p |
|
1 |
1 |
3 |
1 |
1 |
16 |
-3 |
1 |
1 |
1 |
|
2 |
2 |
3 |
2 |
2 |
17 |
3 |
2 |
2 |
1 |
|
3 |
-1 |
2 |
3 |
3 |
18 |
2 |
4 |
3 |
1 |
|
4 |
-2 |
1 |
-1 |
1 |
19 |
1 |
-2 |
-1 |
2 |
|
5 |
3 |
1 |
-2 |
2 |
20 |
1 |
3 |
-2 |
2 |
|
6 |
-2 |
2 |
-3 |
3 |
21 |
2 |
-3 |
-3 |
2 |
|
7 |
3 |
-1 |
1 |
2 |
22 |
-1 |
4 |
1 |
3 |
|
8 |
3 |
2 |
2 |
3 |
23 |
-1 |
-4 |
2 |
3 |
|
9 |
3 |
-2 |
3 |
1 |
24 |
4 |
-1 |
3 |
3 |
|
10 |
2 |
-1 |
-1 |
2 |
25 |
-3 |
-2 |
-1 |
2 |
|
11 |
-1 |
4 |
-2 |
3 |
26 |
1 |
-3 |
-2 |
2 |
|
12 |
2 |
-3 |
-3 |
1 |
27 |
2 |
1 |
-3 |
2 |
|
13 |
4 |
1 |
1 |
3 |
28 |
1 |
2 |
-4 |
1 |
|
14 |
4 |
2 |
2 |
2 |
29 |
2 |
3 |
4 |
1 |
|
15 |
4 |
3 |
3 |
1 |
30 |
3 |
2 |
4 |
1 |