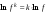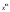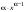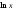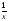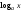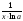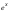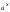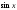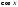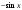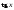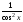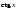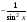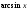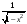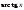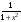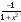4. Производная функции
Пусть функция
 определена
в точке
определена
в точке
 и ее окрестности. Если существует
конечный предел
и ее окрестности. Если существует
конечный предел
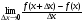 , (3)
, (3)
то этот предел называется производной
функции в точке
 и обозначается
и обозначается
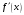 или
или
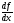 .
.
При существовании односторонних пределов
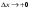 или
или
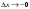 говорят о существовании односторонних
производных.
говорят о существовании односторонних
производных.
Функция, имеющая в каждой точке промежутка конечную производную, называется дифференцируемой функцией на этом промежутке.
Вычисляется производная с использованием таблицы производных и согласно правилам дифференцировании.
|
|
|
Правила дифференцирования |
|
const |
0 |
АЛГОРИТМ вычисления производных:
Замечание.
Выражения
следует
предварительно преобразовать по
формулам:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Производная от первой производной
называется второй
производной или производной второго
порядка и обозначается
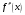 или
или
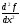 .
Аналогично определяются производные
более высоких порядков.
.
Аналогично определяются производные
более высоких порядков.
Геометрический смысл производной.
Пусть функция непрерывна на промежутке
в окрестности точки
 ,
а график функции имеет в этой точке
касательную, не параллельную оси
,
а график функции имеет в этой точке
касательную, не параллельную оси
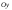 .
Тогда
.
Тогда
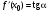 ,
(4)
,
(4)
где
 –
угол между положительным направлением
оси
–
угол между положительным направлением
оси
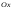 и
касательной (рис. 1).
и
касательной (рис. 1).

Рис. 1
Уравнение касательной к графику функции
в точке
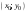 имеет вид
имеет вид
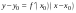 .
(5)
.
(5)
Пример 3. Найти производную функции
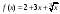 в точке
в точке
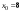 .
.
Решение.
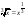 .
.
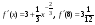 .
.
Пример 4. Найти производную функции
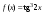 в точке
в точке
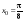 .
.
Решение. Заданная функция – сложная. Используем формулу дифференцирования сложной функции.
Тогда
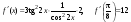 .
.
Правило Лопиталя
Теорема.
Пусть функции 1)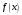 и
и
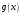 определены
в окрестности точки
определены
в окрестности точки
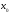 и существуют конечные производные, 2)
и существуют конечные производные, 2)
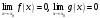 ,
3) существуют конечные производные
,
3) существуют конечные производные
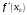 и
и
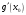 ,
причем
,
причем
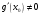 ,
4) существует предел
,
4) существует предел
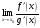 ,
Тогда
,
Тогда
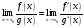 .
●
.
●
Здесь
приведена одна из теорем Лопиталя.
Аналогичное правило вычисления предела
справедливо д с неопределенностью
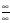 .
.
Примеры вычисления пределов с помощью правила Лопиталя:
1.
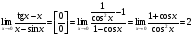 ,
,
2. ,
,
3.
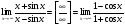 .
.
Во втором примере мы применили правило Лопиталя 4 раза. В третьем примере правило Лопиталя не применимо, так как не существует предела производных. Нет лекарства от всех бед. Предел же легко вычисляется с использованием теорем и равен единице.
Рекомендуем запомнить пределы:
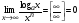 ,
,
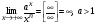 .
.

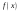
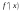
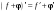 .
.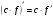 .
.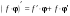 .
.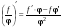 .
.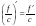 .
.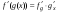 (дифференцирование
сложной функции)/
(дифференцирование
сложной функции)/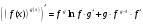 .
.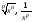 ,
,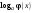
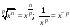 ;
; ;
;
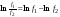 ;
;