10

Электропроводность электролитов

Сопротивление R (Ом) любого проводника, в том числе и электролита, зависит от его природы, сечения S (см²), по которому течет ток, и длины (см).

(1)

где – коэффициент пропорциональности, называемый удельным сопротивлением (очевидно, если = 1 см и S = 1 см², то R = ).

Удельное сопротивление – сопротивление проводника сечением 1 см² и длиной 1 см, т.е. это сопротивление 1 см³ или для раствора – 1 мл. имеет размерность (Ом * см).

Электропроводность – величина, обратная сопротивлению. Удельная электропроводность  (каппа) равна .

= (Ом^-1 * см^-1) (2)

Электрический ток в растворе переносится ионами. Чем больше ионов в растворе, чем большее их число содержится в 1 см³, тем больше удельная электропроводность .

Для определения нужно согласно выражению (1) найти сопротивление R и, зная и S проводника, вычислить 1/= . Но изготовление сосуда с электродами, для которого и S были бы точно известны, технически трудно. Поэтому применяют сосуды, удобные в изготовлении и работе, но с неизвестными и S.

Н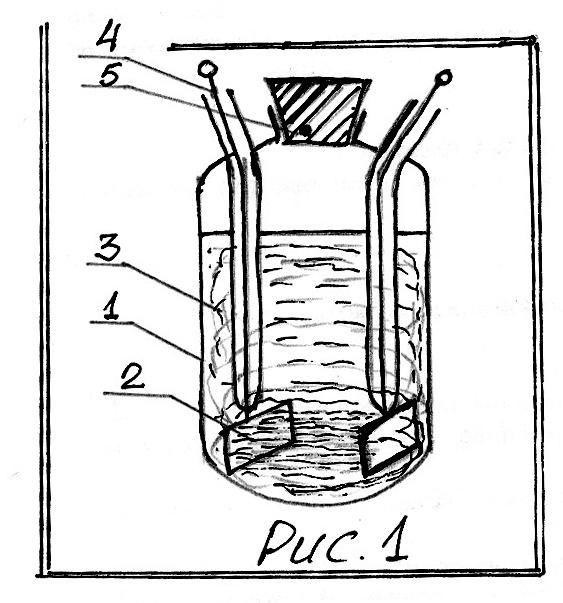а рис.1 представлена схема сосуда, применяемого для определения (сосуд Аррениуса), где

1. стеклянный сосуд;

2. Pt-электроды;

3. электролит;

4. токоподводы в стеклянных трубках;

5. пробка.

На рис.1 представлена также схема распределения тока между двумя Pt-электродами, помещенными в сосуд с электролитом. Ток проходит не по кратчайшему пути от электрода к электроду. Поэтому невозможно найти величину /S, определяющую сопротивление.

Поэтому при определении электропроводности в таких сосудах отношение /S рассматривают как постоянную величину, характерную для сосуда данных размеров и формы при данном расположении электродов и постоянном объеме раствора (в нашем случае – 20 мл).

Тогда R = или (3)

Величина K называется постоянной сосуда, или емкостью сопротивления сосуда, т.к. показывает сколько удельных сопротивлений содержится в сосуде с сопротивлением R (см.(3)).

Формула (3), с учетом, что = 1/ , принимает вид:

K = R (4).

Для определения опытным путем K используют электролит, для которого известно. Обычно это 0,1 М раствор KCl, для которого при 25°C равна 0, 01288 Ом^-1см^-1.

Измерение сопротивления R проводятся при помощи моста сопротивления, питаемого переменным током (рис.2).

R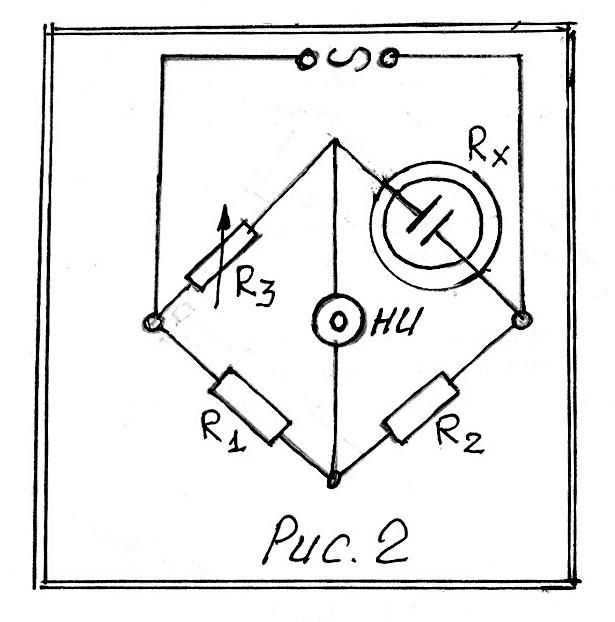_x – измеряемое сопротивление;

R₁, R₂, и R₃ – изменяемые сопротивления;

НИ – индикатор.

Условие баланса моста может быть представлено пропорцией (5):

(5)

Отсюда искомая величина R_х вычисляется как

R_х= R₃ (6)

В случае, если R₂ = R₁, R_x = R₃.

Электропроводность электролита зависит от его концентрации, а последняя не фигурирует в формуле для расчета , т.к. удельная электропроводность – это электропроводность 1 см³ раствора. Поэтому для понимания свойств электролитов представляет величину мало удобную.(Но зато ее можно получить непосредственным измерением).

Пересчитав , можно найти величину, связанную с концентрацией электролита – эквивалентную электропроводность λ (лямбда), которую ввел в науку Э.Х.Ленц.

На рис.3 представлена схема, поясняющая связь между удельной () и эквивалентной (λ) электропроводностью.

Допустим, что имеем произвольный объем раствора, в котором содержится 1 г-экв электролита. Поместим мысленно этот раствор в плоский сосуд шириной 1 см. Противоположные стенки его (А и В на рис.3) сделаны из листовой платины. Прочие размеры таковы, что залитый в этот сосуд раствор содержит 1 г-экв растворенного вещества.

Объем раствора в плоском сосуде, например, n см³. Каждый из n кубиков в сосуде (см. рис.3) имеет электропроводность (удельную). Ток проходит между поверхностью А и В. Следовательно, все кубики включены параллельно.

Суммарная электропроводность n кубиков:

λ = n (7).

Каждый кубик содержит 1/n г-экв, т.е. концентрация раствора С составляет (в г-экв/мл):

(8)

Поэтому уравнение (7) можно переписать, выразив λ в (Ом^-1 * см²), так

λ = (9)

или, переходя от (мл) к (л), заменим С на С₀ (г-экв/л):

λ = (10)

Если бы выбранный объем раствора содержал 1 моль растворенного вещества, то мы бы имели молярную электропроводность μ (мю). Соотношение (10) осталось бы неизменным, только С₀ представляло бы концентрацию в молях на 1 л.

λ при разбавлении раствора может только возрастать, т.к. разбавление увеличивает степень диссоциации (α) вещества на ионы и при данном количестве растворенного вещества (1 г-экв) в объеме раствора растет абсолютное число ионов.

П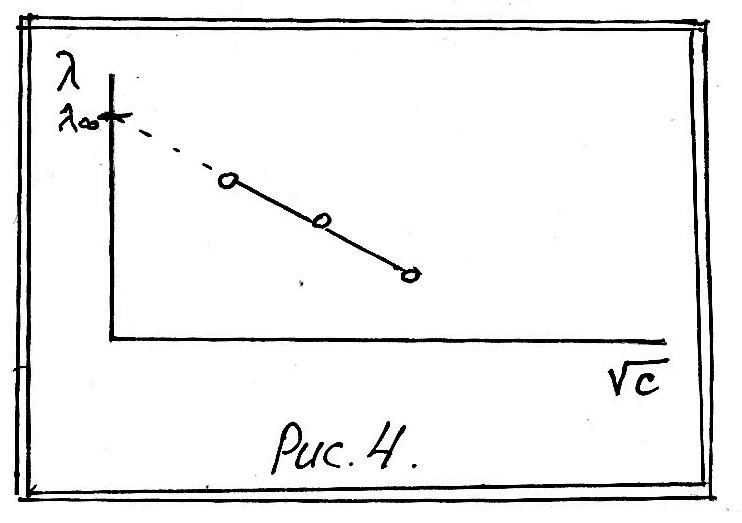редельное значение λ при α=1 называется эквивалентной электропроводностью при бесконечном разбавлении и обозначается λ∞. Для нахождения λ∞ проводят определение для ряда последовательно убывающих концентраций, вычисляют для них значения λ, наносят на график в координатах λ – √C и экстраполяцией определяют λ∞ (рис.4).

Одним из основных, в сущности, недоказанных положений теории электролитической диссоциации было утверждение, что степень диссоциации α равна отношению электропроводности λ при данном разбавлении (для которого определяется λ) к λ∞

α = (11)

В этом случае α представляет собой коэффициент электропроводности.

Примечание: Степенью диссоциации α называется отношение числа молекул, распавшихся на ионы, к общему числу молекул, введенных в раствор. Так, если в раствор было введено n₂ молекул (или молей), а на ионы из них распалось (продиссоциировало) n' молекул (или молей), то степень диссоциации

α = (12)

Очевидно, что степень диссоциации α может меняться от нуля (диссоциации нет) до 1 (полная диссоциация)

0 ≤ α ≤ 1

Степень диссоциации α зависит от природы растворенного вещества и растворителя, а также от концентрации раствора.

По теме «Электропроводность растворов электролитов» выполняется две лабораторные работы. Работа № 1 посвящена определению удельной и эквивалентной электропроводности растворов. Работа № 2 дает возможность с помощью метода кондуктометрического титрования определить концентрацию раствора электролита.

Работа № 1

Определение электропроводности раствора электролита

Для работы необходимо иметь:

– сосуд Аррениуса;

– мерная колба (100 мл);

– 2 пипетки на 10 и 20 мл;

– стеклянный стаканчик;

– воронка;

– термостат на 25°C;

– аналитические весы;

– мост переменного тока;

– дистиллированная вода.

Порядок проведения работы

1. Получить сосуд Аррениуса у лаборанта, вылить из него дистиллированную воду, залить в него 20 мл 0,1 н раствора KCl, поместить сосуд в термостат на 25°C.

2. Получить у лаборанта соль для приготовления раствора электролита заданной концентрации.

Рассчитать навеску для приготовления раствора.

Пример расчета навески.

Допустим, требуется приготовить 100 мл раствора, содержащего 1/32 г-экв/л соли. Если эквивалент соли равен M/z (г), где M – молекулярная масса соли, а z – суммарная валентность катиона или аниона (для NaCl z = 1; для CuSO₄ z = 2 и т.п.), то в 100 мл содержится г или для концентрации 1/32 г-экв/л.

Так, для NaCl M = 23 + 35,5 = 58,5 г. z = 1. Величина навески:

X= =0,1828 г.

Для CuCl₂ М = 64 + 71 = 135 г; z = 2

Х==0,211 г.

Взвешивание навески производится на аналитических весах с точностью как минимум до 3-го знака после запятой.

3. Перенести навеску с помощью воронки в мерную колбу на 100 мл, залить в колбу примерно 30 мл дистиллированной воды, в которой полностью растворить навеску соли, после чего долить воды до 100 мл.

4. Измерить с помощью моста переменного тока, подключив к нему сосуд Аррениуса, сопротивление раствора 0,1 н KCl. Измерения проводить несколько раз так, чтобы последние два измеренных сопротивления были одинаковыми. Если R = const, значит, сосуд нагрелся до 25°C.

5. Определив сопротивление 0,1 н KCl, рассчитать постоянную сосуда К.:

K= *R_изм=0,01288*R_изм

Полученное значение К показать преподавателю.

6. Вылить из сосуда Аррениуса, отсоединив от него провода, раствор KCl, сполоснуть сосуд дистиллированной водой и раствором задачи. Залить с помощью стаканчика и пипетки на 20 мл в сосуд 20 мл исследуемого раствора и поместить сосуд в термостат на 25°C.

7. Через 5 минут провести первое измерение R раствора и далее измерять через 3 – 5 мин. Повторять измерения до достижения постоянства R.

8. Рассчитать и λ для заданного раствора:

=; λ=.

Показать результат преподавателю.

9. Приготовить вторую концентрацию раствора. Если первая С₁ = 1/32 моля, а вторая С₂ = 1/64 моля, то надо из сосуда Аррениуса с помощью пипетки на 10 мл оттянуть 10 мл раствора первой концентрации и, промыв пипетку на 10 мл дистиллированной водой, добавить в сосуд Аррениуса 10 мл воды.

10. Сосуд снова помещают в термостат на 25°C и проводят измерения R для второй концентрации так же, как в п.7.

11. Рассчитать и λ для концентрации 1/64 моля и показать результат преподавателю. Работа окончена.

12. Вылить из сосуда Аррениуса раствор, залить в него дистиллированную воду, вымыть использованную посуду и сдать лаборанту рабочее место.

В отчете должно быть:

– теоретическая часть;

– схемы прибора и сосуда;

– расчеты К, , λ и α = λ/ λ∞, а также график λ–√C для определения λ∞.