
- •Содержание
- •Раздел 1. Дифференциальное исчисление
- •Тема 1. Предел и непрерывность функции
- •Тема 2. Дифференциальное исчисление функций одной переменной
- •Тема 3. Дифференциальное исчисление функций нескольких переменных
- •Раздел 2. Интегральное исчисление. Дифференциальные уравнения. Ряды
- •Тема 4. Интегралы
- •Тема 5. Дифференциальные уравнения
- •5.1. Понятие о дифференциальных уравнениях.
- •5. Линейные дифференциальные уравнения 1-го порядка
- •Тема 6. Ряды
- •6.1. Понятие числового ряда. Необходимое условие сходимости ряда.
- •Раздел 3. Линейная алгебра с элементами аналитической геометрии
- •Тема 7. Векторная алгебра
- •Тема 8. Элементы аналитической геометрии
- •Тема 9. Матрицы и определители
- •Тема 10. Системы линейных уравнений (слу)
- •Раздел 4. Теория вероятностей
- •Тема 12. Основные понятия теории вероятностей. Случайные события и их вероятности
- •Тема 13. Случайные величины и их числовые характеристики
- •Тема 14. Основные распределения случайных величин
- •Тема 15. Функция случайной величины
- •Раздел 5. Элементы математической статистики
- •Тема 18. Выборочный метод
- •Тема 19. Интервальные оценки и проверка гипотез
- •Раздел 6. Линейное программирование и теория игр
- •Тема 20. Задача линейного программирования (лп)
- •П.1.2. Графическое решение задачи лп
- •Тема 21. Симплексный метод линейного программирования
- •Тема 22. Двойственность в линейном программировании
- •Тема 23. Целочисленное программирование
- •Тема 24. Транспортная задача
- •Замкнутая модель тз
- •Тема 25. Матричные и кооперативные игры
- •Раздел 7. Теория оптимального управления и оптимизация на графах
- •Тема 26. Задача динамического программирования
- •Тема 27. Теория оптимального управления
- •Тема 28. Основы теории графов
- •Тема 29. Задача об оптимальном потоке
- •Тема 30. Задача сетевого планирования
- •Раздел 8. Марковские процессы
- •Тема 31. Потоки событий
- •1.1. Простейший поток событий
- •Тема 32. Уравнения Колмогорова
- •1.2. Системы массового обслуживания с отказами
- •1.3Системы массового обслуживания с ограниченной очередью.
- •Тема 33. Системы массового обслуживания
- •1.4 Системы массового обслуживания с ожиданием
- •Раздел 9. Исследование функций и экономическое моделирование
- •Тема 38. Моделирование экономического равновесия и динамики
- •Методические рекомендации и задания для самостоятельной работы студентов
- •Литература Основная
- •Дополнительная
- •Учебно-методическая литература
П.1.2. Графическое решение задачи лп
Задача 1.2.1. Простейшая диета состоит из телятины и хлеба. Содержание в 100 г продукта калорий и холестерина дано в таблице 1.2.1.
Таблица 1.2.1, а
-
Элемент питания
Содержание в
100 г продукта
Норма
потребления
телятина
хлеб
min
max
Калории
600
200
2400
3000
Холестерин
0,15
0,10
0
0,9
Цена
3
0,5
Таблица 1.2.1, б
-
Элемент питания
Содержание в
100 г продукта
Норма
потребления
телятина
хлеб
min
max
Калории
300
200
2400
3600
Холестерин
0,1
0,1
0
1,5
Цена
4
3
Для приведенных данных:
1. Составьте математическую модель задачи.
2. Найдите графически оптимальное решение задачи.
Задача 1.2.3. Имеет ли решение задача линейного программирования:
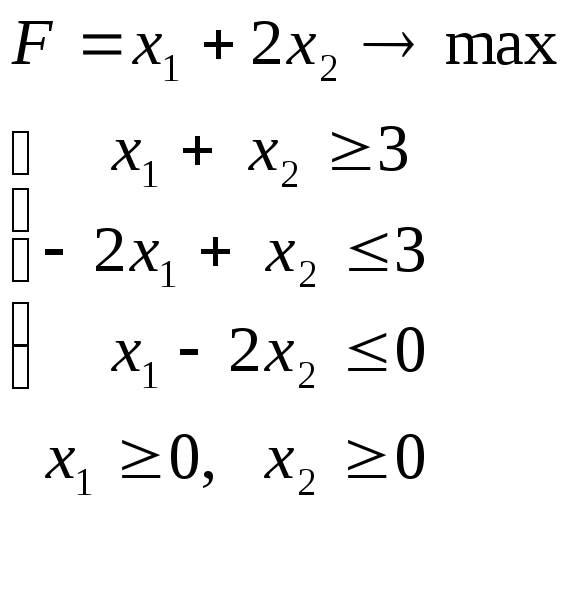
Ответ обоснуйте с помощью графического решения. Как изменится решение, если в условии заменить max на min?
Задача 1.2.4. Решите графически задачу линейного программирования:
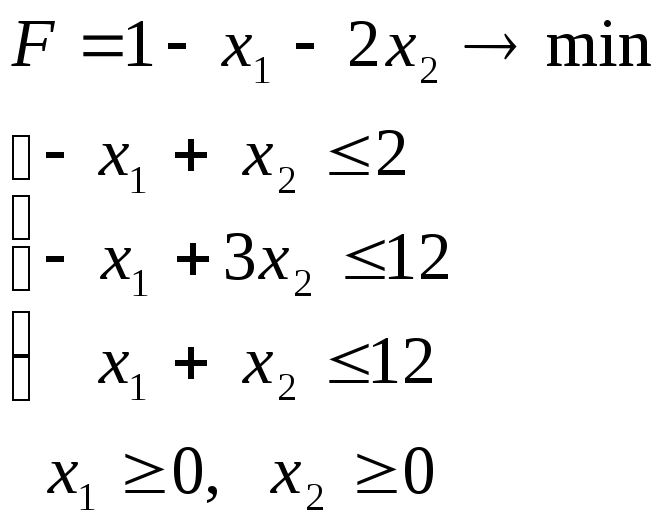
Литература: [2, 4, 5, 7, 15]
Учебно-методическая литература [7, 9]
Тема 21. Симплексный метод линейного программирования
Формула для приращения целевой функции при переходе от одного опорного решения к другому. Формула для расчёта оценок разложений векторов условий по базису опорного решения. Условие для наискорейшего приближения к оптимальному решению. Признак оптимальности опорного решения. Условие существования единственного оптимального решения. Условие существования бесконечного множества оптимальных решений. Признак отсутствия решения ввиду неограниченности целевой функции.
Задача 1.3.1.
а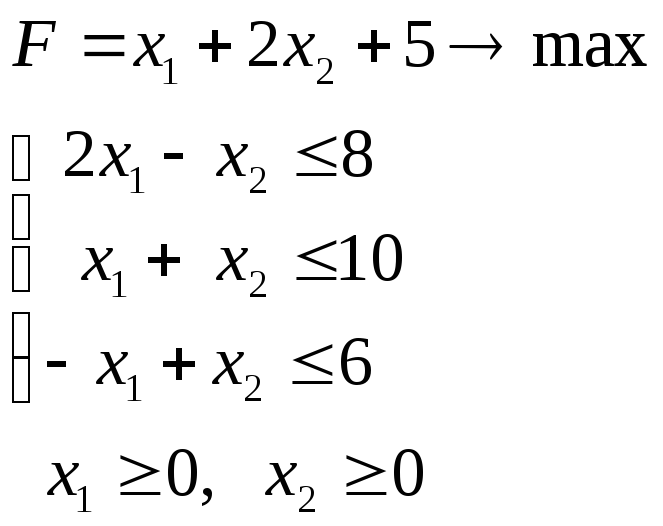 )
)
б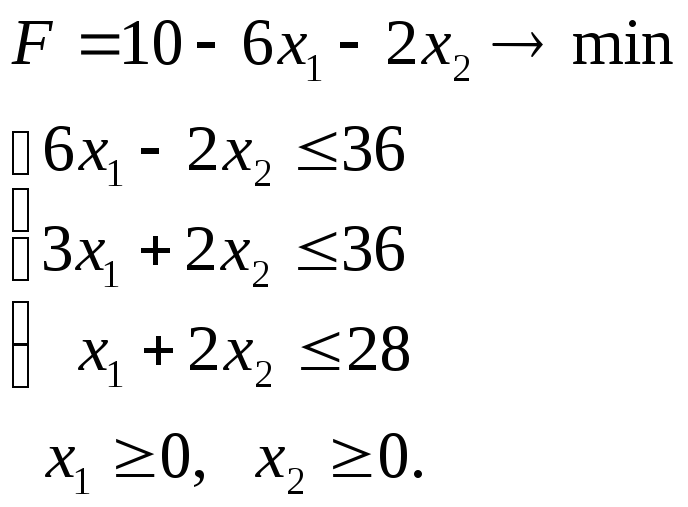 )
)
в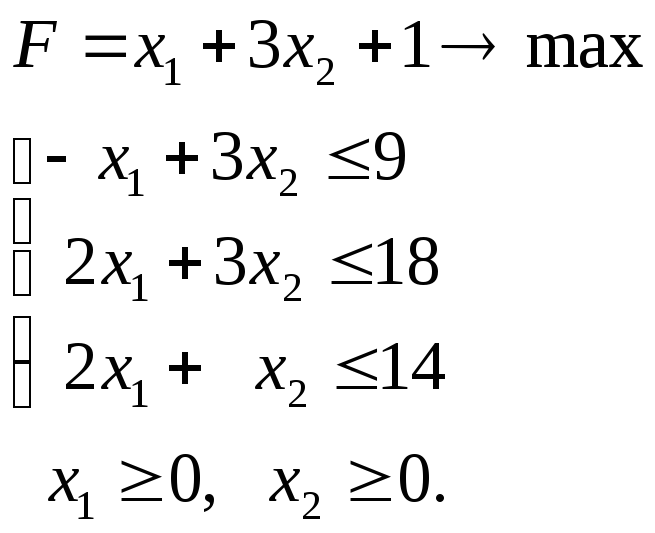 )
)
1. Определите вид задачи ЛП.
2. Приведите задачу к симплексной форме.
3. Решите симплекс-методом.
4. Решите графически.
Задача 1.3.6.
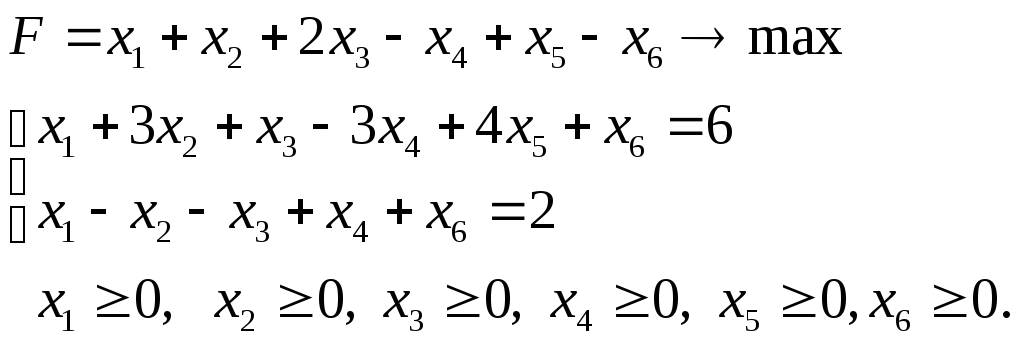
1. Определите вид задачи ЛП.
2. Приведите задачу к симплексной форме.
3. С помощью симплекс-метода определите, имеет ли решение данная задача.
Решите следующие задачи симплекс-методом:
Задача 1.3.7.
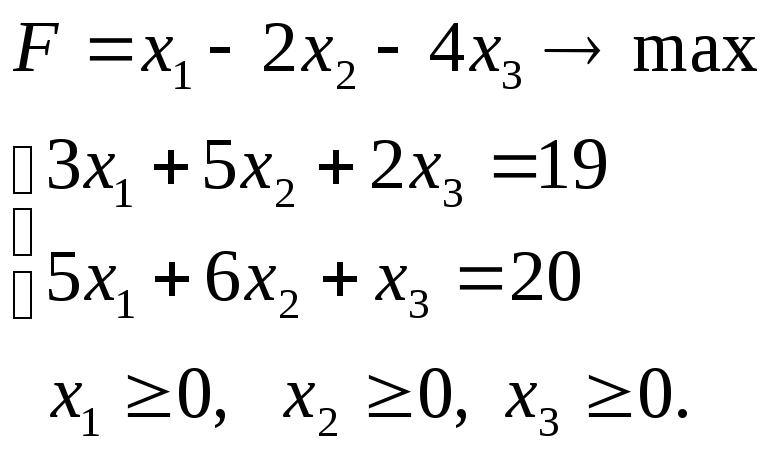
Задача 1.3.8.
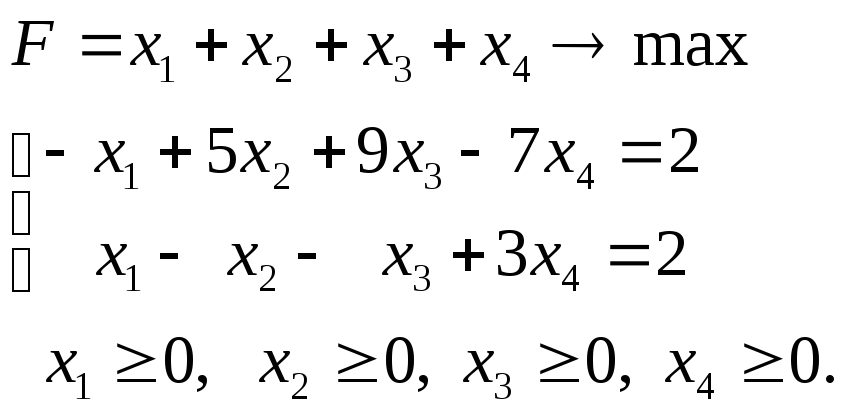
Литература: [2, 4, 5, 7, 15]
Учебно-методическая литература [7, 9]
Тема 22. Двойственность в линейном программировании
Задача.1.4.1. Составьте задачи двойственные к следующим:
а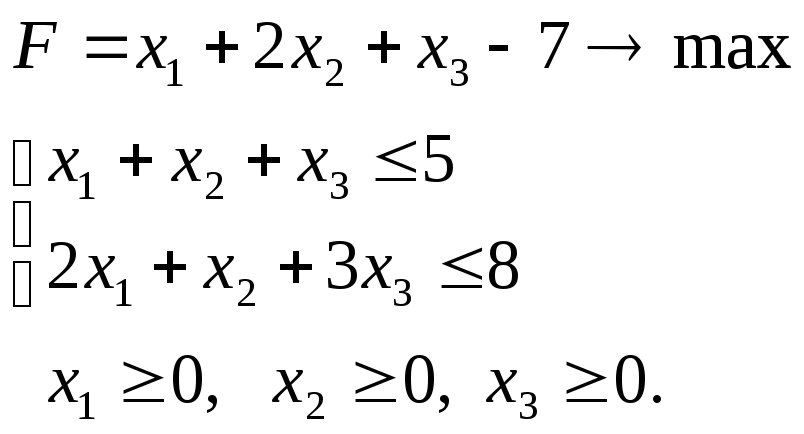 )
)
б )
)
в )
)
Литература: [2, 4, 5, 7, 15]
Учебно-методическая литература [3.4]
