Дополнительная литература:

7. Зимина О.В., Кириллов А.И., Сальникова Т.А. Высшая математика. -2-е изд., испр.-М.: Физико-математическая литература, 2001.-368с.

8. Сборник задач по математике для вузов. Под ред. Котляра Л.М., Углова А.Н. -Наб. Челны: Изд-во КамПИ, 2004.

5. Материалы для контроля знаний студентов.

Итоговой формой контроля знаний является экзамен в конце семестра обучения. На экзамене студент должен показать знание теоретических основ курса в объёме вопросов, приведённых в разделе 5.2 и умение решать задачи, подобные тем, что имеются в его контрольной работе.

Образец решения контрольных задач типового варианта.

1.1 – 30. Вычислить определитель:

а) непосредственным разложением по строке;

б) непосредственным разложением по столбцу;

Решение. а) вычисляем определитель разложением по элементам первой строки: =.

Тогда ==

б) вычисляем определитель непосредственным разложением по элементам второго столбца: =.

Тогда ==.

Ответ: .

2.1-30. а) Найти матрицу , если:

, .

Решение:

1) Транспонируем матрицу : .

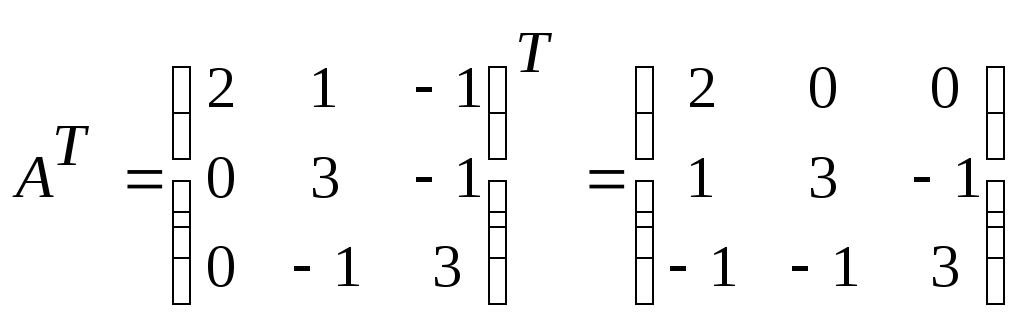2) Вычисляем произведение матриц :

.

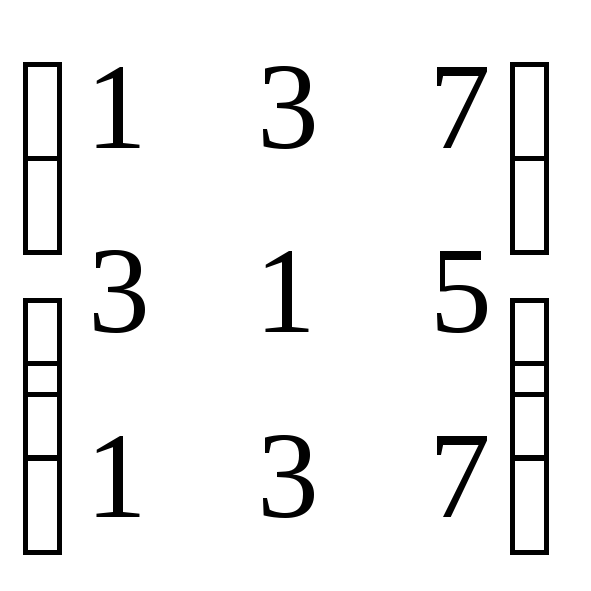3) Находим матрицу :

.

4) Находим матрицу :

.

Ответ: .

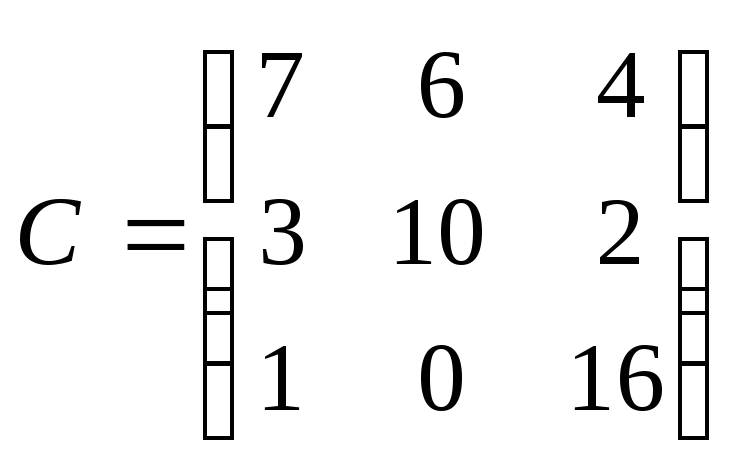3.1 – 30. Дана система уравнений: . Требуется:

а) найти решение системы методом Крамера; б) записать систему в матричном виде и найти её решение методом обратной матрицы; в) найти решение системы методом Гаусса.

Решение.

А) Метод Крамера.

1а) Вычисляем определитель системы и проверяем, что он отличен от нуля:

.

2а) Так как , то система имеет единственное решение, определяемое формулами Крамера:

3а) Вычисляем определители :

,

,

.

4а) Находим решение: .

5а) Выполняем проверку: .

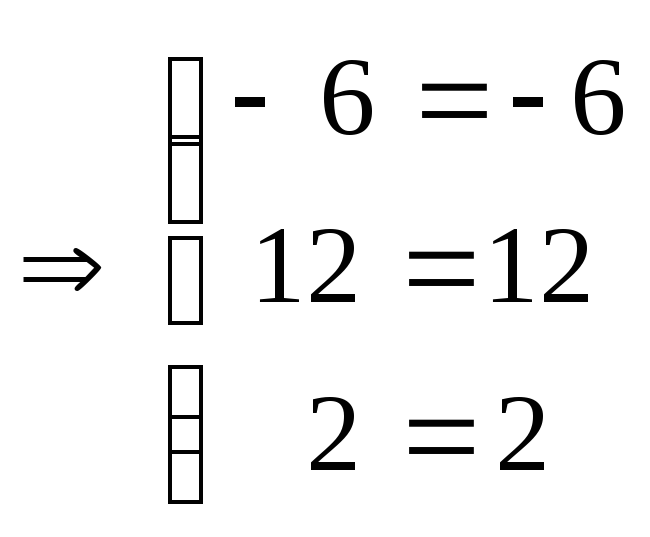Ответ: .

Б) Метод обратной матрицы.

1б) Записываем систему уравнений в матричном виде:

или

2б) Вычисляем определитель системы и проверяем, что он отличен от нуля:

3б) Так как , то матрица системы имеет обратную матрицу и единственное решение системы определяется формулой:

или

4б) Находим обратную матрицу (методом присоединённой матрицы):

.

Тогда .

5б) Находим решение:

.

6б) Выполняем проверку: .

Ответ: .

В) Метод Гаусса.

1в) Записываем расширенную матрицу системы:

.

2в) Выполняем прямой ход метода Гаусса.

В результате прямого хода матрица системы должна быть преобразована с помощью элементарных преобразований строк к матрице треугольного или трапециевидного вида с элементами . Система уравнений, матрица которой является треугольной с элементами , имеет единственное решение, а система уравнений, матрица которой является трапециевидной с элементами , имеет бесконечно много решений.

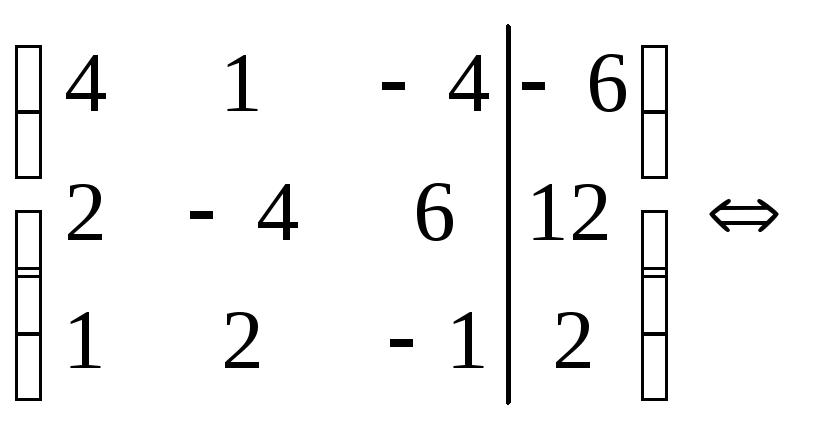
. В результате элементарных преобразований матрица системы преобразована к специальному виду . Система уравнений, матрица которой , является треугольной с ненулевыми диагональными элементами , имеет всегда единственное решение, которое находим, выполняя обратный ход.

Замечание. Если при выполнение преобразования расширенной матрицы в преобразованной матрице появляется строка , где , то это говорит о несовместности исходной системы уравнений.

3в) Выполняем обратный ход метода Гаусса.

Записываем систему уравнений, соответствующую последней расширенной матрице прямого хода: и последовательно из уравнений системы, начиная с последнего, находим значения всех неизвестных:.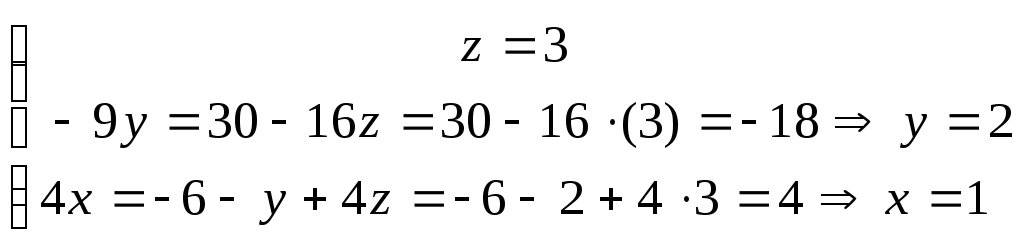

4в) Выполняем проверку: .

Ответ: .

4.1-30. Найти общее решение для каждой из данных систем методом Гаусса:

а) .

Решение.

1а) Записываем расширенную матрицу системы:

.

2а) Выполняем прямой ход метода Гаусса.

.

Матрица системы приведена к трапециевидному виду с ненулевыми диагональными элементами. Соответствующая такой матрице система уравнений имеет бесконечно много решений, которые находим, выполняя обратный ход, и записываем в виде общего решения. Для записи общего решения указываем её базисные и свободные неизвестные. Базисный минор матрицы системы образуют столбцы коэффициентов при неизвестных и : . Поэтому выбираем в качестве базисных – неизвестные и , тогда свободными будут неизвестные и .

3а) Выполняем обратный ход метода Гаусса.

Записываем систему уравнений, соответствующую последней расширенной матрице прямого хода: . Свободным неизвестным придаём разные, произвольные постоянные значения: , , и последовательно из уравнений системы, начиная с последнего, находим значения всех базисных неизвестных: .

Тогда общее решение системы запишется в виде: .

4а) Выполняем проверку:

.

Ответ: .

б) .

Решение.

1а) Записываем расширенную матрицу системы:

.

2а) Выполняем прямой ход метода Гаусса.

Замечание. В результате прямого хода матрица системы должна быть преобразована с помощью элементарных преобразований строк к матрице треугольного или трапециевидного вида с элементами .

Если, при выполнении преобразования расширенной матрицы , в преобразованной матрице появляется строка , где , то это говорит о несовместности исходной системы уравнений.

Для выполнения условия может потребоваться перестановка местами столбцов матрицы системы. Если при выполнении преобразований прямого хода в матрице системы переставлялись местами столбцы коэффициентов при неизвестных, то в дальнейшем, при записи системы уравнений, соответствующей последней расширенной матрице прямого хода, это следует учесть.

.

Матрица системы приведена к трапециевидному виду с ненулевыми диагональными элементами. Соответствующая такой матрице система уравнений имеет бесконечно много решений, которые находим, выполняя обратный ход, и записываем в виде общего решения. Для записи общего решения указываем её базисные и свободные неизвестные. Базисный минор матрицы системы, с учётом перестановки местами столбцов, образуют первый и второй столбцы коэффициентов при неизвестных и : . Поэтому выбираем в качестве базисных – неизвестные и , тогда свободными будут неизвестные и .

3б) Выполняем обратный ход метода Гаусса.

Записываем систему уравнений, соответствующую последней расширенной матрице прямого хода: . Свободным неизвестным придаём разные, произвольные постоянные значения: , , и последовательно из уравнений системы, начиная с последнего, находим значения всех базисных неизвестных: .

Тогда общее решение системы запишется в виде:

4б) Выполняем проверку:

Ответ: .

в) .

Решение.

1в) Записываем расширенную матрицу системы:

.

2в) Выполняем прямой ход метода Гаусса.

.

При выполнении преобразования расширенной матрицы , в преобразованной матрице появилась строка , соответствующая уравнению , которому не удовлетворяет ни один набор значений неизвестных , что говорит о несовместности исходной системы уравнений.

Ответ: Система несовместна.

5.1– 30. Даны векторы : ; ; ; . Требуется: а) вычислить скалярное произведение векторов , если , ; б) вычислить векторное произведение векторов ; в) показать, что векторы образуют базис и найти координаты вектора в этом базисе.

Решение.

1a). Находим вектор

=.

2а) Находим вектор

=.

3а) Вычисляем скалярное произведение векторов :

.

б) Вычисляем векторное произведение векторов :

=

1в) Покажем, что векторы образуют базис . Для этого составим определитель, столбцами которого являются координаты этих векторов и покажем, что он отличен от нуля.

.

Так как , то векторы образуют базис и, следовательно, вектор единственным образом можно разложить по векторам этого базиса.

2в) Записываем разложение вектора по векторам базиса :

или .

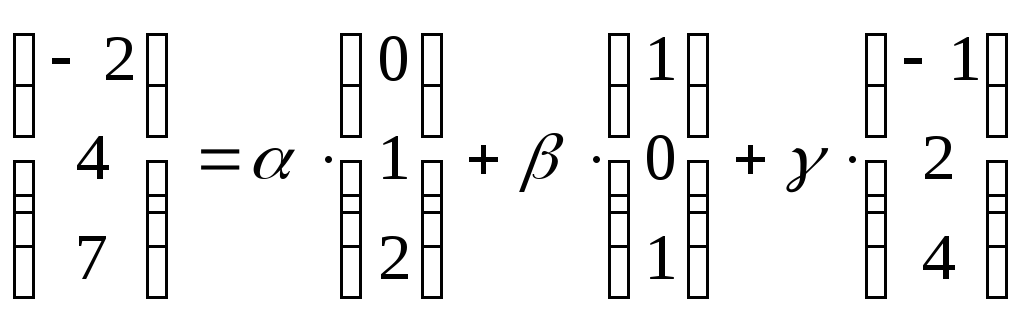Коэффициенты разложения , , называют координатами вектора в базисе и записывают: .

3в) Записываем векторное уравнение относительно ,, в виде эквивалентной ему системы линейных уравнений:, и находим единственное решение системы, например, по формулам Крамера:

, где

,,,.

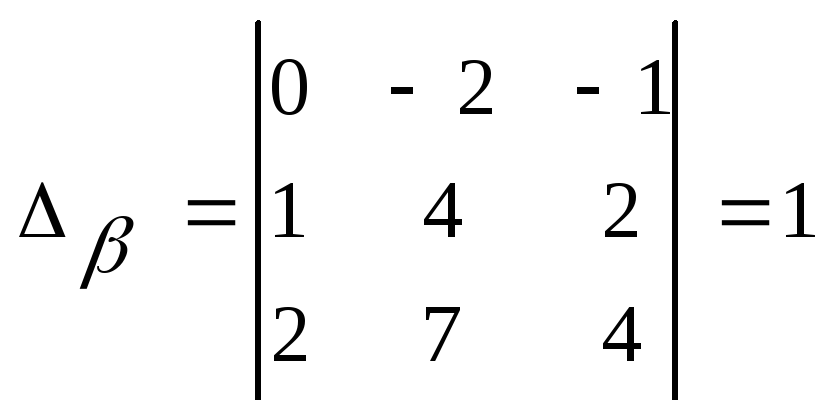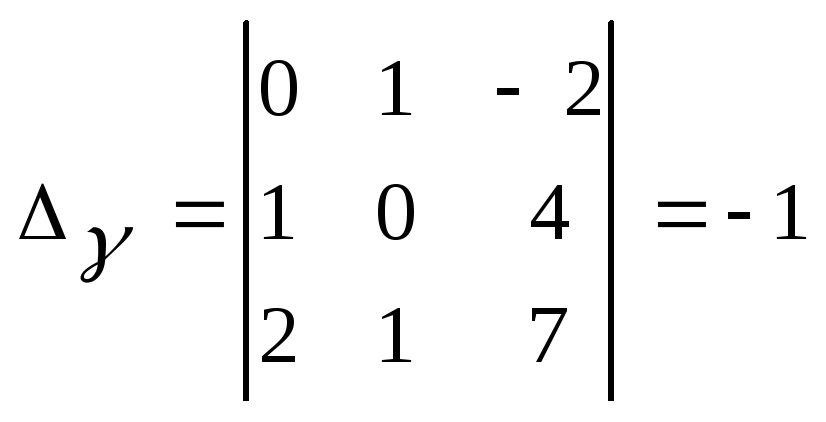Таким образом: , , . Следовательно, разложение имеет вид: или кратко: .

Ответ: .

6.1-30. Даны вершины треугольника : , , Требуется найти:

а) длину стороны ; б) уравнение стороны ;

в) уравнение медианы , проведённой из вершины ;

г) уравнение высоты , проведённой из вершины ;

д) длину высоты ; е) площадь треугольника . Сделать чертёж.

Решение. Сделаем чертёж:

а) Длину стороны находим как длину вектора :

,

.

б) Уравнение стороны находим как уравнение прямой, проходящей через точки и , и записываем его в виде общего уравнения прямой:

.

в) Уравнение медианы находим как уравнение прямой, проходящей через точки и , и записываем его в виде общего уравнения прямой. Неизвестные координаты точки находим как координаты точки, делящей сторону пополам:

; .

Тогда:

.

г) Уравнение высоты находим как уравнение прямой, проходящей через точку перпендикулярно вектору , который принимаем за нормальный вектор прямой . Тогда

д) Длину высоты находим как расстояние от точки до прямой , заданной общим уравнением :

.

е) Площадь треугольника находим по формуле: . Откуда .

Ответ: а) ; б) ; в) ;

г) ; д) ; е) .

7.1 – 30. Даны вершины пирамиды . Требуется найти:

а) длины ребер и ; б) угол между ребрами и ;

в) площадь грани ; г) объем пирамиды ;

д) уравнение плоскости грани ;

е) длину высоты пирамиды .

Решение.

а) Длины рёбер и находим как длины векторов и :

;

;

;

.

б) Угол между рёбрами и находим как угол между векторами и по формуле: . Учитывая, что: , , получим . Откуда

в) Площадь грани находим, используя геометрический смысл векторного произведения векторов, по формуле . Учитывая, что:

, , получим .

г) Объём пирамиды находим, используя геометрический смысл смешанного произведения векторов, по формуле . Учитывая, что:

,

,

получим .

д) Уравнение плоскости грани находим как уравнение плоскости, проходящей через точки , и , и записываем его в виде общего уравнения плоскости:

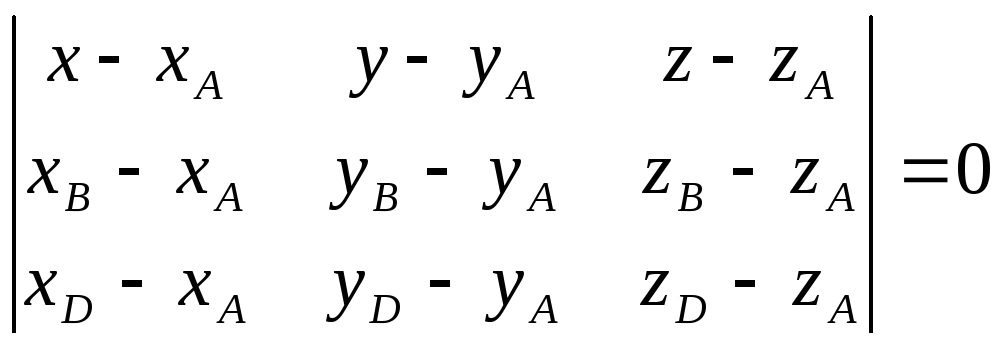
е) Длину высоты пирамиды находим как расстояние от точки до плоскости , заданной общим уравнением :

.

Ответ: а) , ; б) ; в) ;

г) ; д) ; е) .

8.1–30. Установить, какую кривую определяет алгебраическое уравнение второго порядка, построить её:

а) ; б) ;

в) .

Решение:

а) Выделяя полные квадраты в левой части уравнения , преобразуем его следующим образом:

.

Полученное уравнение определяет гиперболу с центром в точке и осями симметрии параллельными координатным осям. Для построения гиперболы в системе координат : 1) отмечаем центр гиперболы ; 2) проводим через центр пунктиром оси симметрии гиперболы; 3) строим пунктиром основной прямоугольник гиперболы с центром и сторонами и параллельными осям симметрии; 4) проводим через противоположные вершины основного прямоугольника пунктиром прямые, являющиеся асимптотами гиперболы, к которым неограниченно близко при бесконечном удалении от начала координат приближаются ветви гиперболы, не пересекая их; 5) изображаем сплошной линией ветви гиперболы (рис. 1).

Ответ: Гипербола с центром в точке (см. рис.1)..

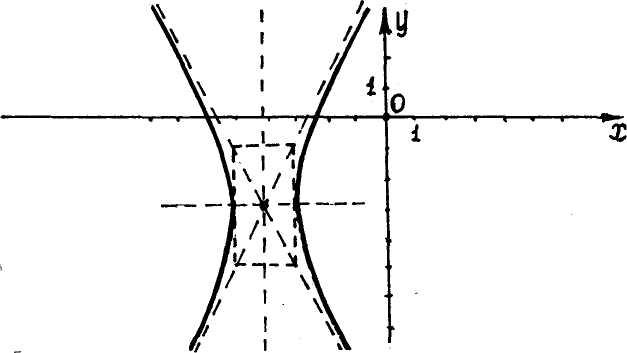
Рис.1

б) Выделяя полные квадраты в левой части

уравнения , преобразуем его следующим образом:

.

Полученное уравнение определяет эллипс с центром в точке и осями симметрии параллельными осям координат. Для построения эллипса в системе координат : 1) отмечаем центр эллипса ; 2) проводим через центр пунктиром оси симметрии эллипса; 3) строим пунктиром основной прямоугольник эллипса с центром и сторонами и параллельными осям симметрии; 4) изображаем сплошной линией эллипс, вписывая его в основной прямоугольник так, чтобы эллипс касался его сторон в точках пересечения прямоугольника с осями симметрии (рис.2).

Ответ: Эллипс с центром в точке (см. рис.2).

в). Выделяя полные квадраты в левой части уравнения , преобразуем его следующим образом:

Полученное уравнение определяет параболу с вершиной в точке и осью симметрии параллельной оси . Для построения параболы в системе координат : 1) отмечаем вершину параболы ; 2) проводим через вершину пунктиром ось симметрии параболы; 3) изображаем сплошной линией параболу, направляя её ветвь, с учётом того, что параметр параболы , в положительную сторону оси (рис.3).

Ответ: Парабола с вершиной в точке (см. рис.3).

Рис.2. Рис.3.

9.1-30. Требуется:

а) найти область определения функции ;

б) установить чётность (нечётность) функции .

Решение. а) Естественную область определения находим как множество всех значений аргумента функции, для которых формула имеет смысл: . Решив (на числовой прямой) систему неравенств , устанавливаем, что геометрическим образом множества является промежуток .

б) Находим сначала естественную область определения функции : . Решив (на числовой прямой) неравенство , устанавливаем, что геометрическим образом множества является объединение промежутков .

Так как область является симметричной относительно точки , то проверяем выполнение для всех условий: или , учитывая чётность и нечётность основных элементарных функций, входящих в аналитическое выражение .

Если область не симметрична относительно точки , то на этом множестве является функцией общего вида.

Для этого находим . Поскольку для всех , то функция является чётной.

Ответ: а) , ;

б) функция - чётная.

10.1-30. Вычислить пределы (не пользуясь правилом Лопиталя):

а) б) в) г) д)

Вычисление предела , где , начинают всегда с подстановки в предельного значения её аргумента . В результате могут получиться неопределённости , , , которые раскрывают тождественными преобразованиями такими, чтобы преобразованное выражение получилось определённым. При вычислении пределов используют свойства конечных пределов и бесконечно больших функций, а также следующие известные пределы: , , (), , , , , .

Решение. а) При подстановке вместо переменной её предельного значения получим неопределённость . Для её раскрытия сначала разделим числитель и знаменатель дроби на (старшую степень переменной в числителе и знаменателе), после чего используем свойства конечных пределов и бесконечно больших функций. Получим

.

б) При подстановке вместо переменной её предельного значения получим неопределённость . Для её раскрытия выделим в числителе и знаменателе дроби общий множитель вида , где - некоторое число, т.е. множитель . Затем сократим на него числитель и знаменатель дроби, после чего используем свойства пределов.

1) В квадратном трёхчлене множитель выделяют разложением квадратного трёхчлена по формуле , где . 2) В выражении множитель выделяют следующим способом:

.

В результате получим

.

в) При подстановке вместо переменной её предельного значения получим неопределённость . Выделим в числителе множители вида , где при и используем свойства пределов. Получим

Для раскрытия неопределённостей , содержащих тригонометрические и обратные тригонометрические функции, в числителе и знаменателе дроби выделяют сначала множители вида: ,, ,, где при , используя формулы тригонометрии: , , . После чего применяют свойства пределов, учитывая, что: , , , .

.

г)

Для раскрытия неопределённости , возникающей при вычислении предела , где , , сначала выражение представляют в виде , где при . После чего используют свойства пределов, заменяя выражение его предельным значением и учитывая, что =.

При подстановке вместо переменной её предельного значения получим неопределённость . Представим в виде , где при ,следующим способом:

=. Тогда учитывая, что ,, получим ==.

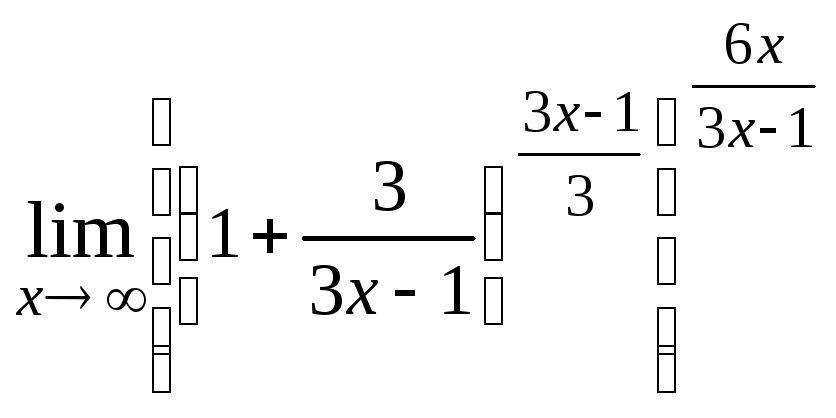
Ответ: а); б); в); г).

11.1-30. Для указанной функции требуется: а) выяснить при каких значениях параметра функция будет непрерывной; б) найти точки разрыва функции и исследовать их характер. Построить график функции.

а) ; б) .

Решение.

Точками разрыва функции являются точки разрыва функций в промежутках , ,…,, кроме того, точками возможного разрыва функции являются точки в окрестности которых и в самих точках функция задаётся разными аналитическими выражениями.

Точка является точкой непрерывности функции тогда и только тогда, когда: .

а) Поскольку функции и непрерывны в промежутках и как элементарные функции, определённые в каждой точке данных промежутков, то непрерывность функции может нарушиться только в точке её возможного разрыва .

Определяем значение параметра из условия непрерывности функции в точке : . Вычисляя , , : , , , из условия непрерывности , находим .

График непрерывной функции имеет вид изображённый на рис. 1.

б) Функции и непрерывны в промежутках и как элементарные функции, определённые в каждой точке данных промежутков, а функция в промежутке имеет точкой разрыва точку , в которой она не определена. Тогда для функции точка является точкой разрыва, а точки и , в окрестности которых и в самих точках функция задаётся разными аналитическими выражениями, являются точками возможного разрыва.

Исследуем на непрерывность точки :

1)

.

Следовательно, точка - точка разрыва 1-го рода функции .

2)

Следовательно, точка - точка бесконечного разрыва (2-го рода) функции .

3)

.

Следовательно, точка - точка непрерывности функции .

График функции имеет вид, изображённый на рис.2.

Ответ: а) Функция непрерывна при (рис.1); б) - точка разрыва 1-го рода, - точка бесконечного разрыва функции (рис.2).

Рис.1 Рис.2

12.1-30. Даны комплексные числа , , и алгебраическое уравнение . Требуется: а) вычислить, , ; б) представить комплексное число в тригонометрической форме, вычислить и результат представить в алгебраической форме; в) найти все корни алгебраического уравнения на множестве комплексных чисел.

Решение.

1а) Вычисляем : .

2а) Вычисляем .

Сначала находим (учитываем, что ). Тогда

3а) Вычисляем :

(учитываем, что ).

1б) Представляем комплексное число в тригонометрической форме , где

(так как комплексное число, изображается точкой , лежащей в третьем квадранте координатной плоскости). Тогда .

2б) Вычисляем по формуле Муавра:

. Полученный результат представляем в алгебраической форме: .

1в) Для нахождения корней алгебраического уравнения , раскладываем его левую часть на множители:

.

2в) Находим корни уравнения на множестве комплексных чисел, приравнивая каждый из множителей нулю (число корней, с учётом кратности, должно равняться порядку уравнения):

1) .

2) .

3) . Так как дискриминант квадратного уравнения , то уравнение имеет два комплексно-сопряжённых корня: .

Замечание. Корни , можно найти и как корни уравнения , по формуле . Для нахождения комплексных значений корня, число следует представить в виде комплексного числа в тригонометрической форме: , после чего значения корня найти по формуле: ,где

Ответ: a) , , ;

б) ; в) , , .