
- •Введение
- •Глава 1. Функции и пределы § 1. Функции и их свойства
- •§ 2. Предел функции и его свойства
- •§3. Замечательные пределы
- •§ 4. Бесконечно малые величины
- •§ 5. Непрерывность функций
- •Глава II. Дифференциальное исчисление § 1. Производная. Основные правила дифференцирования функций
- •§ 2. Дифференциал функции
- •§ 3. Производные и дифференциалы высших порядков
- •§ 4. Основные теоремы дифференциального исчисления
- •§ 5. Правило Лопиталя
- •Глава III. Применение производных к исследованию функций и построению их графиков § 1. Исследование функции на монотонность и экстремумы
- •§ 2. Исследование функции на выпуклость, вогнутость и точки перегиба ее графика
- •§ 3. Асимптоты
- •§ 4. Схема полного исследования функции
- •Глава IV. Неопределенный интеграл § 1. Понятие первообразной и неопределённого интеграла. Основная таблица интегралов
- •Основные свойства интеграла
- •Основная таблица интегралов
- •§ 2. Основные методы интегрирования
- •§ 3. Интегрирование рациональных дробей
- •§ 4. Интегрирование некоторых видов тригонометрических выражений
- •§ 5. Интегрирование некоторых видов иррациональных выражений
- •Библиографический список Основные учебные и справочные издания
- •Дополнительные учебные и справочные издания
- •Оглавление
§ 4. Основные теоремы дифференциального исчисления
Теорема Роля (о корнях производной)
Если функция
![]() непрерывна на отрезке
непрерывна на отрезке
![]() ,
дифференцируема во всех его внутренних
точках и имеет на концах отрезка равные
значения
,
дифференцируема во всех его внутренних
точках и имеет на концах отрезка равные
значения
![]() ,
то внутри отрезка существует хотя бы
одно значение
,
то внутри отрезка существует хотя бы
одно значение
![]() ,
в
которой
производная обращается в нуль, т.е.
,
в
которой
производная обращается в нуль, т.е.
![]() .
.
Геометрическая интерпретация теоремы Роля:
Н а
дуге
а
дуге
![]() графика функции
графика функции![]() ,
удовлетворяющей условиям теоремы Ролля,
найдется точка М,
в которой касательная ТК
параллельна хорде АВ
и оси ОХ.
Таких точек может быть и несколько.
,
удовлетворяющей условиям теоремы Ролля,
найдется точка М,
в которой касательная ТК
параллельна хорде АВ
и оси ОХ.
Таких точек может быть и несколько.
Теорема Лагранжа (о конечном приращении функции)
Если функция
![]() непрерывна на отрезке
непрерывна на отрезке![]() и дифференцируема во всех его внутренних
точках, то внутри отрезка существует
хотя бы одно значение
и дифференцируема во всех его внутренних
точках, то внутри отрезка существует
хотя бы одно значение
![]() ,
для которого:
,
для которого:
![]()
Из теоремы следует формула конечных приращений:
![]()
т.е. приращение функции на интервале равно произведению производной в некоторой промежуточной точке интервала не приращение независимой переменой.
Теорема Коши (об отношении приращений двух функций)
Если функции![]() и
и
![]() непрерывны на отрезке
непрерывны на отрезке
![]() и дифференцируемы во всех его внутренних
точках, причем
и дифференцируемы во всех его внутренних
точках, причем
![]() внутри
отрезка, то найдется хотя бы одна
внутренняя точка
внутри
отрезка, то найдется хотя бы одна
внутренняя точка
![]() ,
для которой:
,
для которой:
 .
.
§ 5. Правило Лопиталя
Теорема 1
(правило Лопиталя для раскрытия
неопределенностей вида![]() )
)
Пусть функции
![]() на некотором отрезке
на некотором отрезке
![]() удовлетворяют условиям теоремы Коши
и обращаются в нуль при
удовлетворяют условиям теоремы Коши
и обращаются в нуль при
![]() ,
т. е.
,
т. е.
![]() .
Тогда, если существует предел отношения
производных
.
Тогда, если существует предел отношения
производных
![]() при
при
![]() ,
то существует и предел отношения функций
,
то существует и предел отношения функций
![]() ,
причем они равны друг другу:
,
причем они равны друг другу:
![]() .
.
Теорема имеет
место и в том случае, если функции
![]() не определены при х
= а,
но
не определены при х
= а,
но
![]()
Если
![]() ,
а производные
,
а производные
![]() удовлетворяют условиям, налагаемым на
удовлетворяют условиям, налагаемым на
![]() теоремой 1, правило Лопиталя применяется
повторно уже к отношению производных
теоремой 1, правило Лопиталя применяется
повторно уже к отношению производных
![]() .
Получим:
.
Получим:
![]()
Правило Лопиталя
применяется и в том случае, когда![]() а
а
![]()
Правило Лопиталя
остается в силе, если окажется, что
![]() .
.
Примеры
![]()
![]()

Теорема 2
(правило Лопиталя для раскрытия
неопределенностей вида
![]() )
)
Пусть функции
![]() непрерывны и дифференцируемы при всех
непрерывны и дифференцируемы при всех
![]() в окрестности точки
в окрестности точки![]() ,
причем
,
причем
![]() ;
пусть далее
;
пусть далее
![]() .
Тогда, если существует предел
.
Тогда, если существует предел
![]() то существует и предел
то существует и предел
![]() ,
и они равны между собой:
,
и они равны между собой:
![]() .
.
Данное правило
допускает повторное применение, а также
сохраняет силу в случаях, когда
![]() или
когда
или
когда
![]() .
.
Примеры
![]() .
.
![]()
![]()
С помощью правил
Лопиталя раскрываются неопределенности
![]() которые различными преобразованиями
сводятся к неопределенностям видов
которые различными преобразованиями
сводятся к неопределенностям видов
![]() или
или
![]() .
.
Примеры



Глава III. Применение производных к исследованию функций и построению их графиков § 1. Исследование функции на монотонность и экстремумы
Теорема (необходимый признак монотонности)
Пусть функция
![]() на отрезке
на отрезке
![]() имеет
производную. Тогда:
имеет
производную. Тогда:
1. Если
![]() не убывает на
не убывает на
![]() ,
то
,
то
![]() на отрезке
на отрезке
![]() .
.
2. Если
![]() не возрастает на
не возрастает на
![]() ,
то
,
то
![]() на отрезке
на отрезке
![]() .
.
3. Если функция
![]() =
const
на
=
const
на
![]() ,
то
,
то![]() на отрезке
на отрезке
![]() .
.
Теорема (достаточный признак монотонности)
Пусть функция
![]() непрерывна
и дифференцируема на отрезке
непрерывна
и дифференцируема на отрезке
![]() .
Тогда:
.
Тогда:
1. Если
![]() на отрезке
на отрезке
![]() ,
то
,
то
![]() не убывает на отрезке
не убывает на отрезке
![]() .
.
2. Если
![]() на отрезке
на отрезке
![]() ,
то
,
то
![]() не возрастает на отрезке
не возрастает на отрезке
![]() .
.
3. Если
![]() на отрезке
на отрезке
![]() ,
то
,
то
![]() =
const
на
=
const
на
![]() .
.
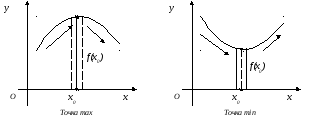
Точка
![]() называется: точкой
максимума
функции
называется: точкой
максимума
функции
![]() ,
если
,
если
![]() в некоторой окрестности точки
в некоторой окрестности точки![]() .
Точка
.
Точка
![]() называется точкой
минимума функции
называется точкой
минимума функции![]() ,
если
,
если
![]() в некоторой окрестности точки
в некоторой окрестности точки
![]() .
Точки минимума и максимума называются
точками
экстремума,
а значения функции в них – экстремальными
значениями.
Точки экстремумов разделяют интервалы
монотонности.
.
Точки минимума и максимума называются
точками
экстремума,
а значения функции в них – экстремальными
значениями.
Точки экстремумов разделяют интервалы
монотонности.
Теорема (необходимый признак существования экстремума)
Если
в точке
![]() функция
функция
![]() достигает экстремума, то ее производная
в этой точке либо равна нулю, либо не
существует.
достигает экстремума, то ее производная
в этой точке либо равна нулю, либо не
существует.
Точки, в которых производная равна нулю, называются стационарными точками I рода; стационарные точки и точки, где производная не существует, вместе называются критическими точками I рода.
Теорема (первый достаточный признак существования точки экстремума)
Пусть
функция
![]() непрерывной
в некоторой окрестности точки
непрерывной
в некоторой окрестности точки
![]() и
дифференцируема в ней (за исключением,
быть может, самой точки
и
дифференцируема в ней (за исключением,
быть может, самой точки
![]() ).
Если при переходе через
точку
).
Если при переходе через
точку
![]() производная
производная
![]() меняет
знак с плюса на минус,
то
меняет
знак с плюса на минус,
то
![]() –
точка
максимума,
если с минуса на плюс,
то
–
точка
максимума,
если с минуса на плюс,
то
![]() –
точка
минимума,
если знак производной не меняется, то
функция не имеет в точке
–
точка
минимума,
если знак производной не меняется, то
функция не имеет в точке
![]() экстреума.
экстреума.
Пример
Исследовать на
экстремум функцию
![]()
Решение:
1. Ищем область
определения:
![]()
2. Ищем
![]()
3. Ищем критические точки:
![]()
![]() существует
на всей области определения, поэтому
других критических точек нет.
существует
на всей области определения, поэтому
других критических точек нет.
4. Исследуем знаки
![]() до
и после критических точек:
до
и после критических точек:

5. Определяем
экстремальные точки по смене знака
![]() и
вычисляем экстремальные значения
функции:
и
вычисляем экстремальные значения
функции:

Теорема (второй достаточный признак существования экстремума)
Точка
![]() есть
точка экстремума функции
есть
точка экстремума функции
![]() ,
если
,
если
![]() ,
,
![]() ,
причем
если
,
причем
если
![]() ,
то
,
то
![]() – точка
минимума,
а если
– точка
минимума,
а если
![]() ,
то
,
то
![]() –
точка
максимума.
–
точка
максимума.
Пример
В предыдущем
примере
![]()

Наибольшее и наименьшее значения функции на отрезке
Для
отыскания наибольшего
![]() и
наименьшего
и
наименьшего![]() значений функции
на отрезке
значений функции
на отрезке
![]() ,
надо найти все экстремальные значения
функции внутри отрезка и
значения функции на концах отрезка.
Из
всех вычисленных значений функции
выбрать наибольшее и наименьшее:
,
надо найти все экстремальные значения
функции внутри отрезка и
значения функции на концах отрезка.
Из
всех вычисленных значений функции
выбрать наибольшее и наименьшее:
![]()
Пример
Найти наибольшее
и наименьшее значение функции
![]() (см. предыдущие примеры) на отрезке
(см. предыдущие примеры) на отрезке
![]()

