Дешифратор. Виды дешифраторов
Дешифраторы
Дешифратором называется устройство комбинаторного типа, имеющего m-входов и n –выходов
Число выходов полного дешифратора n = 2m. Дешифраторы преображают двоичный код в десятичный и в унитарный код. Унитарный код имеет в своем составе только одну логическую единицу и она соответствует десятичной цифре двоичного кода.
Дешифратор описывается системой уравнений следующего вида:
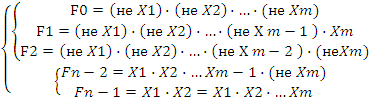
Каждое уравнение дешифратора соответствует конъюнкции совершенной дизъюнктивной нормальной формы.
Дешифратор на 2 входа
Он имеет вид следующей таблицы истинности
СДНФ
f0=(не Х1∙неХ2)
f1=(не Х1)∙Х2
f2=X1∙(неX2)
f3=X1∙Х2
Таблица 3.2
|
X1 |
X2 |
f0 |
f1 |
f2 |
f3 |
|
0 |
0 |
1 |
0 |
0 |
0 |
|
0 |
1 |
0 |
1 |
0 |
0 |
|
1 |
0 |
0 |
0 |
1 |
0 |
|
1 |
1 |
0 |
0 |
0 |
1 |
{И,НЕ}
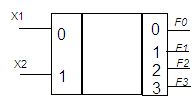
Рис. 3.6
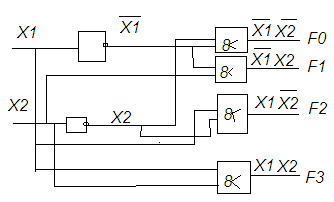
Рис. 3.7
Дешифратор в линейном базисе {ИЛИ,НЕ}
{f0=(
1)
(
2)
{f1=(
1)∙х2
{f2=x1∙(
2)
{f3=x1∙x2
Чтобы построить дешифратор в базисе {ИЛИ,НЕ}, нужно преобразовать уравнение к этому базису, заменив все конъюнкции стрелками Пирса.
Переходим к уравнению:
f0=
f1=
→
f2=
f3=
|
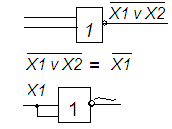
X1 |
X2 |
X3 |
|
0 |
0 |
0 |
|
0 |
0 |
1 |
|
0 |
1 |
0 |
|
0 |
1 |
1 |
|
0 |
0 |
0 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |
|
1 |
1 |
1 |
(рис.схемы и диаграммы вставить)
Из диаграммы видно, что в каждый момент времени истинен только один выходной сигнал.
Если подавать на вход периодический сигнал, то используя дешифратор, можно осуществить деление частоты и суммировать скважность входных/выходных сигналов.
C=∙
100%
Под линейным дешифратором понимается дешифратор, имеющий 1 каскад по реализации функций. На каждом элементе этого дешифратора имеются все входные сигналы. Время преобразования информации (быстродействие дешифратора) определятся, как =cp+cp.инв.
cp.инв- среднее время инвертирования сигнала.
Поэтому линейный дешифратор обладает наибольшим быстродействием, однако, с увеличением числа входных переменных из-за ограничения величины коэффициента объединения по входу становится невозможным его реализация.
С целью получения более сложных схем используются многокаскадные дешифраторы.
Прямоугольные и пирамидальные дешифраторы
Пирамидальные дешифраторы строятся обычных на двухходовых элементах, где число входных переменных больше двух. Дешифратор наращивается каскадно, путем добавления в дешифратор дополнительных каскадов.
Пирамидальный дешифратор для трех переменных:
f0=
1∙
2∙
3
f1=
1∙
2∙
х3
…
f7=x1∙x2∙x3
Используя базис {и,не}, построим схему (рис.4.1).
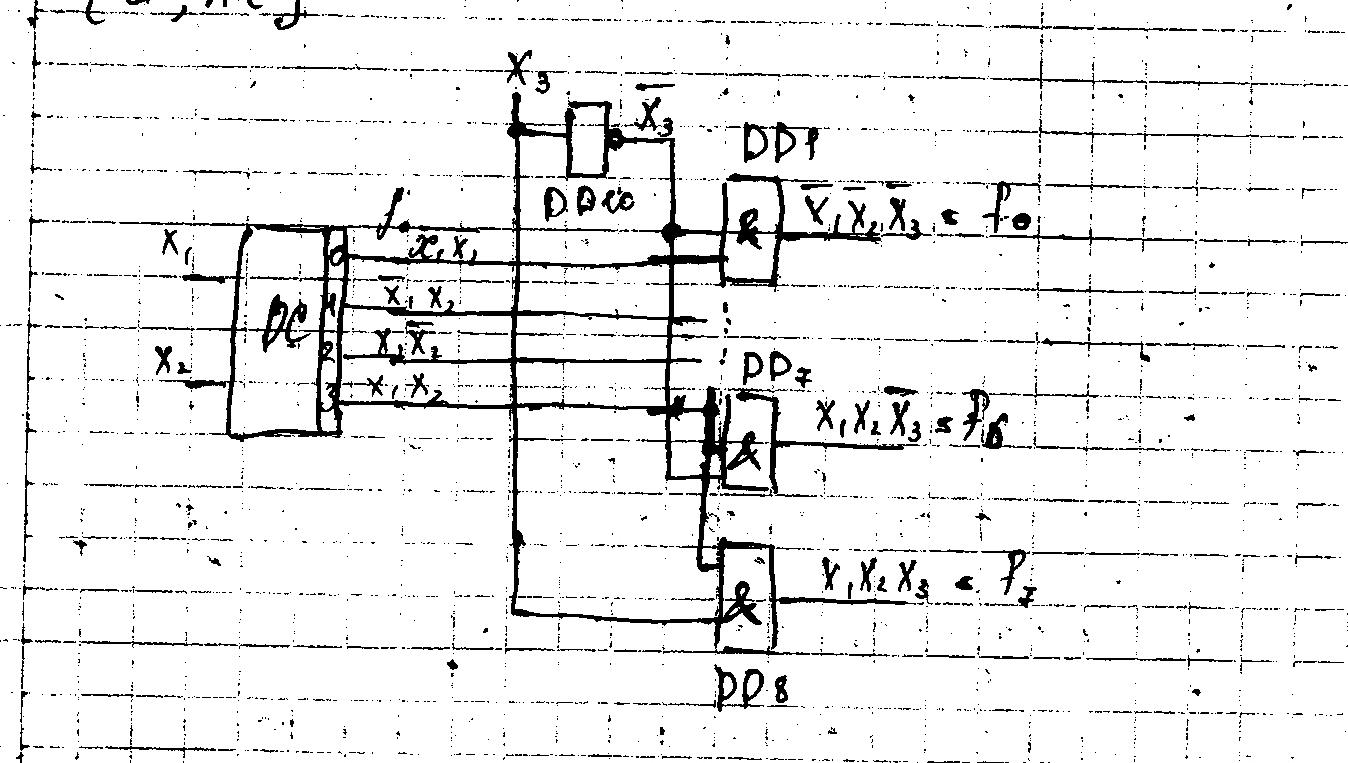
Рис.4.1
Число каскадов пирамидальных дешифраторов = (m-1). На каждом каскаде задается сигнал и с учётом инверсий время дешифрирования тогда определяется tpc=(m-1) cр+ср.инв. .
Отсюда видно, что при увеличении числа каскадов быстродействие уменьшается на число каскадов. Это главный недостаток в пирамидальном дешифраторе по сравнению с линейным.
Для получения сравнительных характеристик используется пирамидальные дешифраторы. Пирамидальные дешифраторы строятся на основе линейных путем разделения переменных почти пополам.
f0=
1∙
2∙
3∙
4∙
5
f1=
1∙
2∙
3∙
4∙
х5
…
f31=x1∙ х2∙х3∙ x4∙ х5
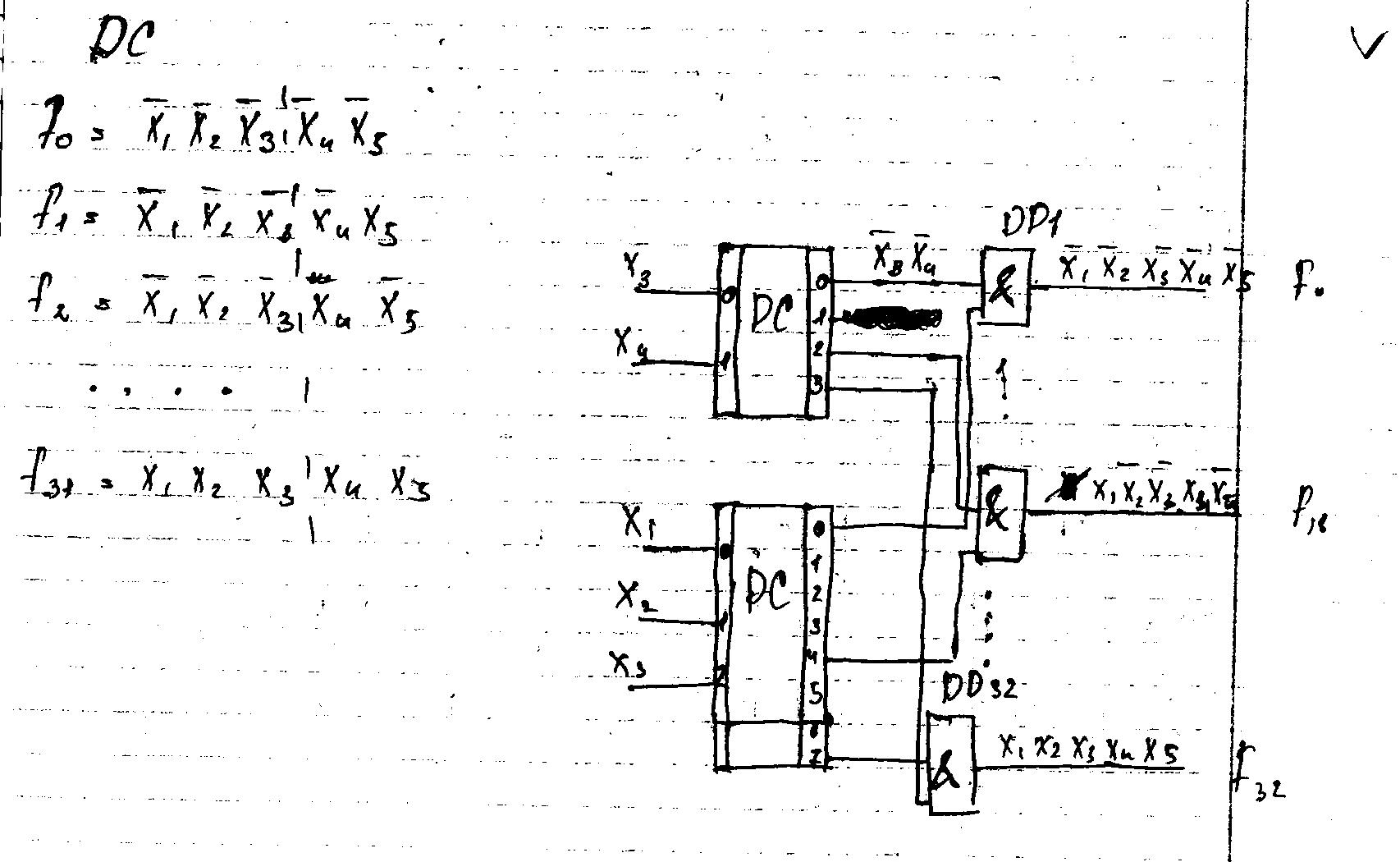
Рис.4.2
Дешифратор на 5 входов строится из 2 дешифраторов линейных: на 2 и на 3 входа, при этом быстродействие ухудшается примерно на величину ср и коэффициент объединения на входе превышает 3.
Дешифраторы используются для преобразования 2-го входа адреса доступного по шине адреса ША. Если ША 32-ух разрядная, то в этом случае необходим дешифратор с 32-мя входами, который может обратится к 232 ячейкам памяти