10. Необходимый признак сходимости числовых рядов. Свойства сходящихся рядов.

При исследовании рядов наиболее важным является вопрос о сходимости (установление факта сходимости и расходимости). Для этого используют признак сходимсоти.

Теорема 1: Необходимый признак сходимости рядов. Если ряд - сходится, то предел его общего члена Un при n равен нулю: Un =0

Следствие: Если Un 0 , то ряд расходится.

Свойства сходимости рядов:

Теорема 1: если ряд сходится и его сумма равна S, то сходится и ряд (где a=const). Его сумма S₁ = a*S

Теорема 2: если 2 ряда U1+U2+…+Un=

V1+V2+…-Vn+…=

Сходятся и их суммы соответственно равны S₁ и S₂, то также сходится и ряд составленного из суммы разности исходных рядов, т.е. ряды ; - также сходятся. (S₁+S₂) или (S₁-S₂).

10. Признаки сравнения знакоположительных числовых рядов. Первый и второй признак сравнения.

Пусть заданы законоположительные числовые ряды Un>0, Vn>0,

U1+U2+…+Un+…= (*)

V1+V2+…+Vn+…= (**)

1. Первый признак сравнения.

Если для членов ряда (*) и (**) выполняется условие UnVn , то

а) если ряд (**) сходится, то сходится и ряд (*)

б) если ряд (*) расходится, то расходится и ряд (**)

2. Второй признак сравнения.

Если для членов ряда (*) и (**) существует отличный от нуля предел

=A, A, 0<A<, то оба ряда сходятся или расходятся одновременно.

В качестве эталонов, при использовании признаков сравнения применяют:

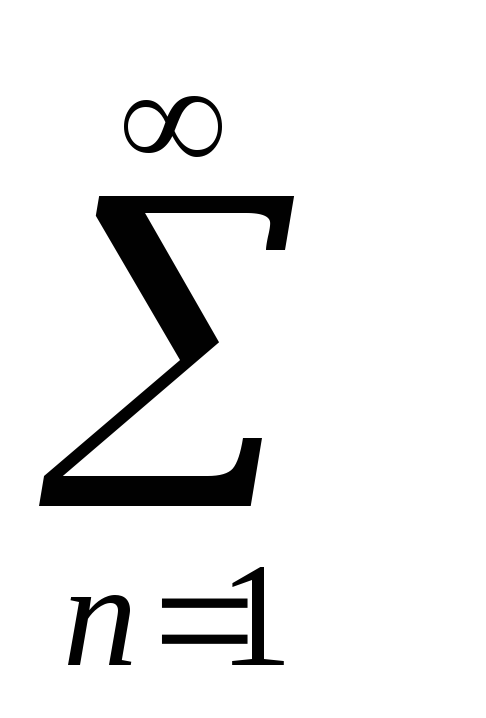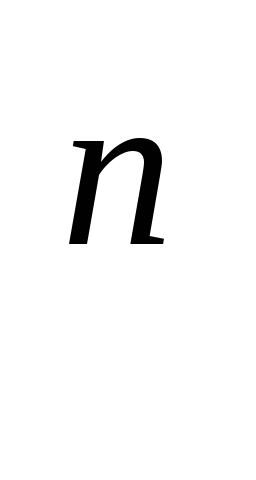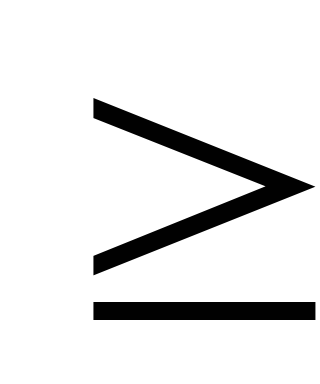• Геометрическую прогрессию bq - сходится при |q|<1, расходится при |q|1

• Обобщенный гармонический ряд 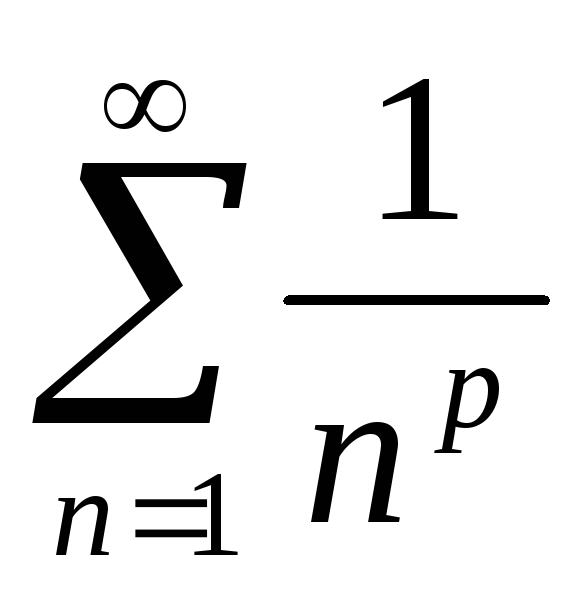- сходится при p>1, расходится при p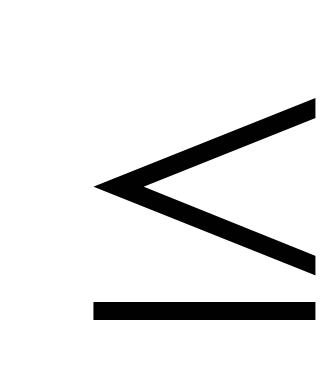1

10. Интегральный признак Коши.

Пусть члены ряда U1+U2+…+Un+…= неотрицательны и ряд невозрастающий: U1

Если существует невозрастающая, непрерывная функция f(x), с областью определения x[1;+), такая, что f(1)=U1, f(2)=U2,…, f(n)=Un,…, то ряд сходится или расходится одновременно с несобственным интегралом .

Замечание: Несобственный интеграл называется сходящимся, если существует конечный предел вида = .

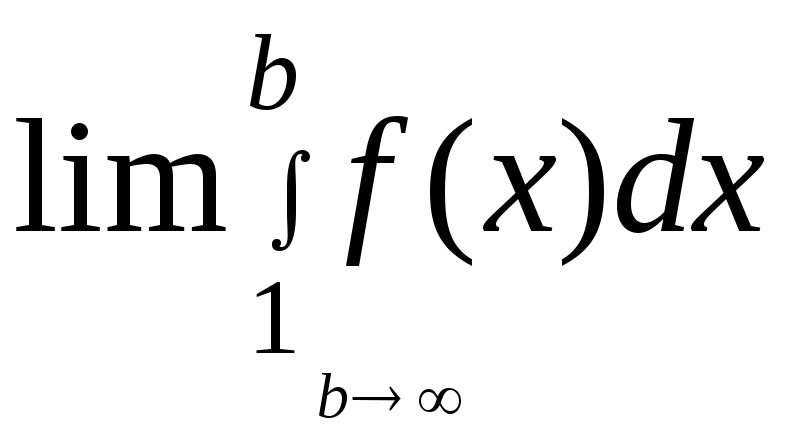10. Признак Даламбера.

Если члены ряда U1+U2+…+Un+…= - строго положительны и существует предел = l , то l<1 ряд сходится,

l>1 ряд расходится,

l = 1 признак ответа не дает.

10. Сходимость обобщенного гармонического ряда 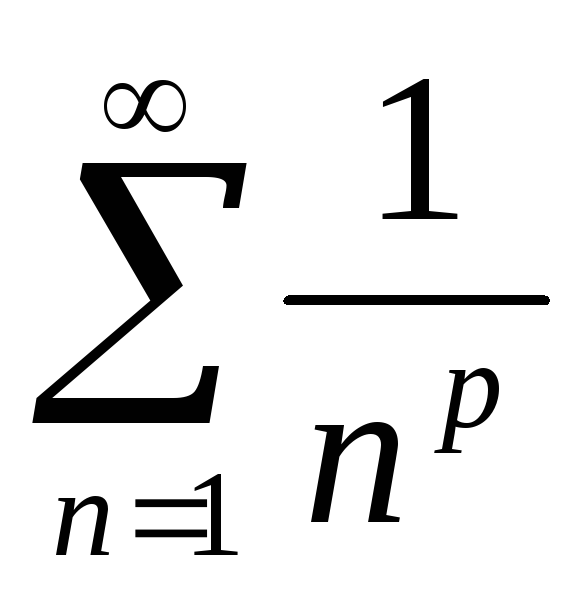. Используя интегральный признак Коши доказать, что при p=2 ряд сходится.

10. Знакочередующиеся числовые ряды (определение, примеры). Признак Лейбница.

Определение: Ряд называется законопеременным, если среди его членов есть как положительные, так и отрицательные величины.

Ряд называется законочередубщимся, если в нем происходит чередование знаков (+-)

Пример: = 1-1/2+1/3-1/4+… - законочередующийся ряд

Рассмотрим законочередующиеся ряды, они также могут сходиться или расходиться.

Для установления факта сходимости законочередующихся рядов используют теорему (признак) Лейбница.

Признак Лейбница: Если в законочередующихся рядах , где Un>0, члены таковы, что: 1) U1>U2>U3…>Un>… ; 2) Un = 0 => такой ряд сходится, а его сумма не превышает 1ого члена U1.